Cho số nguyên n ≥ 3. Trong không gian cho n điểm mà không có 3 điểm nào thẳng hàng và không có 4 điểm nào đồng phẳng. Tại mỗi điểm ghi 1 số nguyên dương sao cho không có 2 điểm nào được ghi bởi cùng 1 số và n số được ghi là n số nguyên dương đầu tiên. Gọi điểm được ghi số i là điểm i. Nối tất cả các cặp điểm (p, q) với p < q bởi 1 mũi tên từ p đến q. Tô mỗi mũi tên bởi 1 trong 2 màu xanh, đỏ. Một cách tô màu được gọi là "tốt"nếu tồn tại 2 điểm j, k sao cho có thể đi từ j đến k qua các mũi tên xanh và cũng có thể đi từ j đến k qua các mũi tên đỏ. Hỏi có tất cả bao nhiêu cách tô màu "tốt"?

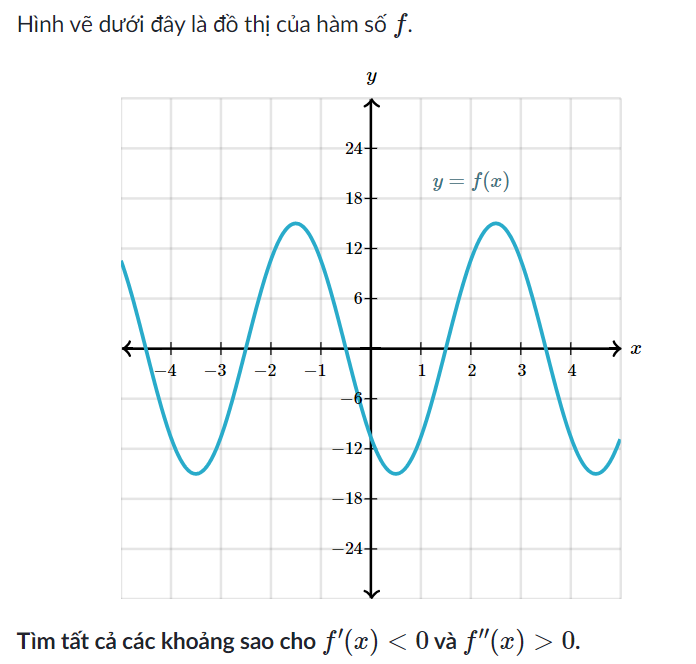
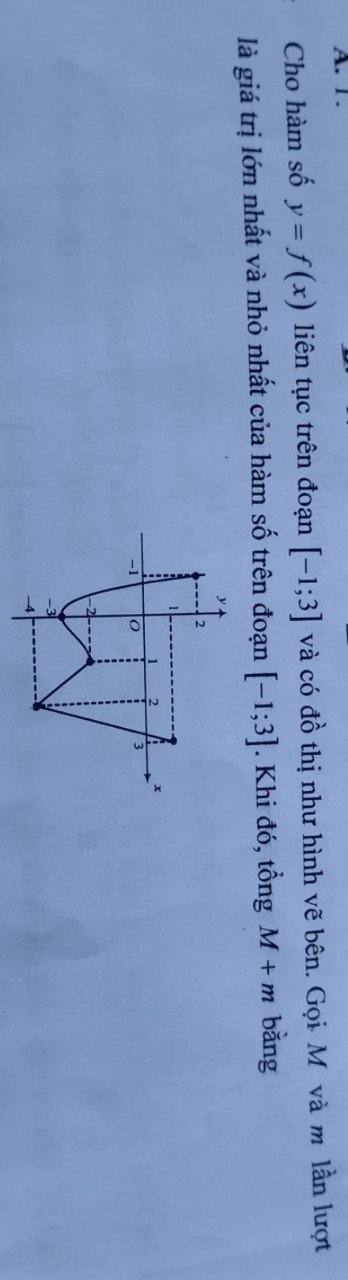
khó quá
Khó thì để cho người khác còn làm !