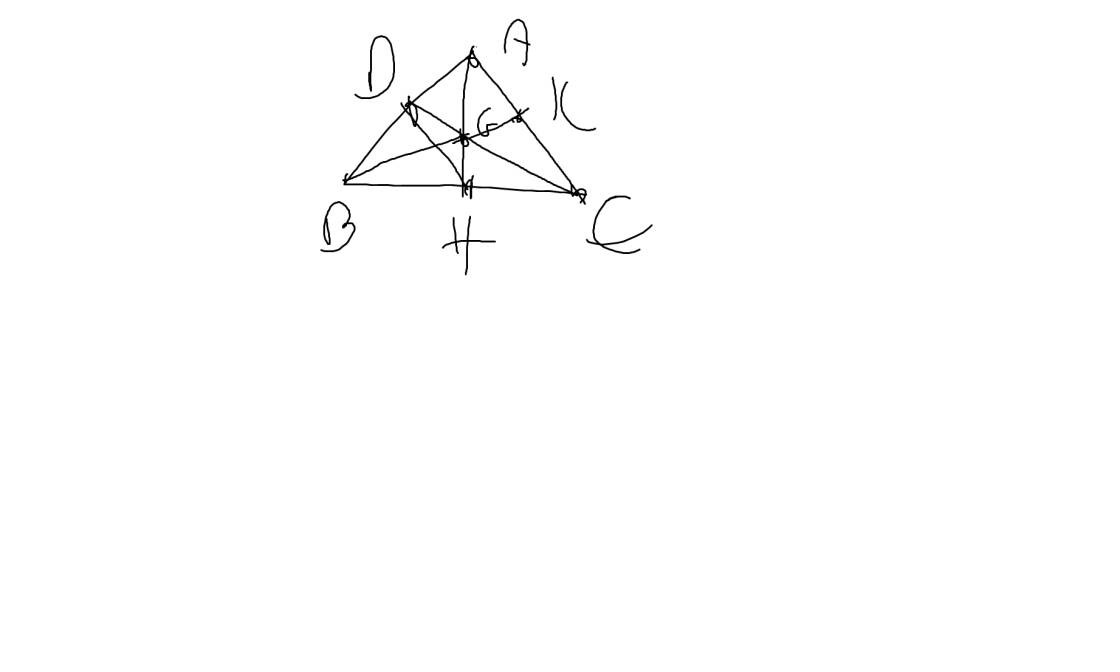
Bài 6. Cho tam giác ABC có AB = AC. kẻ AH vuông góc với BC (H∈ BC)
Từ H kẻ đường thẳng song song với AC, cắt AB tại D.
a) Chứng minh ∆ADH là tam giác cân
b) Gọi G là giao của CD và AH. Chứng minh G là trọng tâm ∆AВС
c) Chứng minh AB + AC +BC > AH + 3BG
*Lưu ý: Gồm cả hình vẽ

a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
=>\(\widehat{HAB}=\widehat{HAC}\)
mà \(\widehat{DHA}=\widehat{HAC}\)(DH//AC)
nên \(\widehat{DHA}=\widehat{DAH}\)
=>ΔDAH cân tại D
b: Ta có: \(\widehat{DHA}+\widehat{DHB}=90^0\)
\(\widehat{DAH}+\widehat{DBH}=90^0\)
mà \(\widehat{DHA}=\widehat{DAH}\)(ΔDAH cân tại D)
nên \(\widehat{DHB}=\widehat{DBH}\)
=>DH=DB
=>DA=DB
=>D là trung điểm của AB
Xét ΔABC có
AH,CD là các đường trung tuyến
AH cắt CD tại G
Do đó: G là trọng tâm của ΔABC
c: Xét ΔABC có
G là trọng tâm
Do đó: BG cắt AC tại trung điểm K của AC
TA có:
mà AB=AC
nên AD=DB=AK=KC
Xét ΔDBC và ΔKCB có
DB=KC
BC chung
Do đó: ΔDBC=ΔKCB
=>DC=BK
Xét ΔBAC có
G là trọng tâm
BK là đường trung tuyến
Do đó:
=>2BK=3BG
Trên tia đối của tia KB, lấy E sao cho KB=KE
Xét ΔKAE và ΔKCB có
KA=KC
(hai góc đối đỉnh)
KE=KB
Do đó: ΔKAE=ΔKCB
=>AE=CB
AH+3BG=AH+2BK=AH+BE<AB+BE<(AB+AE+AB)=AB+AC+BC