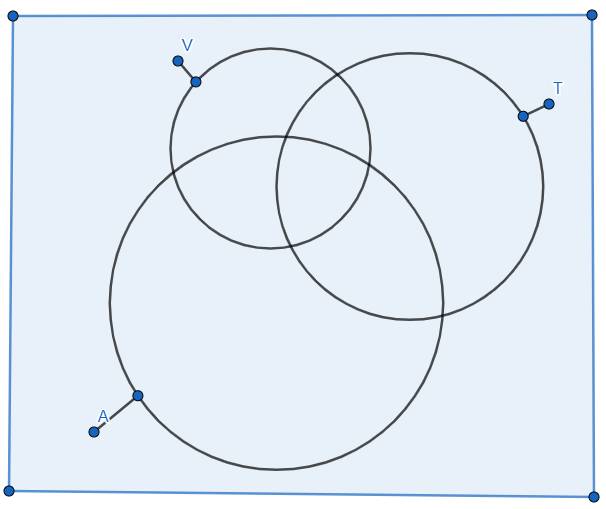
Gọi V, T, A lần lượt là tập hợp các học sinh giỏi Văn, Toán, Tiếng Anh. Theo đề bài, ta có: \(\left|V\right|=18;\left|T\right|=20;\left|A\right|=22\)\(;\left|V\cap T\cap A\right|=5\)\(;\left|A\cup T\cup V\right|=34\)

Áp dụng công thức bù trừ, ta có:

\(\left|V\cup T\cup A\right|=\left|V\right|+\left|T\right|+\left|A\right|-\left|V\cap T\right|-\left|T\cap A\right|-\left|A\cap V\right|+\left|V\cap T\cap A\right|\)

\(\Rightarrow34=18+20+22-P+5\) (với \(P=\left|V\cap T\right|+\left|T\cap A\right|+\left|A\cap V\right|\))

\(\Rightarrow P=31\)

Số học sinh thích đúng 1 môn trong 3 môn Toán, Văn, Tiếng Anh chính bằng:

\(\left|V\cup T\cup A\right|-P+2\left|V\cap T\cap A\right|\) \(=34-31+2.5=13\) (học sinh)

22 cách chọn

10x8x6=480

\(\overline{abc}\) là số cần tìm

số cách chọn c là: 5 

Số cách chọn b là 5

Số cách chọn a là: 9

Vậy Số số lẻ thỏa mãn đk đề bài là: 5 x 5 x 9 =225 số

Hàng của chữ số khác 0 đầu tiên bên trái của d = 1000 là hàng nghìn.Quy tròn a đền hàng chục nghìn ta được 54920000.

 Hàng của chữ số khác 0 đầu tiên bên trái của d = 0,002 là hàng phần nghìn.

Quy tròn b đền hàng phần trăm ta được 5,79.

a) Sai số tuyệt đối ∆ = |2,718281828459 – 2,7| = 0,018281828459 < 0,02.

Sai số tương đối 

δ=Δ|2,7|=0,0182818284592,7≈0,68%< 0,75%.

b) Quy tròn e đến hàng phần nghìn ta được số gần đúng là 2,718.

c) Hàng của chữ số khác 0 đầu tiên bên trái của độ chính xác d = 0,00002 là hàng phần trăm nghìn. Quy tròn e đến hàng phần trăm nghìn ta được số gần đúng của e là 2,71828.

a) Sai số tuyệt đối ∆ = |2,718281828459 – 2,7| = 0,018281828459 < 0,02.

Sai số tương đối 

δ=Δ:|2,7|=0,018281828459 : 2,7≈

0,68% < 0,75%.

b) Quy tròn e đến hàng phần nghìn ta được số gần đúng là 2,718.

c) Hàng của chữ số khác 0 đầu tiên bên trái của độ chính xác d = 0,00002 là hàng phần trăm nghìn. Quy tròn e đến hàng phần trăm nghìn ta được số gần đúng của e là 2,71828.

Gọi D, E lần lượt là giao điểm của đường biên \(x+2y\ge2\) với 2 trục Ox, Oy

\(\Rightarrow D\left(2;0\right)\) và \(E\left(0;1\right)\Rightarrow\left\{{}\begin{matrix}OD=2\\OE=1\end{matrix}\right.\)

\(\Rightarrow S_{ODE}=\dfrac{1}{2}.2.1=1\)

\(S_{ABCO}-S_{ODE}=2022\Leftrightarrow a^2-1=2022\)

\(\Rightarrow a^2=2023\Rightarrow a\approx44,98\)

A là đáp án đúng

chọn A

ĐKXĐ: \(\left\{{}\begin{matrix}9y-5\ge0\\x+y\ge0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y\ge\dfrac{5}{9}\\x+y\ge0\end{matrix}\right.\).

Phương trình (1) tương đương với: 

\(\left(x^2+y^2\right)\left(x+y\right)-\left(x+y\right)+2xy=0\)

\(\Leftrightarrow\left(x^2+y^2\right)\left(x+y\right)-\left(x^2+y^2\right)+x^2+y^2-\left(x+y\right)+2xy=0\)

\(\Leftrightarrow\left(x^2+y^2\right)\left(x+y-1\right)+\left(x+y\right)^2-\left(x+y\right)=0\)

\(\Leftrightarrow\left(x^2+y^2\right)\left(x+y-1\right)+\left(x+y\right)\left(x+y-1\right)=0\)

\(\Leftrightarrow\left(x+y-1\right)\left(x^2+y^2+x+y\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x+y-1=0\\x^2+y^2+x+y=0\end{matrix}\right.\)

- Với \(x^2+y^2+x+y=0\) có \(x+y=0\) (theo điều kiện) 

suy ra \(x=y=0\) (không thỏa mãn).

- Với \(x+y-1=0\Leftrightarrow y=1-x\) thế vào phương trình (2) ta được: 

\(x^2+11x+6=2\sqrt{9\left(1-x\right)-5}+\sqrt{1}\)

\(\Leftrightarrow x^2+11x+5-2\sqrt{14-9x}=0\)

\(\Rightarrow\left(x^2+11x+5\right)^2=4\left(14-9x\right)\)

\(\Leftrightarrow x^4+22x^3+131x^2+146x-31=0\)

Bạn giải phương trình trên, thử lại ta được nghiệm của bài toán. 

Đáp án ra số khá xấu nên thầy không ghi ra đây. 

Em có thể tham khảo cách làm nhé.