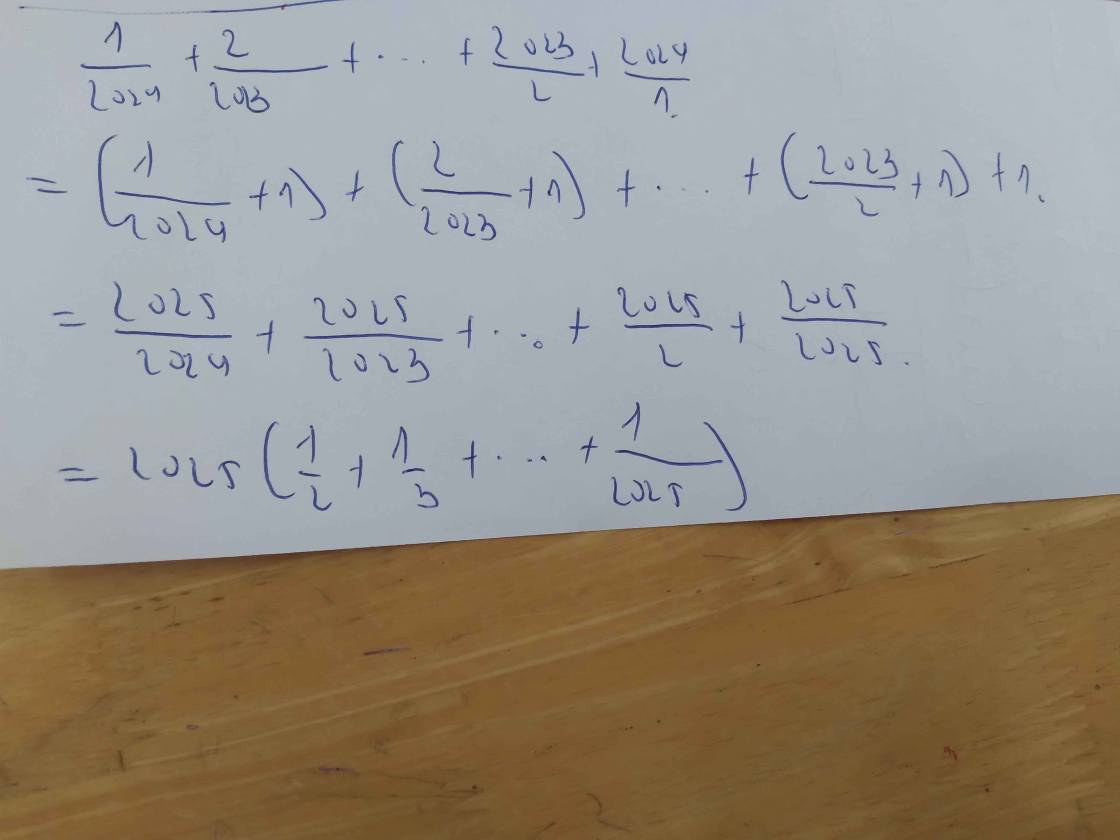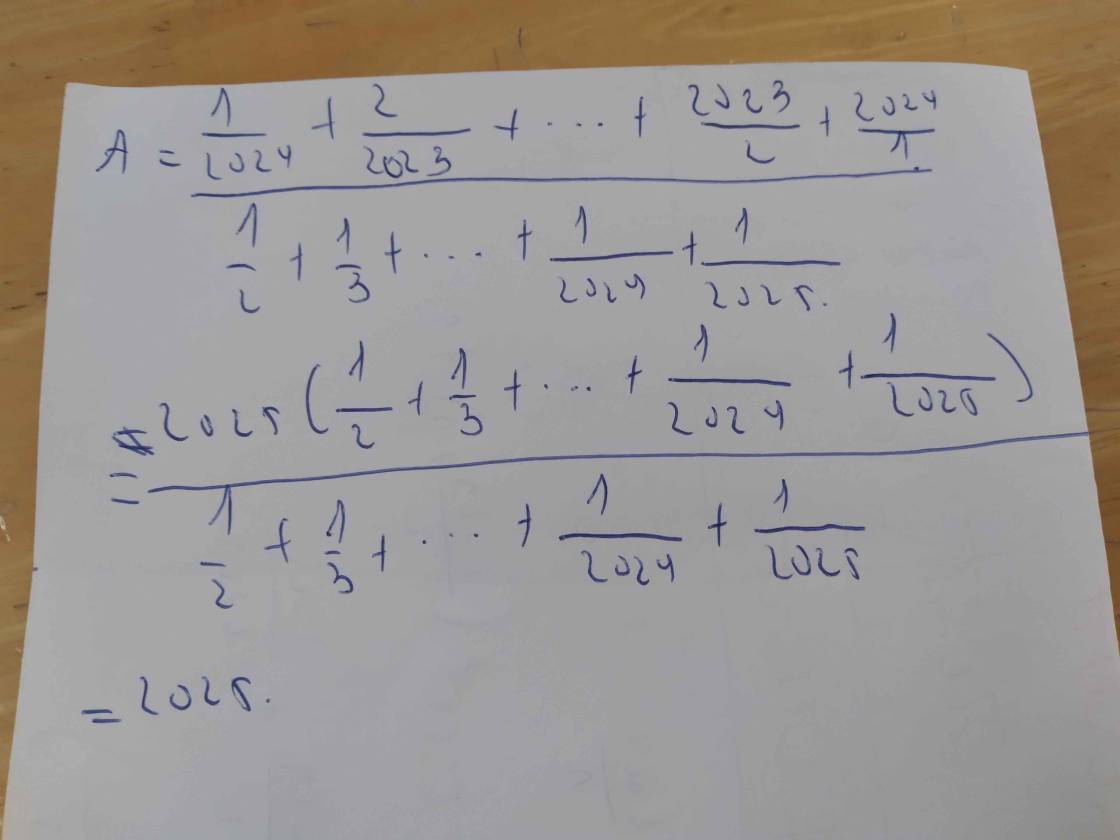Đề bài không đầy đủ. Bạn xem lại.

a) \(S=1+2+2^2+...+2^{2022}\)

\(2S=2+2^2+...+2^{2023}\)

\(2S-S=\left(2+2^2+...+2^{2023}\right)-\left(1+2+...+2^{2022}\right)\)

\(S=2^{2023}-1\)

Giả sử \(S\) là số chính phương thì ⇒ S là số chính phương lẻ vì \(2^{2023}-1\) là số lẻ 

Nên S có dạng \(\left(2k+1\right)^2=4k^2+4k+1=4k\left(k+1\right)+1\) khi đó \(4k\left(k+1\right)\) ⋮ 8 ⇒ S chia 8 dư 1 

Mà: \(2^{2023}-1\) chia 8 dư 7 

⇒ Mâu thuẫn   

⇒ S không phải là 1 số chính phương 

M là trung điểm của đoạn thẳng AB.

hehe=))

M là trung điểm của đoạn thẳng AB.

hehe=))

Từ 4n+5/2n-1 suy ra

4n+5:2n-1

2(2n-1)+7:2n-1

Vì 2n-1chia hết cho 2n-1

Suy ra 2(2n-1) thuộc ước của 7

Bạn tìm ước rồi lập bảng nốt nhé!

                                               GIẢI:

Ta có: 1/2=100/200=1/200+1/200+...+1/200(có 100 phân số 1/200)

Mà 1/200=1/200

      1/199>1/200

      .....

      1/101>1/200

Suy ra: 1/101+1/102+...+1/200>1/200+1/200+...+1/200(có 100 phân số 1/200)

Hay 1/2<A    ₍₁₎      

Ta có: 1=100/100=1/100+1/100+...+1/100(có 100 phân số 1/100)

MÀ     1/100>1/101

          1/100>1/102

          1/100>1/103

          ......

          1/100>1/200

Suy ra: 1/101+1/102+...+1/200<1/100+1/100+...+1/100(có 100 phân số 1/100)

Hay A<1  (2)

Từ ₍₁₎ và ₍₂₎ Ta có:

1/2<A<1

vậy1/2<A<1

Ko biết làm nhoa

Ggtyy