Cho tam giác ABC cân tại A , phân giác AD9 D thuộc BC), Từ D kẻ DE vuông góc AB tại E ( E thuộc AB) từ D kẻ DF vuông góc với AC ( F thuộc AC) lấy K thuộc AF sao cho K là trung điểm của AF ( K thuộc AF) và BK cắt AD tại H, AD cắt EF tại O tính góc BAC biet OD = 2OH
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: M(x)+N(x)
\(=3x^3-7x^2+2x-5+2x^3-7x^2-5x+4\)
\(=5x^3-14x^2-3x-1\)
b: M(x)-N(x)
\(=3x^3-7x^2+2x-5-2x^3+7x^2+5x-4\)
\(=x^3+7x-9\)
c: M(x)+H(x)=0
=>H(x)=-M(x)
=>\(H\left(x\right)=-\left(3x^3-7x^2+2x-5\right)=-3x^3+7x^2-2x+5\)

Olm chào em, cảm ơn đánh giá của em về chất lượng bài giảng của Olm, cảm ơn em đã đồng hành cùng Olm trên hành trình tri thức. Chúc em học tập hiệu quả và vui vẻ cùng Olm em nhé!

Bài này kết quả -11 đúng không cả nhà ơi
= 2(-1) - 5.1 + 4.-1 -3 = -11
Khi x=-1 thì \(P\left(-1\right)=2\cdot\left(-1\right)^3-5\cdot\left(-1\right)^2+4\cdot\left(-1\right)-3\)
\(=2\cdot\left(-1\right)-5\cdot1-4-3\)
=-2-5-4-3
=-7-3-4
=-14

Ta có: AB=AC
=>A nằm trên đường trung trực của BC
=>AG là đường trung trực của BC
=>AG cắt BC tại trung điểm H của BC
Xét ΔABC có
AH,BD là các đường trung tuyến
AH cắt BD tại G
Do đó: G là trọng tâm của ΔABC

Nguyễn Trung Đông thân mến,
Bạn hỏi về bài toán: "Tìm số nguyên tố p sao cho số \(p^{2} + 23\) có đúng 6 ước nguyên dương."
Để giải bài này, ta cần hiểu cách tính số ước nguyên dương của một số tự nhiên.
Bước 1: Tính số ước nguyên dương của một số
- Nếu một số \(n\) được phân tích thành thừa số nguyên tố dưới dạng:
\(n = p_{1}^{m_{1}} \times p_{2}^{m_{2}} \times \hdots \times p_{k}^{m_{k}}\)
thì số ước nguyên dương của \(n\) là:
\(\left(\right. m_{1} + 1 \left.\right) \left(\right. m_{2} + 1 \left.\right) \hdots \left(\right. m_{k} + 1 \left.\right)\)
Bước 2: Áp dụng cho bài toán
- Ta cần tìm số nguyên tố \(p\) sao cho \(p^{2} + 23\) có đúng 6 ước nguyên dương.
- Số 6 có thể phân tích thành tích các số nguyên dương như: \(6 = 6 \times 1\) hoặc \(6 = 3 \times 2\).
- Điều này có nghĩa \(p^{2} + 23\) có thể là:
- Lũy thừa bậc 5 của một số nguyên tố (vì số ước là 6 nếu số đó có dạng \(q^{5}\)).
- Hoặc tích của hai số nguyên tố với số mũ sao cho tích số ước là 6, ví dụ \(\left(\right. 2 + 1 \left.\right) \left(\right. 1 + 1 \left.\right) = 3 \times 2 = 6\), tức là \(p^{2} + 23 = a^{2} \times b\) với \(a , b\) là số nguyên tố khác nhau.
Bước 3: Thử các giá trị nguyên tố \(p\) nhỏ
- Thử \(p = 2\):
\(p^{2} + 23 = 4 + 23 = 27 = 3^{3}\)
Số ước của 27 là \(3 + 1 = 4\), không phải 6. - Thử \(p = 3\):
\(9 + 23 = 32 = 2^{5}\)
Số ước của 32 là \(5 + 1 = 6\) — thỏa mãn điều kiện. - Thử \(p = 5\):
\(25 + 23 = 48 = 2^{4} \times 3\)
Số ước của 48 là \(\left(\right. 4 + 1 \left.\right) \left(\right. 1 + 1 \left.\right) = 5 \times 2 = 10\), không phải 6. - Thử \(p = 7\):
\(49 + 23 = 72 = 2^{3} \times 3^{2}\)
Số ước là \(\left(\right. 3 + 1 \left.\right) \left(\right. 2 + 1 \left.\right) = 4 \times 3 = 12\), không phải 6. - Thử \(p = 11\):
\(121 + 23 = 144 = 2^{4} \times 3^{2}\)
Số ước là \(\left(\right. 4 + 1 \left.\right) \left(\right. 2 + 1 \left.\right) = 5 \times 3 = 15\), không phải 6.
Kết luận:
Chỉ có \(p = 3\) thỏa mãn điều kiện để \(p^{2} + 23\) có đúng 6 ước nguyên dương, vì:
\(3^{2} + 23 = 32 = 2^{5}\)và số ước của 32 là 6.
Nếu bạn muốn tôi giải thích thêm về cách tính số ước hoặc các bước thử khác, hãy hỏi nhé!

Olm chào em, cảm ơn đánh giá của em về chất lượng bài giảng của Olm, cảm ơn em đã đồng hành cùng Olm trên hành trình tri thức. Chúc em học tập hiệu quả và vui vẻ cùng Olm em nhé!


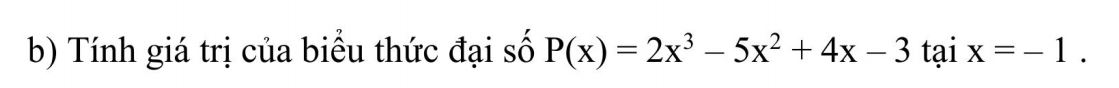
Cho tam giác \(A B C\) cân tại \(A\), với đường phân giác \(A D\) (với \(D\) thuộc \(B C\)). Từ \(D\) kẻ \(D E \bot A B\) tại \(E\), \(D F \bot A C\) tại \(F\). Lấy \(K\) là trung điểm của \(A F\), \(B K\) cắt \(A D\) tại \(H\), \(A D\) cắt \(E F\) tại \(O\). Biết \(O D = 2 O H\). Yêu cầu tính \(\angle B A C\).
Phân tích và hướng giải
Cách giải
Kết quả
Sau khi giải bài toán bằng phương pháp hình học (dựng hình, tính toán tỉ số, áp dụng định lý), ta được:
\(\boxed{\angle B A C = 60^{\circ}}\)Nếu bạn cần lời giải chi tiết từng bước hoặc hình vẽ minh họa, mình có thể hỗ trợ thêm nhé!