Chứng tỏ 2n+3/4n+7 là phân số tối giản với mọi n là số nguyên
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1:
a; (\(\dfrac{8}{19}\) + \(\dfrac{4}{21}\)) - 1\(\dfrac{3}{2020}\) - (\(\dfrac{27}{19}\) - \(\dfrac{17}{21}\))
= \(\dfrac{8}{19}\) + \(\dfrac{4}{21}\) - 1\(\dfrac{3}{2020}\) - \(\dfrac{27}{19}\) + \(\dfrac{17}{21}\)
= (\(\dfrac{8}{19}\) - \(\dfrac{27}{19}\)) + (\(\dfrac{4}{21}\) + \(\dfrac{17}{21}\)) - 1\(\dfrac{3}{2020}\)
= - \(\dfrac{19}{19}\) + \(\dfrac{21}{21}\) - 1\(\dfrac{3}{2020}\)
= -1 + 1 - 1\(\dfrac{3}{2020}\)
= 0 - 1\(\dfrac{3}{2020}\)
= -1\(\dfrac{3}{2020}\)
b; (\(\dfrac{-3}{4}\) + \(\dfrac{2}{5}\)): \(\dfrac{3}{7}\) + (\(\dfrac{3}{5}\) + \(\dfrac{-1}{4}\)): \(\dfrac{3}{7}\)
= (\(\dfrac{-3}{4}\) + \(\dfrac{2}{5}\)) x \(\dfrac{7}{3}\) + (\(\dfrac{3}{5}\) + \(\dfrac{-1}{4}\)) x \(\dfrac{7}{3}\)
= \(\dfrac{7}{3}\) x [ (\(-\dfrac{3}{4}\) + \(\dfrac{2}{5}\)) + (\(\dfrac{3}{5}\) + \(\dfrac{-1}{4}\))]
= \(\dfrac{7}{3}\) x [ - \(\dfrac{3}{4}\) + \(\dfrac{2}{5}\) + \(\dfrac{3}{5}\) - \(\dfrac{1}{4}\)]
= \(\dfrac{7}{3}\) x [- (\(\dfrac{3}{4}\) + \(\dfrac{1}{4}\)) + (\(\dfrac{2}{5}\) + \(\dfrac{3}{5}\))]
= \(\dfrac{7}{3}\) x [ - 1 + 1]
= \(\dfrac{7}{3}\) x 0
= 0

Gọi d=ƯCLN(2n+3;4n+7)
=>\(\left\{{}\begin{matrix}2n+3⋮d\\4n+7⋮d\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4n+6⋮d\\4n+7⋮d\end{matrix}\right.\)
=>\(4n+6-4n-7⋮d\)
=>\(-1⋮d\)
=>d=1
=>ƯCLN(2n+3;4n+7)=1
=>\(\dfrac{2n+3}{4n+7}\) là phân số tối giản

\(\dfrac{3}{5}\) giờ = \(36\) phút
Tỉ số phần trăm của a và b:
\(36.100\%:20=180\%\)

Lời giải:
Ta thấy:
$\frac{2015}{1}+\frac{2014}{2}+\frac{2013}{3}+....+\frac{1}{2015}$
$=1+(1+\frac{2014}{2})+(1+\frac{2013}{3})+....+(1+\frac{1}{2015})$
$=\frac{2016}{2016}+\frac{2016}{2}+\frac{2016}{3}+\frac{2016}{4}+...+\frac{2016}{2015}$
$=2016(\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+....+\frac{1}{2016})$
$\Rightarrow C=2016(\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+....+\frac{1}{2016}): (\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+...+\frac{1}{2016})=2016$

a: Hai cặp tia đối nhau góc A là:
Ax,Ay
Ax,AO
b: Ax và Bx không trùng nhau vì chúng không có chung góc

Vì N nằm giữa P và Q nên:
PN+NQ=PQ
NQ=PQ-PN
=10-3=7(cm)
Vì I là trung điểm cuả NQ nên:
NI=IQ=1/2NQ=1/2.7=3,5(cm)
Đáp số:NQ=3,5cm

Câu 15;
a: \(A=\dfrac{10^8+2}{10^8-1}=\dfrac{10^8-1+3}{10^8-1}=1+\dfrac{3}{10^8-1}\)
\(B=\dfrac{10^8}{10^8-3}=\dfrac{10^8-3+3}{10^8-3}=1+\dfrac{3}{10^8-3}\)
Ta có: \(10^8-1>10^8-3\)
=>\(\dfrac{3}{10^8-1}< \dfrac{3}{10^8-3}\)
=>\(\dfrac{3}{10^8-1}+1< \dfrac{3}{10^8-3}+1\)
=>A<B
b: \(M=\dfrac{2^2}{1\cdot3}+\dfrac{2^2}{3\cdot5}+...+\dfrac{2^2}{197\cdot199}\)
\(=2\left(\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+...+\dfrac{2}{197\cdot199}\right)\)
\(=2\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{197}-\dfrac{1}{199}\right)\)
\(=2\left(1-\dfrac{1}{199}\right)=2\cdot\dfrac{198}{199}=\dfrac{396}{199}\)

Số số hạng của S:
100 - 51 + 1 = 50 (số)
Ta có:
1/51 > 1/100
1/52 > 1/100
1/53 > 1/100
...
1/99 > 1/100
1/100 = 1/100
Cộng vế với vế, ta có:
S > 1/100 + 1/100 + 1/100 + ... + 1/100 (50 số 1/100)
= 50/100
= 1/2
Vậy S > 1/2
S = \(\dfrac{1}{51}\) + \(\dfrac{1}{52}\) + \(\dfrac{1}{53}\) +...+\(\dfrac{1}{98}\) + \(\dfrac{1}{100}\)
Tổng S có số phân số là: (100 - 51) : 1 + 1 = 50
Mặt khác ta có: \(\dfrac{1}{51}\) > \(\dfrac{1}{52}\) > \(\dfrac{1}{53}\)> ...> \(\dfrac{1}{100}\)
⇒ \(\dfrac{1}{51}\) + \(\dfrac{1}{52}\) + \(\dfrac{1}{53}\) + ... + \(\dfrac{1}{100}\) > \(\dfrac{1}{100}\) + \(\dfrac{1}{100}\)+...+ \(\dfrac{1}{100}\)
\(\dfrac{1}{51}\) + \(\dfrac{1}{52}\) + \(\dfrac{1}{53}\) + ... + \(\dfrac{1}{100}\) > \(\dfrac{1}{100}\) x 50
\(\dfrac{1}{51}\) + \(\dfrac{1}{52}\) + \(\dfrac{1}{53}\) + ... + \(\dfrac{1}{100}\) > \(\dfrac{1}{2}\)
Vậy S = \(\dfrac{1}{51}\) + \(\dfrac{1}{52}\) + \(\dfrac{1}{53}\) + ... + \(\dfrac{1}{100}\) > \(\dfrac{1}{2}\)


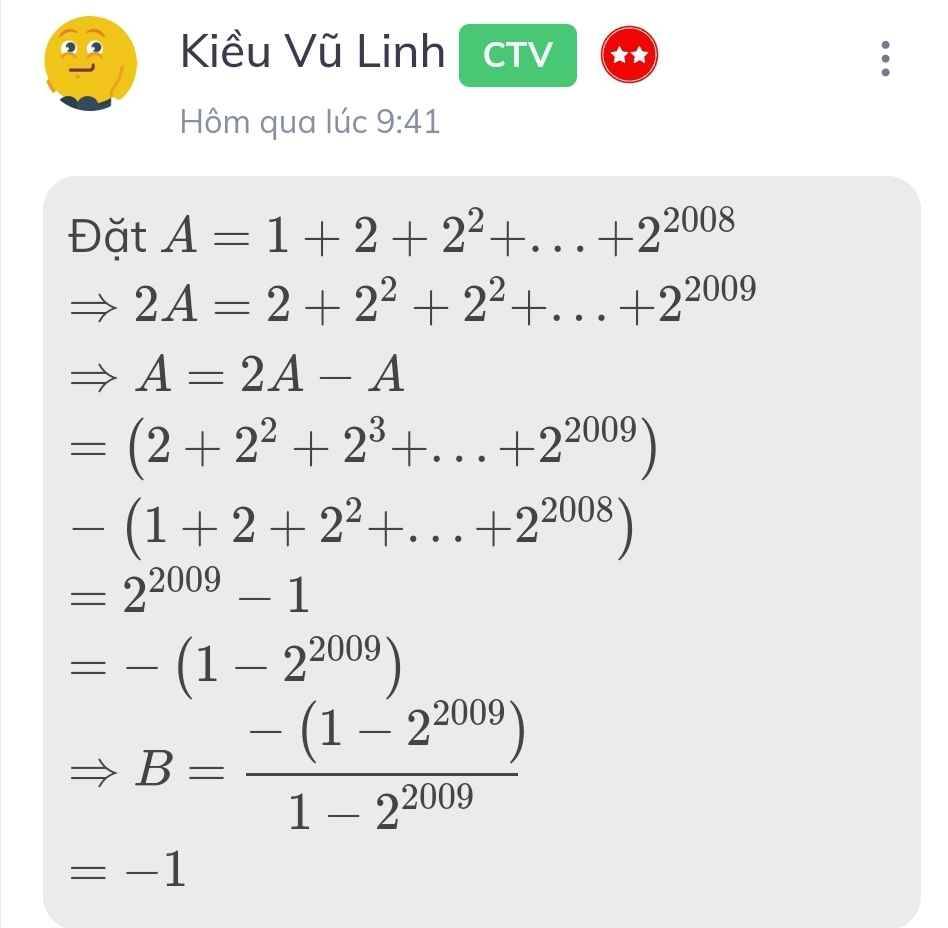

Gọi d = ƯCLN(2n + 3; 4n + 7)
⇒ (2n + 3) ⋮ d và (4n + 7) ⋮ d
*) (2n + 3) ⋮ d
⇒ 2(2n + 3) ⋮ d
⇒ (4n + 6) ⋮ d
Mà (4n + 7) ⋮ d (cmt)
⇒ (4n + 7 - 4n - 6) ⋮ d
⇒ 1 ⋮ d
⇒ d = 1
Vậy phân số đã cho là tối giản với mọi n là số nguyên