A)23/42-10/21

B)16/25-3/15

C)7/8-1/3-1/2

D)15/7-4/9-10/9

Vì \(b^2=ac\) ta suy ra \(\dfrac{a}{b}=\dfrac{b}{c}\). Đặt \(a=kb\) và \(b=kc\).

Khi đó \(\dfrac{a}{c}=\dfrac{k\left(kc\right)}{c}=k^2\). (1)

Từ tính chất của dãy tỉ số bằng nhau ta có:

\(\dfrac{a}{b}=\dfrac{b}{c}=\dfrac{2012b}{2012c}=\dfrac{a+2012b}{b+2012c}=k\), suy ra \(k^2=\dfrac{\left(a+2012b\right)^2}{\left(b+2012c\right)^2}\). (2)

Từ (1) và (2) suy ra \(k^2=\dfrac{a}{c}=\dfrac{\left(a+2012b\right)^2}{\left(b+2012c\right)^2}\) (đpcm)

Ta dựng đường thẳng CD qua song song với AB, ta có:

          \(\widehat{ACD}\) = \(\widehat{A}\) = 40⁰ (so le trong)

         \(\widehat{DCE}\)  + \(\widehat{ACD}\)  = \(\widehat{ACE}\) 

 ⇒ \(\widehat{DCE}\) = \(\widehat{ACE}\) - \(\widehat{ACD}\) = 100⁰ - 40⁰  = 60⁰

CD // AB ⇒ CD // EG 

 ⇒ \(\widehat{GEx}\) = \(\widehat{DCE}\) (hai góc đồng vị)

⇒  \(\widehat{GEx}\) = 60⁰ (vì hai góc đồng vị)

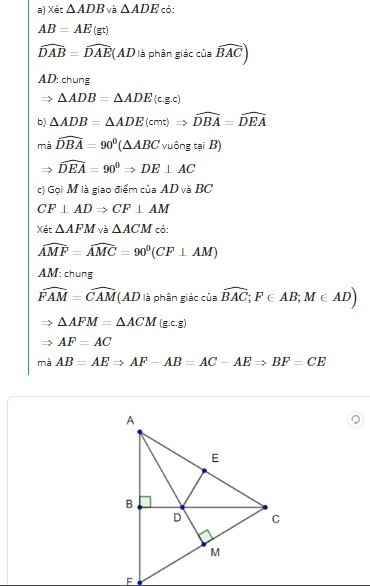
Xét \(\Delta ABC\) và \(\Delta ADE\) có:

\(AB=AD\left(gt\right)\)

\(\widehat{BAC}=\widehat{DAE}\) ( tính chất 2 góc đối đỉnh )

\(AC=AE\left(gt\right)\)

Vậy \(\Delta ABC=\) \(\Delta ADE\left(c.g.c\right)\)

\(\Rightarrow\widehat{C}=\widehat{E}\) ( 2 góc tương ứng )

Xét \(\Delta MAC\) và \(\Delta NAE\) có:

\(AC=AE\left(gt\right)\)

\(\widehat{C}=\widehat{E}\left(cmt\right)\)

\(CM=EN\left(gt\right)\)

Vậy \(\Delta MAC=\Delta NAE\left(c.g.c\right)\)

\(\Rightarrow\widehat{MAC}=\widehat{MAE}\) ( 2 góc tương ứng )

Ta có: \(\widehat{MAC}+\widehat{CAD}+\widehat{DAN}=\widehat{NAE}+\widehat{DAN}+\widehat{CAD}\)

\(\Rightarrow\widehat{MAN}=\widehat{CAE}\)

\(\Rightarrow\) 3 điểm \(M,A,N\) thẳng hàng.

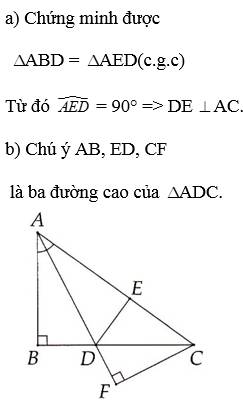
Xét △ABC và △ADE ta có:⎧⎪⎨⎪⎩AB = AD (gt)∠BAC = ∠EAD (đđ)AC = AE (gt)⇒△ABC = △AED (c.g.c) {AB = AD (gt)∠BAC = ∠EAD (đđ)AC = AE (gt)⇒△ABC = △AED (c.g.c) 

⇒ ∠ABC = ∠AED (2 góc tương ứng)

Xét △ACM và △AEN ta có:

⎧⎪⎨⎪⎩CM = EN (gt)∠ACM = ∠AEN (cmt)AC = AE (gt)⇒△ACM = △AEN (c.g.c) {CM = EN (gt)∠ACM = ∠AEN (cmt)AC = AE (gt)⇒△ACM = △AEN (c.g.c) 

⇒ ∠CAM = ∠EAN (2 góc tương ứng)

Mà ∠CAM + ∠CAN = 180^o

⇒ ∠EAN + ∠CAN = 180^o

⇒ ∠MAN = 180^o

⇒ Ba điểm M, A, N thẳng hàng (đcpm).

\(3+2^{x-1}=24-\left[4^2-\left(2^2-1\right)\right]\)

\(=3+2^{x-1}=24-\left[4^2-\left(4-1\right)\right]\)

\(=3+2^{x-1}=24-\left[16-3\right]\)

\(\Rightarrow3+2^{x-1}=11\)

\(\Rightarrow2^{x-1}=11-3\)

\(\Rightarrow2^{x-1}=8\)

\(\Rightarrow2^{x-1}=2^3\)

\(\Rightarrow x-1=3\)

\(\Rightarrow x=4\)

Vậy \(x=4\)

\(\left(x-6\right)^2=\left(x-6\right)^3\)

\(\Leftrightarrow\left(x-6\right)^2-\left(x-6\right)^3=0\)

\(\Leftrightarrow\left(x-6\right)^2.\left(1-x+6\right)\text{=}0\)

\(\Leftrightarrow\left(x-6\right)^2.\left(7-x\right)\text{=}0\)

\(\Leftrightarrow\left[{}\begin{matrix}\left(x-6\right)^2\text{=}0\\7-x\text{=}0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x\text{=}6\\x\text{=}7\end{matrix}\right.\)

Vậy.......

Để xác định xem khoảng cách trên bản vẽ có phù hợp với yêu cầu của kiến trúc sư hay không, chúng ta cần chuyển đổi đơn vị và tính toán khoảng cách thực tế giữa ổ cắm điện và vòi nước.

Theo tỉ lệ 1:20, mỗi đơn vị trên bản vẽ tương đương với 20 đơn vị trong thực tế. Do đó, để chuyển đổi từ cm sang đơn vị thực tế, ta nhân khoảng cách trên bản vẽ (2,5 cm) với tỉ lệ 20:

Khoảng cách thực tế = 2,5 cm \(\times\) 20 = 50 cm.

Khi chuyển đổi, ta thấy khoảng cách thực tế là 50 cm, nhỏ hơn yêu cầu tối thiểu của kiến trúc sư là 60 cm. Do đó, khoảng cách trên bản vẽ không phù hợp với yêu cầu của kiến trúc sư.

Lý do là vì khoảng cách được đo trên bản vẽ chỉ là khoảng cách theo tỉ lệ, và khi chuyển đổi thành khoảng cách thực tế, nó không đạt được yêu cầu tối thiểu của 60 cm. Cần điều chỉnh vị trí của ổ cắm điện và vòi nước trên bản vẽ để đảm bảo khoảng cách thực tế phù hợp với yêu cầu.

Theo bản vẽ, khoảng cách thực tế giữa ổ cắm và vòi nước của nhà chú Năm là:

2,5:(1:20)=52:120=52.20=502,5:1:20=52:120=52 . 20=50 (cm) .

Theo yêu cầu của kiến trúc sư, khoảng cách tối thiểu giữa ổ cắm và vòi nước của nhà chú Năm là 60 cm (tức là khoảng cách từ ổ cắm và vòi nước lớn hơn hoặc bằng 60 cm)

Theo bản vẽ, khoảng cách thực tế giữa ổ cắm và vòi nước của nhà chú Năm là:

\(2,5:\left(1:20\right)=\dfrac{5}{2}:\dfrac{1}{20}=50\left(cm\right)\)

Vì \(50< 60\) nên khoảng cách thực tế không phù hợp với yêu cầu của kiến trúc sư.

Nên mở ô khác nhé! Vì xác suất trúng chiếc ô tô giờ đây đến tận 2/3.

Quan sát các số trong dãy, chúng ta thấy rằng để tạo ra một số trong dãy, ta có thể nhân số trước đó với một số và cộng một số khác. Cụ thể:

Để tạo ra số 2 từ số 1, ta nhân số trước đó (1) với 2 và cộng 1:

1 \(\times\) 2 + 1 = 3.
Để tạo ra số 5 từ số 2, ta nhân số trước đó (2) với 2 và cộng 1:

2 \(\times\) 2 + 1 = 5.
Để tạo ra số 15 từ số 5, ta nhân số trước đó (5) với 3 và cộng 0:

5 \(\times\) 3 + 0 = 15.
Để tạo ra số 28 từ số 15, ta nhân số trước đó (15) với 2 và cộng 1: 15 \(\times\) 2 + 1 = 31.
Để tạo ra số 48 từ số 28, ta nhân số trước đó (28) với 2 và cộng 0: 28 \(\times\) 2 + 0 = 56.
Dựa vào quy luật này, để tìm số hạng tiếp theo của dãy, ta nhân số trước đó với một số và cộng một số khác. Áp dụng lên số cuối cùng trong dãy (48), ta có:

Số hạng tiếp theo = 48 \(\times\) 2 + 0 = 96.

Vậy, số hạng tiếp theo của dãy là 96.

\(\dfrac{11}{33}=\dfrac{11}{3.11}=\dfrac{1}{3}\)

\(\dfrac{25}{76}< \dfrac{25}{75}=\dfrac{1}{3}\)

\(\Rightarrow\dfrac{11}{33}>\dfrac{25}{76}\)

\(\Rightarrow-\dfrac{11}{33}< -\dfrac{25}{76}\)

\(\Rightarrow\dfrac{-11}{33}< \dfrac{25}{-76}\)