`@` `\text {Ans}`

`\downarrow`

`a)`

`-(-18 + 45) - (18 + 55)`

`= 18 - 45 - 18 - 55`

`= (18 - 18) - (45 + 55)`

`= -100`

`b)`

`24. (5 - 178) + 178 . (10 + 24)`

`= 24.5 - 24.178 + 178. 10 + 178. 24`

`= 24.5 + 178.(-24 + 10 + 24)`

`= 24.5 + 178.10`

`=120 + 1780`

`=``1900`

`c)`

`29.(-101)`

`= -2929`

`d)`

\((- 56 + 130) – (43 – 56) – (- 20 – 43)\)

`= -56 + 130 - 43 + 56 + 20 + 43`

`= (56 - 56) + (130 + 20) + (-43+43)`

`= 150`

6 giờ 12 phút x 2 - 10 giờ 50 phút 

= 12 giờ 24 phút - 10 giờ 50 phút 

= 1 giờ 34 phút

6 giờ 12 phút× 2 - 10 giờ 50 phút

= 12 giờ 24 phút - 10 giờ 50 phút

= 11 giờ 84 phút - 10 giờ 50 phút 

= 1 giờ 34 phút

Tỉ số phần trăm của 120 và 345 là:

         120 : 345 ≈ 0,3478

       0,3478 =  34,78%

b, Tỉ số phần trăm của 45 và 568 là:

          45 : 568 ≈ 0,0792

          0,0792 = 7,92%

Tỉ số phần trâm của 120 và 345 là:

         120 : 345 ≈ 0,3478

       0,3478 =  3478%b, Tỉ số phần trăm của 45 và 568 là:

          45 : 568 ≈ 0,0792

          0,0792 = 7,92%

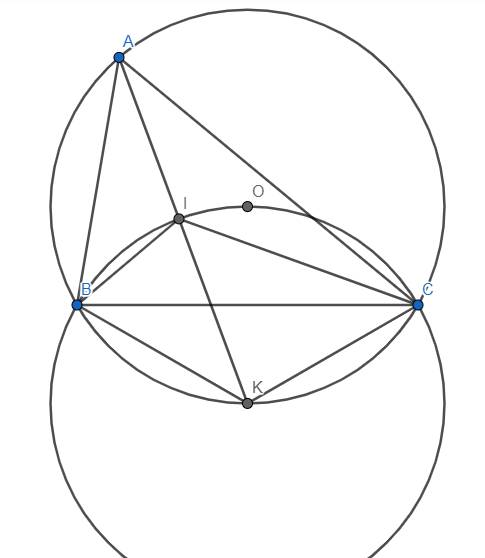
 Gọi (O) là đường tròn ngoại tiếp tam giác ABC, AI cắt (O) tại K. Theo bổ đề quen thuộc thì K là tâm của (BIC). Hơn nữa \(\widehat{BIC}=90^o+\dfrac{\widehat{BAC}}{2}=120^o\) và \(\widehat{BOC}=2\widehat{BAC}=120^o\) nên \(\widehat{BIC}=\widehat{BOC}\), suy ra tứ giác BIOC nội tiếp, suy ra \(O\in\left(K\right)\). Điều này có nghĩa bán kính của \(\left(K\right)\) chính là \(OK=2\).

Lời giải:
$\frac{6n-1}{3n-2}=\frac{2(3n-2)+3}{3n-2}$

$=2+\frac{3}{3n-2}$

Để phân số trên có giá trị nhỏ nhất thì $\frac{3}{3n-2}$ nhỏ nhất

$\Rightarrow 3n-2$ là số âm lớn nhất.

Với $n$ nguyên thì $3n-2$ âm lớn nhất bằng -2$ khi $n=0$

Khi thêm vào tử số đồng thời bớt ở mẫu số của một số tự nhiên thì 

tổng của tử số và mẫu số không thay đổi

 Tổng của tử số và mẫu số là :

         3 + 17 = 20

Ta có sơ đồ 

​  

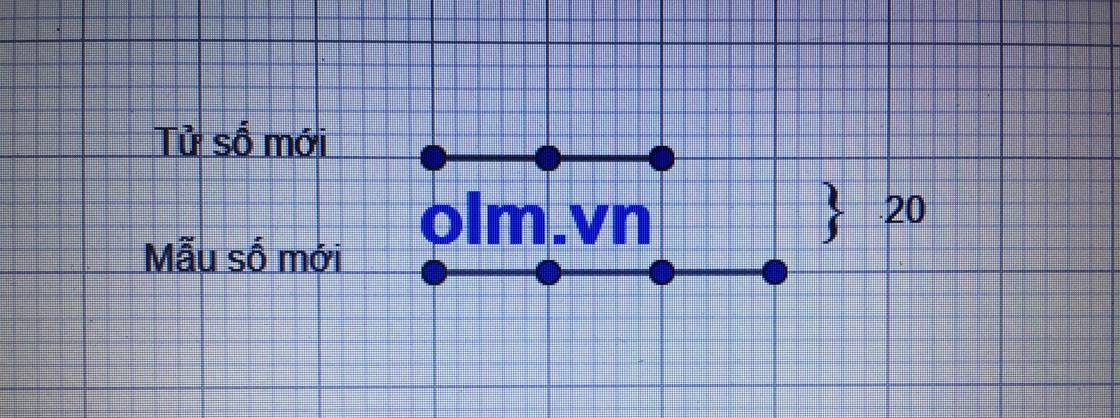
Theo sơ đồ, tử số mới là :

         20 : (2 + 3) x 2 = 8

Mẫu số mới là : 

        20 - 8 = 12

Số tự nhiên cần thêm ở tử và bớt ở mẫu là :

        8 - 3 = 5

            Đáp số :...

Khi thêm tử trừ mẫu cùng 1 số tự nhiên m, ta được phân số mới là \(\dfrac{3+m}{17-m}\) với \(m\ne17\)

Theo đề bài, ta có: 

\(\dfrac{3+m}{17-m}=\dfrac{2}{3}\\ \Leftrightarrow3m+9=34-2m\\ \Leftrightarrow5m=25\\ \Leftrightarrow m=5\left(tm\right)\)

Vậy số cần tìm là 5.

Lời giải:
Theo bài ra ta có:

$3x=2y; 4y=5z$
$\Rightarrow \frac{x}{2}=\frac{y}{3}; \frac{y}{5}=\frac{z}{4}$

$\Rightarrow \frac{x}{10}=\frac{y}{15}=\frac{z}{12}$

Đặt $\frac{x}{10}=\frac{y}{15}=\frac{z}{12}=k$

$\Rightarrow x=10k; y=15k; z=12k$
Khi đó:

$3x^2-y^2+z^2=876$

$\Rightarrow 3(10k)^2-(15k)^2+(12k)^2=876$

$\Rightarrow 219k^2=876$

$\Rightarrow k^2=4$
$\Rightarrow k=\pm 2$

Nếu $k=2$ thì $x=10k=20; y=15k=30; z=12k=24$

Nếu $k=-2$ thì $x=10k=-20; y=15k=-30; z=12k=-24$

Gọi quãng đường mỗi đoạn là : x

Thời gian đi đoạn 1, đoạn 2, đoạn 3 lần lượt là : \(\dfrac{x}{54},\dfrac{x}{45},\dfrac{x}{30}\)

Theo bài ra, ta có :

              \(\dfrac{x}{54}+\dfrac{x}{45}+\dfrac{x}{30}\) = 4

x . \(\dfrac{1}{54}\) + x . \(\dfrac{1}{45}\) + x . \(\dfrac{1}{30}\) = 4

         x.(\(\dfrac{1}{54}\) + \(\dfrac{1}{45}\) + \(\dfrac{1}{30}\)) = 4

                             x. \(\dfrac{2}{27}\) = 4

                                    x = 4 : \(\dfrac{2}{27}\)

                                    x = 4 . \(\dfrac{27}{2}\)

                                    x = 54 ⇒ 3x = 54 . 3 = 162

            Vậy độ quãng đường AB là : 162 km

Gọi ba phần đó lần lượt là: \(x;y;z\) (\(x;y;z\) > 0)

Theo bài ra ta có: \(\dfrac{x}{\dfrac{1}{5}}\) = \(\dfrac{y}{\dfrac{1}{2}}\) ⇒ 5\(x\) = 2y ⇒ \(x\) = \(\dfrac{2}{5}\)y

                              \(\dfrac{y}{\dfrac{1}{3}}\) = \(\dfrac{z}{\dfrac{1}{7}}\) ⇒ 3y = 7z  ⇒ z = \(\dfrac{3}{7}\)y

⇒ \(\dfrac{2}{5}\)y+ y+ \(\dfrac{3}{7}\)y  = 640

⇒ y.( \(\dfrac{2}{5}\) + 1 + \(\dfrac{3}{7}\)) = 640

⇒y . \(\dfrac{64}{35}\) = 640

⇒ y = 640 : \(\dfrac{64}{35}\)

y = 350

\(x\) = 350  x \(\dfrac{2}{5}\) = 140

z = 350 x \(\dfrac{3}{7}\) = 150

\(4^{39}+4^{40}+4^{41}=4^{38}.\left(4+4^2+4^3\right)=4^{38}.84⋮28\left(Vì:84⋮28\right)\)

cảm ơn