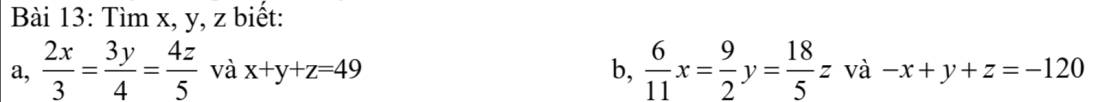 giải giúp mình với ai giải đc cảm ơn nha mình đang cần gấp
giải giúp mình với ai giải đc cảm ơn nha mình đang cần gấp
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\dfrac{3x}{8}=\dfrac{3y}{64}=\dfrac{3z}{216}\)
=>\(\dfrac{x}{8}=\dfrac{y}{64}=\dfrac{z}{216}\)
=>\(\dfrac{x}{2}=\dfrac{y}{16}=\dfrac{z}{54}\)
=>\(\dfrac{x}{1}=\dfrac{y}{8}=\dfrac{z}{27}\)
Đặt \(\dfrac{x}{1}=\dfrac{y}{8}=\dfrac{z}{27}=k\)
=>x=k; y=8k; z=27k
\(2x^2+2y^2-z^2=1\)
=>\(2k^2+2\cdot\left(8k\right)^2-\left(27k\right)^2=1\)
=>\(2k^2+128k^2-729k^2=1\)
=>\(k^2=-\dfrac{1}{599}\)(vô lý)
Vậy: KHông có bộ số (x;y;z) nào thỏa mãn yêu cầu đề bài

TH1: p=2
\(p^2+8=2^2+8=12\) không là số nguyên tố
=>Loại
TH2: p=3
\(p^2+8=3^2+8=17\) là số nguyên tố
\(p^2+2=3^2+2=11\) là số nguyên tố
=>Nhận
TH3: p=3k+1
\(p^2+8=\left(3k+1\right)^2+8=9k^2+6k+9=3\left(3k^2+2k+3\right)⋮3\)
=>p^2+8 không là số nguyên tố
=>Loại
TH4: p=3k+2
\(p^2+8=\left(3k+2\right)^2+8\)
\(=9k^2+12k+4+8=9k^2+12k+12=3\left(3k^2+4k+4\right)⋮3\)
=>p^2+8 không là số nguyên tố
=>Loại
Vậy: p=3

Để pt có nghiệm duy nhất thì: \(-\dfrac{2}{m}\ne\dfrac{1}{1}\Leftrightarrow m\ne-2\)
\(\left\{{}\begin{matrix}-2x+y=-3m-1\\mx+y=m^2+m+3\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}\left(m+2\right)y=m^2+m+3+3m+1\\-2x+y=-3m-1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{m^2+4m+4}{m+2}\\-2x+y=-3m-1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{\left(m+2\right)^2}{m+2}=m+2\\-2x+\left(m+2\right)=-3m-1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=m+2\\2x=m+2+3m+1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=m+2\\2x=4m+3\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=m+2\\x=\dfrac{4m+2}{2}\end{matrix}\right.\)
Mà: \(\left\{{}\begin{matrix}x>0\\y>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{4m+2}{3}>0\\m+2>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4m>-2\\m>-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m>-\dfrac{1}{2}\\m>-2\end{matrix}\right.\Leftrightarrow m>-\dfrac{1}{2}\)

\(2x^4+ax^3+3x^2+4x+b⋮x^2-4x+4\)
=>\(2x^4-8x^3+8x^2+\left(a+8\right)x^3-\left(4a+32\right)x^2+\left(4a+32\right)x+\left(4a+27\right)x^2-4\cdot\left(4a+27\right)x+4\cdot\left(4a+27\right)+\left(12a+80\right)x+b-16a-108⋮x^2-4x+4\)
=>\(\left\{{}\begin{matrix}12a+80=0\\b-16a-108=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}a=-\dfrac{20}{3}\\b=16a+108=\dfrac{4}{3}\end{matrix}\right.\)

Giải:
Tổng của số thứ nhất và số thứ hai là: 19 x 2 = 38
Tổng của số thứ hai và số thứ ba là: 16 x 2 = 32
Tổng của số thứ nhất và số thứ ba là: 15 x 2 = 30
Tổng của ba số là: (38 + 32 + 30) : 2 = 50
Số thứ nhất là: 50 - 32 = 18
Số thứ hai là: 38 - 18 = 20
Số thứ ba là: 30 - 18 = 12
Đáp số: Số thứ nhất là 18; số thứ hai là 20; số thứ ba là 12
Tổng của số thứ nhất và số thứ hai là: 19 x 2 = 38
Tổng của số thứ hai và số thứ ba là: 16 x 2 = 32
Tổng của số thứ nhất và số thứ ba là: 15 x 2 = 30
Tổng của ba số là: (38 + 32 + 30) : 2 = 50
Số thứ nhất là: 50 - 32 = 18
Số thứ hai là: 38 - 18 = 20
Số thứ ba là: 30 - 18 = 12
Đáp số: Số thứ nhất là 18
số thứ hai là 20
số thứ ba là 12
Tick mình nha bạn!

2 lần số viên bi của Hùng là:
15+23=38(viên)
Số viên bi của Hùng là 38:2=19(viên)

Dãy các số chẵn từ 2 đến 198 là: 2;4;6;...;196;198
SỐ số chẵn là \(\dfrac{198-2}{2}+1=\dfrac{196}{2}+1=99\left(số\right)\)
Tổng của dãy số là: \(\left(198+2\right)\cdot\dfrac{99}{2}=99\cdot100=9900\)
Trung bình cộng của dãy là:
9900:99=100
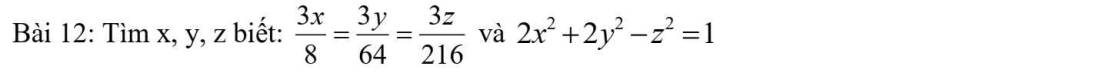

a: \(\dfrac{2x}{3}=\dfrac{3y}{4}=\dfrac{4z}{5}\)
=>\(\dfrac{x}{\dfrac{3}{2}}=\dfrac{y}{\dfrac{4}{3}}=\dfrac{z}{\dfrac{5}{4}}\)
mà x+y+z=49
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{\dfrac{3}{2}}=\dfrac{y}{\dfrac{4}{3}}=\dfrac{z}{\dfrac{5}{4}}=\dfrac{x+y+z}{\dfrac{3}{2}+\dfrac{4}{3}+\dfrac{5}{4}}=\dfrac{49}{\dfrac{49}{12}}=12\)
=>\(x=12\cdot\dfrac{3}{2}=18;y=12\cdot\dfrac{4}{3}=16;z=12\cdot\dfrac{5}{4}=15\)
b: \(\dfrac{6}{11}x=\dfrac{9}{2}y=\dfrac{18}{5}z\)
=>\(\dfrac{x}{\dfrac{11}{6}}=\dfrac{y}{\dfrac{2}{9}}=\dfrac{z}{\dfrac{5}{18}}\)
mà -x+y+z=-120
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{\dfrac{11}{6}}=\dfrac{y}{\dfrac{2}{9}}=\dfrac{z}{\dfrac{5}{18}}=\dfrac{-x+y+z}{-\dfrac{11}{6}+\dfrac{2}{9}+\dfrac{5}{18}}=\dfrac{-120}{-\dfrac{4}{3}}=90\)
=>\(x=90\cdot\dfrac{11}{6}=165;y=90\cdot\dfrac{2}{9}=20;z=90\cdot\dfrac{5}{18}=25\)
a) \(\dfrac{2x}{3}=\dfrac{3y}{4}=\dfrac{4z}{5}\Rightarrow\dfrac{x}{\dfrac{3}{2}}+\dfrac{y}{\dfrac{4}{3}}+\dfrac{z}{\dfrac{5}{4}}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{\dfrac{3}{2}}+\dfrac{y}{\dfrac{4}{3}}+\dfrac{z}{\dfrac{5}{4}}=\dfrac{x+y+z}{\dfrac{3}{2}+\dfrac{4}{3}+\dfrac{5}{4}}=\dfrac{49}{\dfrac{49}{12}}=12\)
\(\Rightarrow\dfrac{x}{\dfrac{3}{2}}=12\Rightarrow x=\dfrac{3}{2}\cdot12=18\)
\(\Rightarrow\dfrac{y}{\dfrac{4}{3}}=12\Rightarrow y=\dfrac{4}{3}\cdot12=16\)
\(\Rightarrow\dfrac{z}{\dfrac{5}{4}}=12\Rightarrow z=12\cdot\dfrac{5}{4}=15\)
Vậy: ...