10:5=2

10 : 5 = 2

A = \(\dfrac{4}{2.5}\) + \(\dfrac{4}{5.8}\)+...+ \(\dfrac{4}{47.50}\)

A = \(\dfrac{4}{3}\).( \(\dfrac{3}{2.5}+\dfrac{3}{5.8}+...+\dfrac{3}{47.50}\))

A = \(\dfrac{4}{3}\).(\(\dfrac{1}{2}\) - \(\dfrac{1}{5}\) + \(\dfrac{1}{5}\) - \(\dfrac{1}{8}\)+...+ \(\dfrac{1}{47}\) - \(\dfrac{1}{50}\))

A = \(\dfrac{4}{3}\).( \(\dfrac{1}{2}\) - \(\dfrac{1}{50}\)) 

A = \(\dfrac{4}{3}\). \(\dfrac{24}{50}\)

A = \(\dfrac{16}{25}\)

\(x_1=a>2;x_{n+1}=x_n^2-2,\forall n=1,2,...\)

mà \(n\rightarrow+\infty\)

\(\Rightarrow a\rightarrow+\infty\Rightarrow x_n\rightarrow+\infty\)

\(\Rightarrow\lim\limits_{n\rightarrow+\infty}\dfrac{1}{x_n}=0\) \(\Rightarrow\lim\limits_{n\rightarrow+\infty}\left(\dfrac{1}{x_nx_{n+1}}\right)=0\)

\(\)\(\Rightarrow\lim\limits_{n\rightarrow+\infty}\left(\dfrac{1}{x_1}+\dfrac{1}{x_1x_2}+\dfrac{1}{x_1x_2x_3}+...+\dfrac{1}{x_1x_2...x_n}\right)=0\)

...

\(...=17\left(2030+99\right)-\left(3+4\right)\)

\(=17.2129-7=36186\)

=34510+1683-7

=36186

\(\left(x+\dfrac{2}{9}\right)^2=\dfrac{4}{81}\\ \left(x+\dfrac{2}{9}\right)^2=\left(\dfrac{2}{9}\right)^2\\ x+\dfrac{2}{9}=\dfrac{2}{9}\\ x=\dfrac{2}{9}-\dfrac{2}{9}\\ x=0\)

Mình bổ sung thêm TH2 nữa. 

\(\left(x+\dfrac{2}{9}\right)^2=\left(-\dfrac{2}{9}\right)^2\\ x+\dfrac{2}{9}=-\dfrac{2}{9}\\ x=-\dfrac{2}{9}-\dfrac{2}{9}\\ x=-\dfrac{4}{9}\)

Gọi số học sinh lớp a là x (học sinh), số học sinh lớp b là y (học sinh), số học sinh lớp c là z (học sinh)

Theo đề bài, ta có: 

\(\left\{{}\begin{matrix}x=\dfrac{8}{9}y\Rightarrow y=\dfrac{9}{8}x\\z=\dfrac{17}{16}x\end{matrix}\right.\)

Có: \(x+y+z=102\\ \Rightarrow x+\dfrac{9}{8}x+\dfrac{17}{16}x=102\\ \Leftrightarrow\dfrac{51}{16}x=102\\ \Leftrightarrow x=32\\ \Rightarrow y=\dfrac{9}{8}x=36\\ \Rightarrow z=\dfrac{17}{16}x=34\)

Vậy lớp a có 32 học sinh, lớp b có 36 học sinh, lớp c có 34 học sinh.

Số phân số của lớp b so với cả 3 lớp:

\(1+\dfrac{8}{9}+\dfrac{17}{16}.\dfrac{8}{9}=\dfrac{17}{6}\)

Số  học sinh khối b :

\(102:\dfrac{17}{6}=102.\dfrac{6}{17}=36\) (học sinh)

Số học sinh khối a:

\(36.\dfrac{8}{9}=32\) (học sinh)

Số học sinh khối c:

\(102-\left(36+32\right)=34\) (học sinh)

Bài giải

a. Ta có: \(5+6=11\)

Vậy số học sinh nữ bằng số phần số học sinh toàn trường là:

\(5:11=\dfrac{5}{11}\)(số học sinh toàn trường)

Số học sinh nam bằng số phần số học sinh toàn trường là:

\(1-\dfrac{5}{11}=\dfrac{6}{11}\)(số học sinh toàn trường)

b. Ta có sơ đồ: 

Nam: |---|---|---|---|---|---|

Nữ:    |---|---|---|---|---|

Theo sơ đồ, tổng số phần bằng nhau là:

\(6+5=11\)(phần)

Số học sinh nam là:

\(1210:11\times6=660\)(học sinh)

Số học sinh nữ là:

\(1210-660=550\)(học sinh)

Đ/s: ...

\(3x-2y=8\\ \left[{}\begin{matrix}3x-2y=8\\3x-2y=8\end{matrix}\right.\\ \left[{}\begin{matrix}3x=2y+8\\2y=3x-8\end{matrix}\right.\\ \left[{}\begin{matrix}\dfrac{3x}{3}=\dfrac{2y+8}{3}\\\dfrac{2y}{2}=\dfrac{3x-8}{2}\end{matrix}\right.\\ \left[{}\begin{matrix}x=\dfrac{2y+8}{3}\\y=\dfrac{3x-8}{2}\end{matrix}\right.\)

Thêm dấu '' \(\Leftrightarrow\) '' mỗi đầu dòng hộ mình nhé.

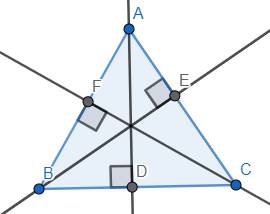
Nhận xét: AD, BE và CF là các đường cao, chúng đồng quy tại một điểm.

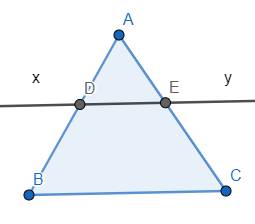
Dễ dàng thấy được \(\widehat{ABC}=\widehat{ADE}\) và \(\widehat{ACB}=\widehat{AED}\) (vì với mỗi cặp thì hai góc của cặp đó là hai góc so le trong)

Vì \(\widehat{ADE}\) và \(\widehat{BDE}\) là hai góc kề bù nên \(\widehat{ADE}+\widehat{BDE}=180^o\)

Mà \(\widehat{ABC}=\widehat{ADE}\) nên \(\widehat{ABC}+\widehat{BDE}=180^o\), suy ra \(\widehat{ABC}\) và \(\widehat{BDE}\) là hai góc bù nhau.

Suy luận tương tự như trên, ta được \(\widehat{ACB}\) và \(\widehat{CED}\) là hai góc bù nhau.

Bạn xem lại đề