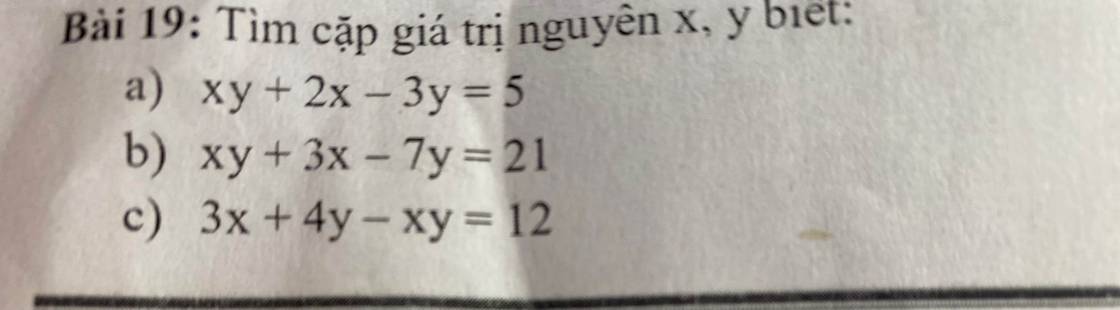 giúp mik vs ạ :
giúp mik vs ạ :
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


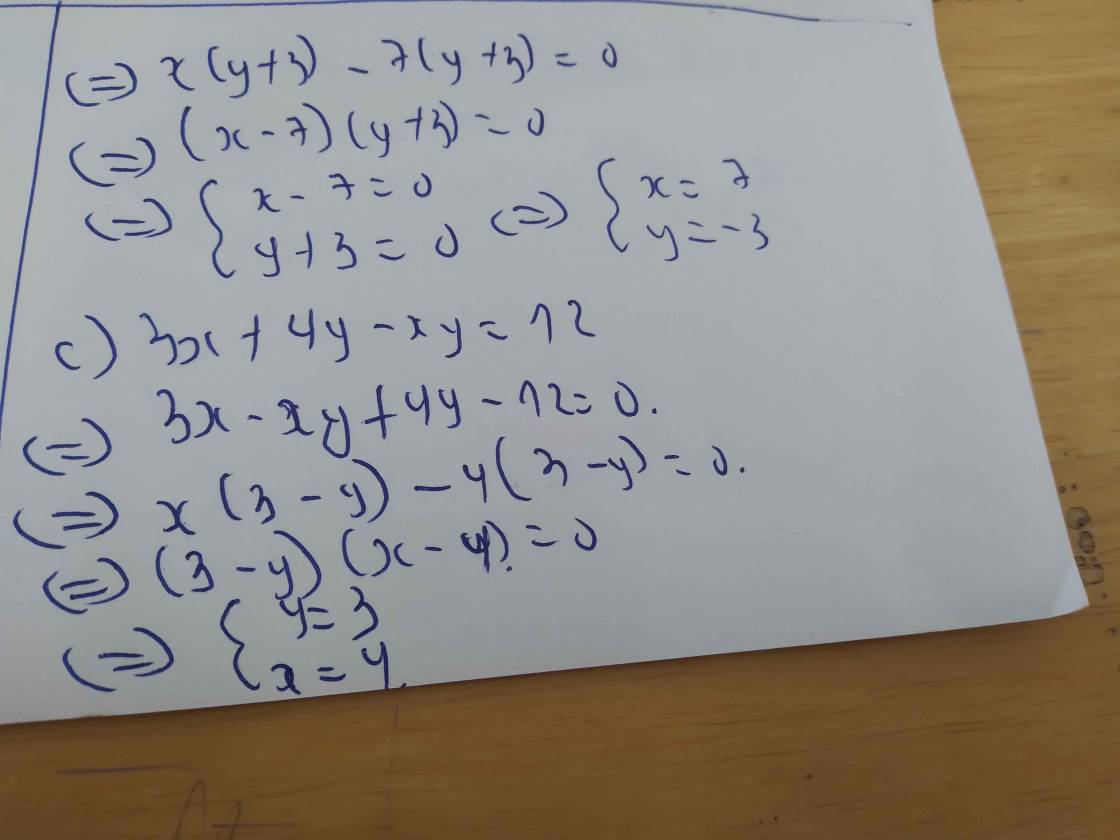

a) Đặt A = 10.11 + 11.12 + 12.13 + ... + 86.86
⇒ 3A = 10.11.3 + 11.12.3 + 12.13.3 + ... + 85.86.3
= 10.11.(12 - 9) + 11.12.(13 - 10) + 12.13.(14 - 11) + ... + 85.86.(87 - 84)
= 10.11.12 - 9.10.11 + 11.12.13 - 10.11.12 + 12.13.14 - 11.12.13 + ... + 85.86.87 - 84.85.86
= -9.10.11 + 85.86.87
= 634980
⇒ A = 634980 : 3 = 211660
b) Đặt B = 1.4 + 4.7 + 7.10 + ... + 37.40 + 40.43
⇒ 9B = 1.4.9 + 4.7.9 + 7.10.9 + ... + 37.40.9 + 40.43.9
= 1.4.(7 + 2) + 4.7.(10 - 1) + 7.10.(13 - 4) + ... + 37.40.(43 - 34) + 40.43.(46 - 37)
= 1.4.7 + 1.2.4 + 4.7.10 - 1.4.7 + 7.10.13 - 4.7.10 + ... + 37.40.43 - 34.37.40 + 40.43.46 - 37.40.43
= 1.2.4 + 40.43.46
= 8 + 79120
= 79128
⇒ B = 79128 : 9 = 8792

Gọi d=ƯCLN(2n+1;3n+2)
=>\(\left\{{}\begin{matrix}2n+1⋮d\\3n+2⋮d\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}6n+3⋮d\\6n+4⋮d\end{matrix}\right.\)
=>\(6n+4-6n-3⋮d\)
=>\(1⋮d\)
=>d=1
=>ƯCLN(2n+1;3n+2)=1
=>\(\dfrac{2n+1}{3n+2}\) là phân số tối giản

Đặt \(B=4^{2023}+4^{2022}+...+4^2+5\)
=>\(B=4^{2023}+4^{2022}+...+4^2+4+1\) và \(A=75B+25\)
\(B=4^{2023}+4^{2022}+...+4^2+4+1\)
=>\(4B=4^{2024}+4^{2023}+...+4^3+4^2+4\)
=>\(4B-B=4^{2024}+4^{2023}+...+4^3+4^2+4-4^{2023}-4^{2022}-...-4^2-4-1\)
=>\(3B=4^{2024}-1\)
=>\(B=\dfrac{4^{2024}-1}{3}\)
\(A=75\cdot B+25=75\cdot\dfrac{4^{2024}-1}{3}+25\)
\(=25\left(4^{2024}-1\right)+25\)
\(=25\cdot4^{2024}⋮4^{2024}\)

\(3\cdot5^{x-1}+6250=25^3\)
=>\(\dfrac{3}{5}\cdot5^x=25^3-6250=9375\)
=>\(5^x=9375:\dfrac{3}{5}=15625\)
=>x=6

a: Vì O nằm trên đoạn AB
nên O nằm giữa A và B
=>OA+OB=AB
=>OA+2=7
=>OA=5(cm)
b: I nằm trên đoạn AO
=>I nằm giữa A và O
=>AI+IO=AO
=>IO+3=5
=>IO=2(cm)
Vì OA và OB là hai tia đối nhau
nên OI và OB là hai tia đối nhau
=>O nằm giữa I và B
mà OI=OB(=2cm)
nên O là trung điểm của BI

Vì AP và AQ là hai tia đối nhau
nên A nằm giữa P và Q

\(A=\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+...+\dfrac{1}{98\cdot99}+\dfrac{1}{99\cdot100}\)
\(=\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{99}-\dfrac{1}{100}\)
\(=\dfrac{1}{2}-\dfrac{1}{100}=\dfrac{49}{100}\)
Hãy viết phân số 7/12 dưới dạng tổng của hai phân số có tử số là 1 mẫu số khác nhau