8⁵ = (2³)⁵ = 2¹⁵ = 2.2¹⁴

3.4⁷ = 3.(2²)⁷ = 3.2¹⁴

Do 2 < 3 nên 2.2¹⁴ < 3.2¹⁴

Vậy 8⁵ < 3.4⁷

\(8^5=2^{15}=2.2^{14}\)

\(3.4^7=3.2^{14}>2.2^{14}\)

\(\Rightarrow8^5< 3.4^7\)

a) \(\dfrac{17}{20}< \dfrac{18}{20}< \dfrac{18}{19}\Rightarrow\dfrac{17}{20}< \dfrac{18}{19}\)

b) \(\dfrac{19}{18}>\dfrac{19+2024}{18+2024}=\dfrac{2023}{2022}\Rightarrow\dfrac{19}{18}>\dfrac{2023}{2022}\)

c) \(\dfrac{135}{175}=\dfrac{27}{35}\)

\(\dfrac{13}{17}=\dfrac{26}{34}< \dfrac{26+1}{34+1}=\dfrac{27}{35}\)

\(\Rightarrow\dfrac{13}{17}< \dfrac{135}{175}\)

`# \text {Kaizu DN}`

`a)`

`(3x + 6) + (7x - 14) = 0?`

\(\Rightarrow3x+6+7x-14=0\\ \Rightarrow\left(3x+7x\right)+\left(6-14\right)=0\\ \Rightarrow10x-8=0\\ \Rightarrow10x=8\Rightarrow x=\dfrac{8}{10}\\ \Rightarrow x=\dfrac{4}{5}\)

Vậy, \(x=\dfrac{4}{5}\) 

`b)`

`17y + 35 + 4x + 17 = 42`

\(\Rightarrow\left(17y+17\right)+\left(35+4x\right)=42\\ \Rightarrow17\left(y+1\right)+\left(35+4x\right)=42\)

Bạn xem lại đề ;-;.

a) \(\dfrac{5}{3a-1}=1\)

\(\Rightarrow3a-1=5\)

\(\Rightarrow3a=6\)

\(\Rightarrow a=\dfrac{6}{3}=2\)

b) \(\dfrac{5}{3a-1}=-5\)

\(\Rightarrow3a-1=5:\left(-5\right)=-1\)

\(\Rightarrow3a=-1+1=0\)

\(\Rightarrow a=0:3=0\)

\(a,2\dfrac{1}{2}-x+\dfrac{4}{5}=\dfrac{2}{3}-\left(-\dfrac{4}{7}\right)\\ \Rightarrow\dfrac{5}{2}-x+\dfrac{4}{5}=\dfrac{26}{21}\\ \Rightarrow\dfrac{5}{2}-x=\dfrac{46}{105}\\ \Rightarrow x=\dfrac{433}{210}\\ b,-\dfrac{4}{7}-x=\dfrac{3}{5}-2x\\ \Rightarrow2x-\dfrac{4}{7}-x=\dfrac{3}{5}\\ \Rightarrow2x-x=\dfrac{41}{35}\\ \Rightarrow x=\dfrac{41}{35}\\ c,\left(\dfrac{3}{8}-\dfrac{1}{5}\right)+\left(\dfrac{5}{8}-x\right)=\dfrac{1}{5}\\ \Rightarrow\dfrac{7}{40}+\dfrac{5}{8}-x=\dfrac{1}{5}\\ \Rightarrow\dfrac{4}{5}-x=\dfrac{1}{5}\\ \Rightarrow x=\dfrac{3}{5}.\)

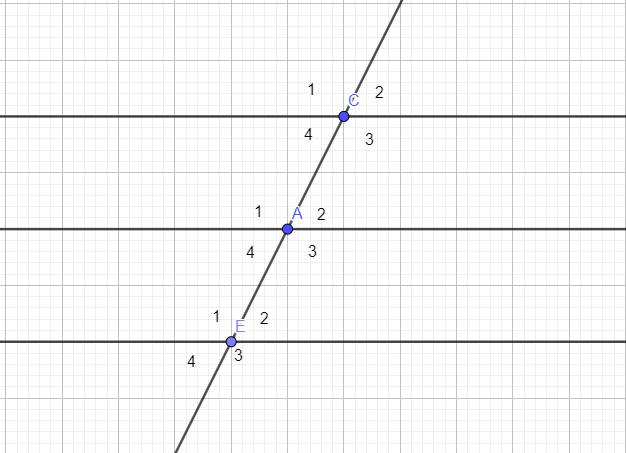
Đồng vị: \(\widehat{C_2}=\widehat{A_2};\widehat{E_2}=\widehat{A_2};\widehat{E_2}=\widehat{C_2}\)

So le trong: \(\widehat{C_4}=\widehat{A_2};\widehat{C_3}=\widehat{A_1};\widehat{A_3}=\widehat{E_1}\)

Trong cùng phía: \(\widehat{A_3}+\widehat{E_2}=180^o;\widehat{A_4}+\widehat{E_1}=180^o;\widehat{C_3}+\widehat{A_1}=180^o\) 

\(\widehat{B_1}\) = \(\widehat{B_2}\) = 100⁰ (hai góc đối đỉnh)

\(\widehat{C_2}\) = \(\widehat{B_1}\) = 100⁰ (hai góc đồng vị)

\(\widehat{C_3}\) + \(\widehat{C_2}\) = 180⁰ ⇒ \(\widehat{C_3}\) = 180⁰ - 100⁰ = 80⁰

\(\widehat{D_1}\) = \(\widehat{A_1}\) = 60⁰ (so le trong) 

\(\widehat{DAH}\) = 90⁰ - 60⁰ = 30⁰

Mik ns mấy cái số tại mik sợ nó bị mờ nhoa

a) \(-\dfrac{3}{5}-x=-0,75\)

\(\Rightarrow-\dfrac{3}{5}-x=-\dfrac{3}{4}\)

\(\Rightarrow x=\dfrac{3}{4}-\dfrac{3}{5}\)

\(\Rightarrow x=\dfrac{15}{20}-\dfrac{12}{20}=\dfrac{8}{20}=\dfrac{2}{5}\)

b) \(1\dfrac{4}{5}=-0,15-x\)

\(\Rightarrow\dfrac{9}{5}=-\dfrac{3}{20}-x\)

\(\Rightarrow x=-\dfrac{3}{20}-\dfrac{9}{5}\)

\(\Rightarrow x=-\dfrac{3}{20}-\dfrac{36}{20}=-\dfrac{39}{20}\)

c) \(x+\dfrac{1}{3}=\dfrac{2}{5}-\left(-\dfrac{1}{3}\right)\)

\(\Rightarrow x+\dfrac{1}{3}=\dfrac{2}{5}+\dfrac{1}{3}\)

\(\Rightarrow x=\dfrac{2}{5}+\dfrac{1}{3}-\dfrac{1}{3}=\dfrac{2}{5}\)

a) \(-\dfrac{3}{5}-x=-0,75\)

\(x=-\dfrac{3}{5}+0,75=\dfrac{3}{5}+\dfrac{3}{4}\)

\(x=\dfrac{27}{20}\)

________

b) \(1\dfrac{4}{5}=-0,15-x\)

\(=>-0,15-x=\dfrac{9}{5}\)

\(x=\dfrac{-3}{20}-\dfrac{9}{5}=\dfrac{-3}{20}-\dfrac{36}{20}\)

\(x=\dfrac{-39}{20}\)

c) \(x+\dfrac{1}{3}=\dfrac{2}{5}-\left(-\dfrac{1}{3}\right)=\dfrac{6}{15}+\dfrac{5}{15}\)

\(x+\dfrac{1}{3}=\dfrac{11}{15}\)

\(x=\dfrac{11}{15}-\dfrac{1}{3}=\dfrac{11}{15}-\dfrac{5}{15}\)

\(x=\dfrac{6}{15}=\dfrac{2}{5}\)

\(a,0,\left(123\right)+0,\left(876\right)=\dfrac{123}{999}+\dfrac{876}{999}=\dfrac{999}{999}=1\left(đpcm\right)\\ b,0,\left(123\right).3+0,\left(630\right)=\dfrac{123}{999}.3+\dfrac{630}{999}=\dfrac{369}{999}+\dfrac{630}{999}=\dfrac{999}{999}=1\left(đpcm\right)\)