1 năm gồm có 4 quý.viết tập hợp A gồm các tháng của quý 3 trong năm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


`a, x^2-6x+9-y^2`
`= (x-3)^2-y^2`
`=(x-3-y)(x-3+y)`
`b,x^2-4y^2+4x+4`
`= (x^2+4x+4)-(2y)^2`
`= (x+2)^2-(2y)^2`
`=(x+2-2y)(x+2+2y)`
`c, 4x^2+4x-y^2+1`
`=4x^2+4x+1-y^2`
`=(2x+1)^2-y^2`
`=(2x+1-y)(2x+1+y)`
`d, 4x^2-y^2+4y-4`
`= 4x^2-(y^2-4y+4)`
`= (2x)^2-(y-2)^2`
`= (2x-y+2)(2x+y-2)`

Ta có:
`(25/13)^15 = (25^15)/(13^15) > 1`
`(13/25)^20 = (13^20)/(25^20) < 1`
`-> (13/25)^20 < 1 < (25/13)^15`
Vậy: `(25/13)^15 > (13/25)^20`
(\(\dfrac{25}{13}\))15 > 115 > 1
(\(\dfrac{13}{25}\))20 < 120 < 1
Vậy (\(\dfrac{25}{13}\))15 > (\(\dfrac{13}{25}\))20

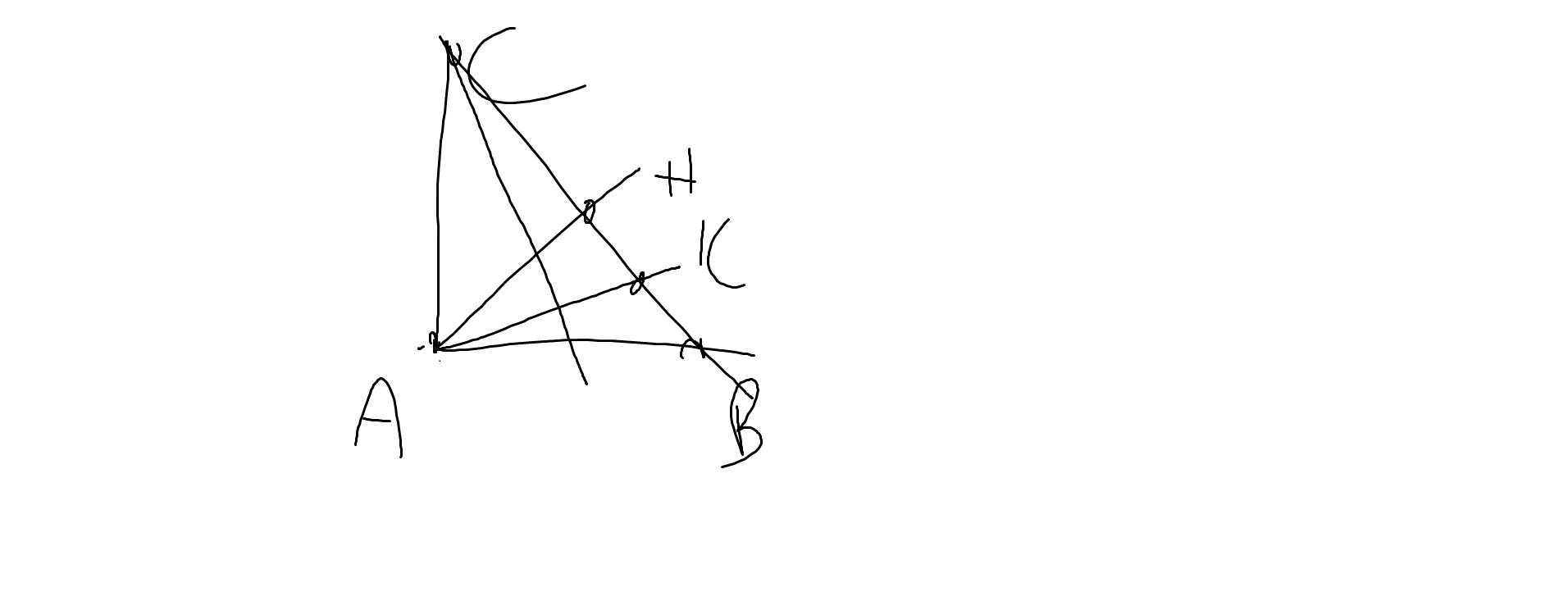
a: Ta có: \(\widehat{HAC}+\widehat{ACB}=90^0\)(ΔAHC vuông tại H)
\(\widehat{ABC}+\widehat{ACB}=90^0\)(ΔABC vuông tại A)
Do đó: \(\widehat{HAC}=\widehat{ABC}\)
b: Ta có: \(\widehat{CAK}+\widehat{BAK}=\widehat{BAC}=90^0\)
\(\widehat{CKA}+\widehat{HAK}=90^0\)(ΔHAK vuông tại H)
mà \(\widehat{BAK}=\widehat{HAK}\)(AK là phân giác của góc HAB)
nên \(\widehat{CAK}=\widehat{CKA}\)
c: Xét ΔCAK có \(\widehat{CAK}=\widehat{CKA}\)
nên ΔCAK cân tại C
ΔCAK cân tại C
mà CP là đường phân giác
nên CP\(\perp\)AK


Cách 1: Số dầu đã lấy ra ở cả hai lần là:
3,5+2,75=6,25(lít)
Số lít dầu còn lại là:
17,65-6,25=11,4(lít)
Cách 2:
Số lít dầu còn lại sau khi lấy ra lần 1 là:
17,65-3,5=14,15(lít)
Số lít dầu còn lại sau khi lấy ra lần 2 là:
14,15-2,75=11,4(lít)


ĐKXĐ: \(\left\{{}\begin{matrix}x>=0\\x\ne4\end{matrix}\right.\)
\(P=\left(\dfrac{2}{x-4}+\dfrac{1}{\sqrt{x}+2}\right):\dfrac{1}{\sqrt{x}+2}\)
\(=\dfrac{2+\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\cdot\dfrac{\sqrt{x}+2}{1}=\dfrac{\sqrt{x}}{\sqrt{x}-2}\)
Để P=3/2 thì \(\dfrac{\sqrt{x}}{\sqrt{x}-2}=\dfrac{3}{2}\)
=>\(3\left(\sqrt{x}-2\right)=2\sqrt{x}\)
=>\(3\sqrt{x}-2\sqrt{x}=6\)
=>\(\sqrt{x}=6\)
=>x=36(nhận)




A={tháng bảy, tháng tám, tháng chín}
\(A=\){tháng 7 ;tháng 8 ,tháng 9}