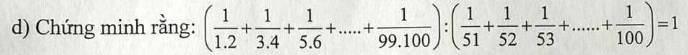
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\dfrac{2a-1}{4}-\dfrac{3a+2}{3}+2a\)
\(=\dfrac{3\left(2a-1\right)-4\left(3a+2\right)+24a}{12}\)
\(=\dfrac{6a-3-12a-8+24a}{12}=\dfrac{18a-11}{12}\)

Bài 1:
a: \(\dfrac{6}{13}\cdot\dfrac{5}{18}+\dfrac{-7}{24}+\dfrac{5}{18}\cdot\dfrac{7}{13}+\dfrac{-5}{24}\)
\(=\dfrac{5}{18}\left(\dfrac{6}{13}+\dfrac{7}{13}\right)+\left(-\dfrac{7}{24}+\dfrac{-5}{24}\right)\)
\(=\dfrac{5}{18}+\dfrac{-12}{24}=\dfrac{5}{18}-\dfrac{1}{2}=\dfrac{-4}{18}=-\dfrac{2}{9}\)
b: \(4\dfrac{1}{20}\left(-\dfrac{2}{3}\right)^2+\left(0,8-\dfrac{8}{15}\right):\dfrac{-4}{7}\)
\(=\dfrac{81}{20}\cdot\dfrac{4}{9}+\left(\dfrac{4}{5}-\dfrac{8}{15}\right)\cdot\dfrac{-7}{4}\)
\(=\dfrac{9}{5}+\dfrac{4}{15}\cdot\dfrac{-7}{4}=\dfrac{9}{5}-\dfrac{7}{15}=\dfrac{20}{15}=\dfrac{4}{3}\)
c: \(\left(3\dfrac{3}{29}-3\dfrac{1}{5}+2\dfrac{7}{11}\right)-\left(2\dfrac{3}{29}-3\dfrac{4}{11}\right)\)
\(=3+\dfrac{3}{29}-3-\dfrac{1}{5}+2+\dfrac{7}{11}-2-\dfrac{3}{29}+3+\dfrac{4}{11}\)
\(=\left(3-3+2-2+3\right)+\left(\dfrac{3}{29}-\dfrac{3}{29}\right)+\left(\dfrac{7}{11}+\dfrac{4}{11}\right)-\dfrac{1}{5}\)
\(=3+1-\dfrac{1}{5}=4-\dfrac{1}{5}=3,8\)
d: \(\dfrac{-1}{4}\cdot\dfrac{152}{11}+\dfrac{1}{4}\cdot\dfrac{-68}{11}\)
\(=\dfrac{1}{4}\left(-\dfrac{152}{11}-\dfrac{68}{11}\right)\)
\(=\dfrac{1}{4}\cdot\dfrac{-220}{11}=\dfrac{1}{4}\cdot\left(-20\right)=-5\)
Bài 2:
a: \(\dfrac{5}{6}+\left(5x+\dfrac{3}{2}\right):\dfrac{8}{15}=2\dfrac{1}{12}\)
=>\(\left(5x+\dfrac{3}{2}\right):\dfrac{8}{15}=\dfrac{25}{12}-\dfrac{5}{6}=\dfrac{25-10}{12}=\dfrac{15}{12}=\dfrac{5}{4}\)
=>\(5x+\dfrac{3}{2}=\dfrac{8}{15}\cdot\dfrac{5}{4}=\dfrac{2}{3}\)
=>\(5x=\dfrac{2}{3}-\dfrac{3}{2}=\dfrac{-5}{6}\)
=>\(x=-\dfrac{1}{6}\)
b: \(\dfrac{2}{3}\left(x+\dfrac{9}{5}\right)-\dfrac{3}{10}\left(5x-\dfrac{1}{3}\right)=\dfrac{7}{15}\)
=>\(\dfrac{2}{3}x+\dfrac{6}{5}-\dfrac{3}{2}x+\dfrac{1}{10}=\dfrac{7}{15}\)
=>\(x\left(\dfrac{2}{3}-\dfrac{3}{2}\right)=\dfrac{7}{15}-\dfrac{6}{5}-\dfrac{1}{10}=\dfrac{14-36-3}{30}=\dfrac{-25}{30}=\dfrac{-5}{6}\)
=>\(x\cdot\dfrac{-5}{6}=\dfrac{-5}{6}\)
=>x=1
c: \(\dfrac{3}{5}x-\dfrac{1}{2}=\dfrac{7}{10}\)
=>\(\dfrac{3}{5}x=\dfrac{7}{10}+\dfrac{1}{2}=\dfrac{12}{10}=\dfrac{6}{5}\)
=>x=2
d: \(\dfrac{1}{5}+\dfrac{4}{5}:x=-1\)
=>\(\dfrac{4}{5}:x=-1-\dfrac{1}{5}=\dfrac{-6}{5}\)
=>\(x=-\dfrac{4}{5}:\dfrac{6}{5}=\dfrac{-2}{3}\)
Bài 1:
a.
$=(\frac{6}{13}.\frac{5}{18}+\frac{5}{18}.\frac{7}{13})-(\frac{7}{24}+\frac{5}{24})$
$=\frac{5}{18}(\frac{6}{13}+\frac{7}{13})-\frac{12}{24}$
$=\frac{5}{18}.1-\frac{1}{2}=\frac{5}{18}-\frac{1}{2}=\frac{-2}{9}$
b.
$=\frac{81}{20}.\frac{4}{9}+\frac{4}{15}.\frac{-7}{4}$
$=\frac{9}{5}+\frac{-7}{15}=\frac{4}{3}$
c.
$=3\frac{3}{29}-3\frac{1}{5}+2\frac{7}{11}-2\frac{3}{29}+3\frac{4}{11}$
$=(3-3+2-2+3)+(\frac{3}{29}-\frac{3}{29})+(\frac{7}{11}+\frac{4}{11})$
$=3+0+\frac{11}{11}=3+1=4$
d.
$=\frac{1}{4}.\frac{-152}{11}+\frac{1}{4}.\frac{-68}{11}$
$=\frac{1}{4}(\frac{-152}{11}+\frac{-68}{11})$
$=\frac{1}{4}.(-20)=-5$

\(A=\dfrac{2n+2}{n+2}+\dfrac{5n+17}{n+2}-\dfrac{3n}{n+2}\)
\(=\dfrac{2n+2+5n+17-3n}{n+2}=\dfrac{4n+19}{n+2}\)
Để A là số nguyên thì \(4n+19⋮n+2\)
=>\(4n+8+11⋮n+2\)
=>\(11⋮n+2\)
=>\(n+2\in\left\{1;-1;11;-11\right\}\)
=>\(n\in\left\{-1;-3;9;-13\right\}\)
Lời giải:
\(A=\frac{2n+2}{n+2}+\frac{5n+17}{n+2}-\frac{3n}{n+2}=\frac{2n+2+5n+17-3n}{n+2}\\
=\frac{4n+19}{n+2}=\frac{4(n+2)+11}{n+2}=4+\frac{11}{n+2}\)
Với $n$ nguyên, để $A$ nguyên thì $11\vdots n+2$
$\Rightarrow n+2\in\left\{1; -1; 11; -11\right\}$
$\Rightarrow n\in\left\{-1; -3; 9; -13\right\}$

Lời giải:
$4\equiv 1\pmod 3$
$\Rightarrow 4^{2024}+1\equiv 1^{2024}+1\equiv 2\pmod 3$
Một scp khi chia cho 3 thì chỉ có thể có số dư là $0$ hoặc $1$
$\Rightarrow 4^{2024}+1$ không phải số chính phương.

a: Số học sinh khá là \(45\cdot40\%=18\left(bạn\right)\)
Số học sinh còn lại là 45-18=27(bạn)
Số học sinh trung bình là \(27\left(1-\dfrac{5}{9}\right)=27\cdot\dfrac{4}{9}=12\left(bạn\right)\)
b: Số học sinh nữ là \(12:\dfrac{5}{6}=12\cdot\dfrac{6}{5}=\dfrac{72}{5}=14,4\left(bạn\right)\)
=>Đề sai rồi bạn


Lời giải:
Đặt $A=x^2+x^4+....+x^{100}$
$\Rightarrow x^2A=x^4+x^6+....+x^{100}+x^{102}$
$\Rightarrow x^2A-A=x^{102}-x^2$
$\Rightarrow A(x^2-1)=x^2(x^{100}-1)$
$\Rightarrow A=\frac{x^2(x^{100}-1)}{x^2-1}$
$\Rightarrow A.\frac{x^2-1}{x^{100}-1}=\frac{x^2(x^{100}-1)}{x^2-1}.\frac{x^2-1}{x^{100}-1}=x^2$ (đpcm)

a: is studying
b: are having
c: aren't studying
d: are having
e: are making


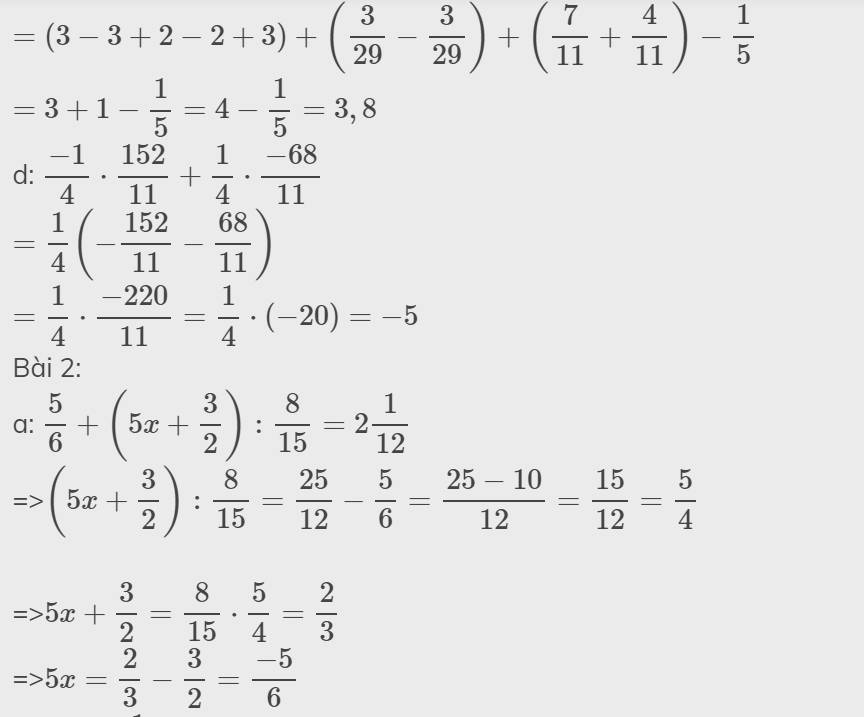



Lời giải:
$\frac{1}{1.2}+\frac{1}{3.4}+\frac{1}{5.6}+...+\frac{1}{99.100}$
$=\frac{2-1}{1.2}+\frac{4-3}{3.4}+\frac{6-5}{5.6}+...+\frac{100-99}{99.100}$
$=1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}-\frac{1}{6}+....+\frac{1}{99}-\frac{1}{100}$
$=(1+\frac{1}{3}+\frac{1}{5}+...+\frac{1}{99})-(\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+....+\frac{1}{100})$
$=(1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+...+\frac{1}{99}+\frac{1}{100})-2(\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+....+\frac{1}{100})$
$=(1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+...+\frac{1}{99}+\frac{1}{100})-(1+\frac{1}{2}+\frac{1}{3}+....+\frac{1}{50})$
$=\frac{1}{51}+\frac{1}{52}+...+\frac{1}{100}$
$\Rightarrow (\frac{1}{1.2}+\frac{1}{3.4}+\frac{1}{5.6}+...+\frac{1}{99.100}):(\frac{1}{51}+\frac{1}{52}+...+\frac{1}{100})=1$