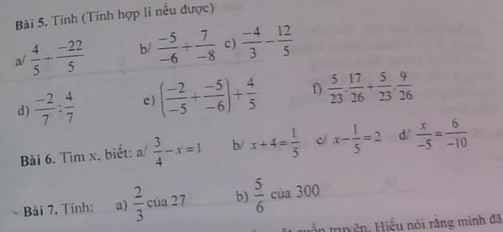
giải chi tiết
chỉ giải bài 5e,f và bài 6 ,7
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ĐKXĐ: x<>-1
Để B là số nguyên tố thì \(\left\{{}\begin{matrix}2-3x⋮x+1\\B>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-3x-3+5⋮x+1\\\dfrac{2-3x}{x+1}>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}5⋮x+1\\\dfrac{3x-2}{x+1}< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+1\in\left\{1;-1;5;-5\right\}\\-1< x< \dfrac{2}{3}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x\in\left\{0;-2;4;-6\right\}\\-1< x< \dfrac{2}{3}\end{matrix}\right.\Leftrightarrow x=0\)
Thay x=0 vào B, ta được:
\(B=\dfrac{2-3\cdot0}{0+1}=\dfrac{2}{1}=2\) là số nguyên tố
Vậy: x=0


a: ĐKXĐ: \(n^2-2n\ne0\)
=>\(n\left(n-2\right)\ne0\)
=>\(n\notin\left\{0;2\right\}\)
b: Thay n=-3 vào A, ta được:
\(A=\dfrac{3}{\left(-3\right)^2-2\cdot\left(-3\right)}=\dfrac{3}{15}=\dfrac{1}{5}\)
Thay n=5 vào A, ta được:
\(A=\dfrac{3}{5^2-2\cdot5}=\dfrac{3}{25-10}=\dfrac{3}{15}=\dfrac{1}{5}\)

Câu 1:
\(\dfrac{1}{11}< \dfrac{1}{10}\)
\(\dfrac{1}{12}< \dfrac{1}{10}\)
...
\(\dfrac{1}{20}< \dfrac{1}{10}\)
Do đó: \(B=\dfrac{1}{11}+\dfrac{1}{12}+...+\dfrac{1}{20}< \dfrac{1}{10}+\dfrac{1}{10}+...+\dfrac{1}{10}=1\)(1)
\(\dfrac{1}{11}>\dfrac{1}{20}\)
\(\dfrac{1}{12}>\dfrac{1}{20}\)
...
\(\dfrac{1}{20}=\dfrac{1}{20}\)
Do đó: \(B=\dfrac{1}{11}+\dfrac{1}{12}+...+\dfrac{1}{20}>\dfrac{1}{20}+\dfrac{1}{20}+...+\dfrac{1}{20}=\dfrac{10}{20}=\dfrac{1}{2}\)
Suy ra: \(\dfrac{1}{2}< B< 1\)

a: Trên tia Ox, ta có: OM<ON
nên M nằm giữa O và N
=>OM+MN=ON
=>MN+2=6
=>MN=4(cm)
b: Vì OM<MN
nên M không là trung điểm của ON
c: Elà trung điểm của MN
=>\(EM=EN=\dfrac{MN}{2}=2\left(cm\right)\)
Vì MO và ME là hai tia đối nhau
nên M nằm giữa O và E
=>EO=MO+ME=2+2=4(cm)



\(\dfrac{1}{2^2}>\dfrac{1}{2\cdot3}=\dfrac{1}{2}-\dfrac{1}{3}\)
\(\dfrac{1}{3^2}>\dfrac{1}{3\cdot4}=\dfrac{1}{3}-\dfrac{1}{4}\)
...
\(\dfrac{1}{9^2}>\dfrac{1}{9\cdot10}=\dfrac{1}{9}-\dfrac{1}{10}\)
Do đó: \(A>\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{9}-\dfrac{1}{10}=\dfrac{1}{2}-\dfrac{1}{10}=\dfrac{4}{10}=\dfrac{2}{5}\)
\(\dfrac{1}{2^2}< \dfrac{1}{1\cdot2}=1-\dfrac{1}{2}\)
\(\dfrac{1}{3^2}< \dfrac{1}{2\cdot3}=\dfrac{1}{2}-\dfrac{1}{3}\)
...
\(\dfrac{1}{9^2}< \dfrac{1}{8\cdot9}=\dfrac{1}{8}-\dfrac{1}{9}\)
Do đó: \(A=\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{9^2}< 1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{8}-\dfrac{1}{9}=\dfrac{8}{9}\)
Suy ra: \(\dfrac{2}{5}< A< \dfrac{8}{9}\)

\(A=\dfrac{1}{3}+\dfrac{1}{3^2}+...+\dfrac{1}{3^{99}}\)
=>\(3A=1+\dfrac{1}{3}+...+\dfrac{1}{3^{98}}\)
=>\(3A-A=1+\dfrac{1}{3}+...+\dfrac{1}{3^{98}}-\dfrac{1}{3}-\dfrac{1}{3^2}-...-\dfrac{1}{3^{99}}\)
=>\(2A=1-\dfrac{1}{3^{99}}\)
=>\(A=\dfrac{1}{2}-\dfrac{1}{2\cdot3^{99}}< \dfrac{1}{2}\)
Bài 6:
a: \(\dfrac{3}{4}-x=1\)
=>\(x=\dfrac{3}{4}-1=-\dfrac{1}{4}\)
b: \(x+4=\dfrac{1}{5}\)
=>\(x=\dfrac{1}{5}-4\)
=>\(x=\dfrac{1}{5}-\dfrac{20}{5}=-\dfrac{19}{5}\)
c: \(x-\dfrac{1}{5}=2\)
=>\(x=2+\dfrac{1}{5}\)
=>\(x=\dfrac{11}{5}\)
d: \(\dfrac{x}{-5}=\dfrac{6}{-10}\)
=>\(\dfrac{x}{-5}=\dfrac{3}{-5}\)
=>x=3
Bài 7:
a: 2/3 của 27 là \(\dfrac{2}{3}\cdot27=18\)
b: 5/6 của 300 là \(300\cdot\dfrac{5}{6}=250\)
Bài 5:
e: \(\left(\dfrac{-2}{-5}+\dfrac{-5}{-6}\right)+\dfrac{4}{5}\)
\(=\left(\dfrac{2}{5}+\dfrac{5}{6}\right)+\dfrac{4}{5}\)
\(=\dfrac{6}{5}+\dfrac{5}{6}=\dfrac{61}{30}\)
f: \(\dfrac{5}{13}\cdot\dfrac{17}{26}+\dfrac{5}{13}\cdot\dfrac{9}{26}\)
\(=\dfrac{5}{13}\left(\dfrac{17}{26}+\dfrac{9}{26}\right)\)
\(=\dfrac{5}{13}\cdot\dfrac{26}{26}=\dfrac{5}{13}\)