a) \(0.25\in Q\) b) \(-\dfrac{6}{7}\in Q\) c) \(-235\notin Q\)
Hãy cho biết tính đúng, sai của mỗi khẳng định sau:
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b) Xét pt hoành độ giao điểm của hàm số đã cho và Ox là \(2x^3+2\left(6m-1\right)x^2-3\left(2m-1\right)x-3\left(1+2m\right)=0\) (*)
Ta thấy \(x=1\) là nghiệm của pt trên. Lập sơ đồ Horner:
| \(2\) | \(2\left(6m-1\right)\) | \(-3\left(2m-1\right)\) | \(-3\left(1+2m\right)\) | |
| \(x=1\) | \(2\) | \(12m\) | \(6m+3\) | \(0\) |
Do đó pt (*)
\(\Leftrightarrow\left(x-1\right)\left(2x^2+12mx+6m+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\2x^2+12mx+6m+3=0\end{matrix}\right.\)
Xét pt \(2x^2+12mx+6m+3=0\) (1)
Ycbt \(\Leftrightarrow\) pt (1) có 2 nghiệm phân biệt \(x_1,x_2\) khác 1 và thỏa mãn \(x_1^2+x_2^2=27\)
Có \(\Delta'=\left(6m\right)^2-2\left(6m+3\right)=36m^2-12m-6>0\)
\(\Leftrightarrow\left[{}\begin{matrix}m>\dfrac{1+\sqrt{7}}{6}\\m< \dfrac{1-\sqrt{7}}{6}\end{matrix}\right.\)
Có 2 nghiệm khác 1 \(\Leftrightarrow2.1^2+12m.1+6m+3\ne0\)
\(\Leftrightarrow18m+5\ne0\)
\(\Leftrightarrow m\ne-\dfrac{5}{18}\)
Theo định lý Vi-ét, ta có: \(\left\{{}\begin{matrix}x_1+x_2=-6m\\x_1x_2=\dfrac{6m+3}{2}\end{matrix}\right.\)
Để \(x_1^2+x_2^2=27\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=27\)
\(\Leftrightarrow\left(-6m\right)^2-2.\dfrac{6m+3}{2}=27\)
\(\Leftrightarrow36m^2-6m-3=27\)
\(\Leftrightarrow6m^2-m-5=0\)
\(\Leftrightarrow6m^2-6m+5m-5=0\)
\(\Leftrightarrow6m\left(m-1\right)+5\left(m-1\right)=0\)
\(\Leftrightarrow\left(m-1\right)\left(6m+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=1\left(nhận\right)\\m=-\dfrac{5}{6}\left(nhận\right)\end{matrix}\right.\)
Vậy \(m=1\) hoặc \(m=-\dfrac{5}{6}\) thỏa ycbt.
c) Xét pt \(x^3-3mx^2+\left(3m-1\right)x+6m=0\) (*)
Ta thấy (*) có nghiệm \(x=-1\). Lập sơ đồ Horner:
| \(1\) | \(-3m\) | \(3m-1\) | \(6m\) | |
| \(x=-1\) | \(1\) | \(-3m-1\) | \(6m\) | \(0\) |
Vậy (*) \(\Leftrightarrow\left(x+1\right)\left(x^2-\left(3m+1\right)x+6m\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x^2-\left(3m+1\right)x+6m=0\end{matrix}\right.\)
Tới đây thì làm tương tự câu b) nhé.

Mỗi kí tự có 10 cách chọn số, 26 cách chọn chữ in hoa và 26 cách chọn chữ in thường. Do đó mỗi kí tự có \(10+2.26=62\) cách chọn. Khi đó số mật khẩu có thể là \(62^{10}\)
Trong trường hợp xấu nhất, kẻ gian sẽ mất \(62^{10}\) giây, để cho gọn hơn thì là \(62^{10}:60:60:24:365:100=266140083\) thể kỷ
P/S: Đó là khi kẻ gian không chết trước khi phá được mật khẩu.

\(1+2+3+...+x=55\)
=>\(x\cdot\dfrac{\left(x+1\right)}{2}=55\)
=>x(x+1)=110
=>\(x^2+x-110=0\)
=>(x+11)(x-10)=0
=>\(\left[{}\begin{matrix}x+11=0\\x-10=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-11\left(loại\right)\\x=10\left(nhận\right)\end{matrix}\right.\)
Vậy: x=10
\(1+2+3+...+x=55\)
\(\dfrac{x\left(x+1\right)}{2}=55\)
\(x\left(x+1\right)=2\cdot55=110\)
\(x^2+x-110=0\)
\(x^2-10x+11x-110=0\\ x\left(x-10\right)+11\left(x-10\right)=0\\ \left(x-10\right)\left(x+11\right)=0\\ \left[{}\begin{matrix}x=10\\x=-11\end{matrix}\right.\)

\(\dfrac{40404}{70707}-\dfrac{1}{14}\\ =\dfrac{4\cdot10101}{7\cdot10101}-\dfrac{1}{14}\\ =\dfrac{4}{7}-\dfrac{1}{14}\\ =\dfrac{8}{14}-\dfrac{1}{14}\\ =\dfrac{7}{14}\\ =\dfrac{1}{2}\)

a: Xét ΔBAE vuông tại A và ΔBHE vuông tại H có
BE chung
\(\widehat{ABE}=\widehat{HBE}\)
Do đó: ΔBAE=ΔBHE
b: ΔBAE=ΔBHE
=>BA=BH và EA=EH
Ta có: BA=BH
=>B nằm trên đường trung trực của AH(1)
Ta có: EA=EH
=>E nằm trên đường trung trực của AH(2)
Từ (1),(2) suy ra BE là đường trung trực của AH
c: Xét ΔEAK vuông tại A và ΔEHC vuông tại H có
EA=EH
\(\widehat{AEK}=\widehat{HEC}\)
Do đó: ΔEAK=ΔEHC
=>EK=EC
mà EK>EA(ΔEAK vuông tại A)
nên EC>EA


\(\dfrac{40404}{70707}-\dfrac{1}{14}\)
\(=\dfrac{4}{7}-\dfrac{1}{14}\)
\(=\dfrac{8}{14}-\dfrac{1}{14}=\dfrac{7}{14}=\dfrac{1}{2}\)

a: BE=BD+DE
CD=CE+DE
mà BD=CE
nên BE=CD
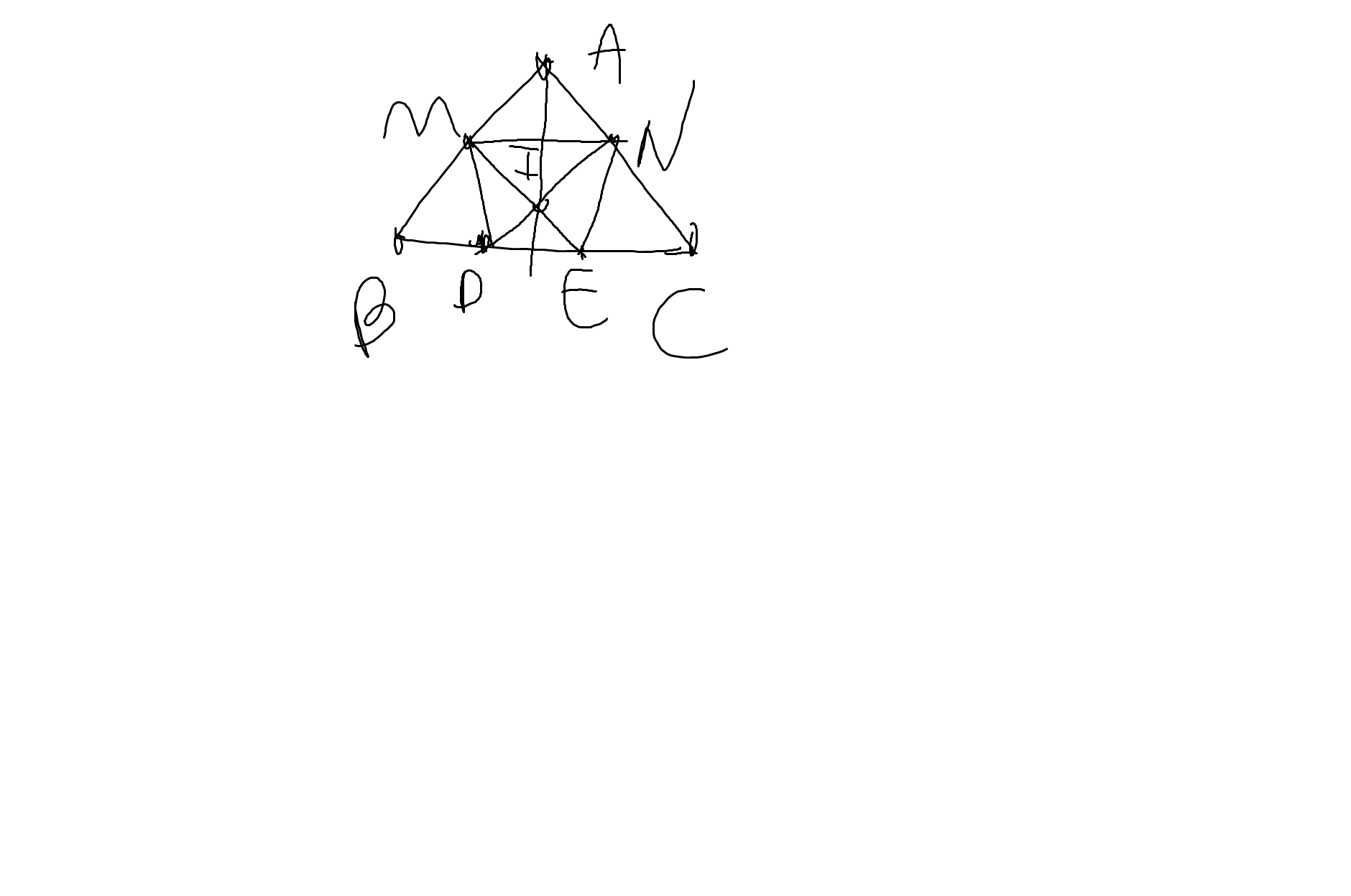
Ta có: \(AM=MB=\dfrac{AB}{2}\)
\(AN=NC=\dfrac{AC}{2}\)
mà AB=AC
nên AM=MB=AN=NC
Xét ΔMBE và ΔNCD có
MB=NC
\(\widehat{MBE}=\widehat{NCD}\)
BE=CD
Do đó: ΔMBE=ΔNCD
=>ME=ND
b:
Xét ΔABC có \(\dfrac{AM}{AB}=\dfrac{AN}{AC}\)
nên MN//BC
=>MN//DE
Xét tứ giác MNED có
MN//ED
ME=ND
Do đó: MNED là hình bình hành
=>MD=NE
Xét ΔMDE và ΔNED có
MD=NE
DE chung
ME=ND
Do đó: ΔMDE=ΔNED
=>\(\widehat{MED}=\widehat{NDE}\)
=>\(\widehat{IDE}=\widehat{IED}\)
=>ΔIED cân tại I
c: Ta có: \(\widehat{IDE}+\widehat{IDB}=180^0\)(hai góc kề bù)
\(\widehat{IED}+\widehat{IEC}=180^0\)(hai góc kề bù)
mà \(\widehat{IDE}=\widehat{IED}\)
nên \(\widehat{IDB}=\widehat{IEC}\)
Xét ΔIDB và ΔIEC có
ID=IE
\(\widehat{IDB}=\widehat{IEC}\)
DB=EC
Do đó: ΔIDB=ΔIEC
=>IB=IC
=>I nằm trên đường trung trực của BC(1)
ta có: AB=AC
=>A nằm trên đường trung trực của BC(2)
Từ (1),(2) suy ra AI là đường trung trực của BC
=>AI\(\perp\)BC
a: \(0,25\in Q\)
=>Đúng
b: \(-\dfrac{6}{7}\in Q\)
=>Đúng
c: \(-235\notin Q\)
=>Sai