CM rằng BT luôn dương với mọi giá trị
a) x^2-x+1>0 với mọi x
b)4x^2+y^2-z^2-4x-2z+2y+2014>0 với mọi x;y;z
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(1-2+3-4+5-6+...+2019-2020+2021\)
\(=\left(1-2\right)+\left(3-4\right)+\left(5-6\right)+...+\left(2019-2020\right)+2021\)
\(=-1-1-1-..-1+2021\)
\(=-1\cdot1010+2021\)
\(=-1010+2021\)
\(=-1011\)
1−2+3−4+5−6+...+2019−2020+2021
=(1−2)+(3−4)+(5−6)+...+(2019−2020)+2021=(1−2)+(3−4)+(5−6)+...+(2019−2020)+2021
=−1−1−1−..−1+2021=−1−1−1−..−1+2021
=−1⋅1010+2021=−1⋅1010+2021
=−1010+2021=−1010+2021
=−1011=−1011

\(1000=2^3\cdot5^3\)
\(7200=2^5\cdot3^2\cdot5^2\)
\(810=2\cdot3^4\cdot5\)
\(8000=2^6\cdot5^3\)

1.
$3x^4-48=3(x^4-16)=3[(x^2)^2-4^2]=3(x^2-4)(x^2+4)$
$=3(x-2)(x+2)(x^2+4)$
2.
$x^3-4x^2+8x-8=(x^3-8)-(4x^2-8x)$
$=(x-2)(x^2+2x+4)-4x(x-2)=(x-2)(x^2+2x+4-4x)=(x-2)(x^2-2x+4)$
3.
$x^4-27x=x(x^3-27)=x(x^3-3^3)=x(x-3)(x^2+3x+9)$
4.
$x^4-x^3+x^2-1=(x^4-x^3)+(x^2-1)=x^3(x-1)+(x-1)(x+1)$
$=(x-1)(x^3+x+1)$
5.
$x^5+x^3-x^2-1=(x^5+x^3)-(x^2+1)=x^3(x^2+1)-(x^2+1)$
$=(x^2+1)(x^3-1)=(x^2+1)(x-1)(x^2+x+1)$
6.
$x^3+2x^2+2x+1=(x^3+x^2)+(x^2+2x+1)=x^2(x+1)+(x+1)^2$
$=(x+1)(x^2+x+1)$
7.
$x^3+x^2-4x-4=(x^3+x^2)-(4x+4)=x^2(x+1)-4(x+1)$
$=(x+1)(x^2-4)=(x+1)(x-2)(x+2)$
8.
$x^4-2x^3+2x-1=(x^4-2x^3+x^2)-(x^2-2x+1)$
$=(x^2-x)^2-(x-1)^2=x^2(x-1)^2-(x-1)^2=(x-1)^2(x^2-1)=(x-1)^2(x-1)(x+1)$


Lời giải:
Số hsg là: $32.\frac{1}{4}=8$ (hs)
Số hsk là: $(32-8).\frac{3}{8}=9$ (hs)
Số hstb là: $32-8-9=15$ (hs)

81975 = (84)493.83 = \(\overline{..6}\)493. \(\overline{...2}\) = \(\overline{..2}\)

Lời giải:
a. $A=3xy(x^2+2xy+y^2)=3xy(x+y)^2=3.\frac{1}{2}.\frac{-1}{3}(\frac{1}{2}+\frac{-1}{3})^2=\frac{-1}{72}$
b.
$B=(-1)^2.3^2+(-1).3+(-1)^3+3^3=32$
c.
$D=5^2+4.5.1-3.1^3=42$
d.
$D=2xy(x+y)=2.1(-3)(1-3)=12$
e.
$M=\frac{(x+2)(2x-1)}{x+2}=2x-1=2(-1)-1=-3$
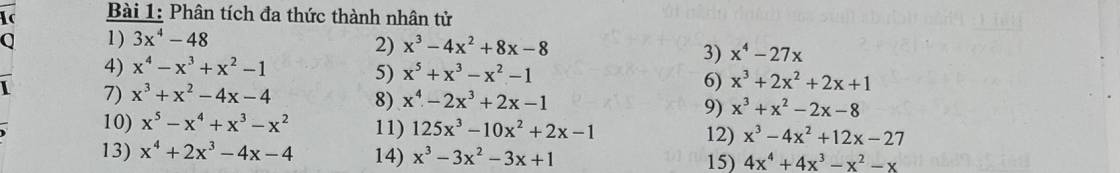
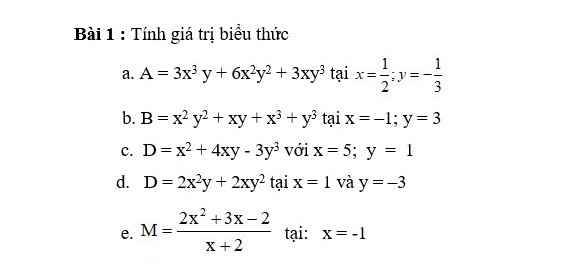
a) Ta có:
\(x^2-x+1\)
\(=x^2-2\cdot\dfrac{1}{2}\cdot x+\dfrac{1}{4}+\dfrac{3}{4}\)
\(=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\)
Mà: \(\left(x-\dfrac{1}{2}\right)^2\ge0\) và \(\dfrac{3}{4}>0\) nên
\(\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\forall x\)
\(\Rightarrow x^2-x+1>0\forall x\)