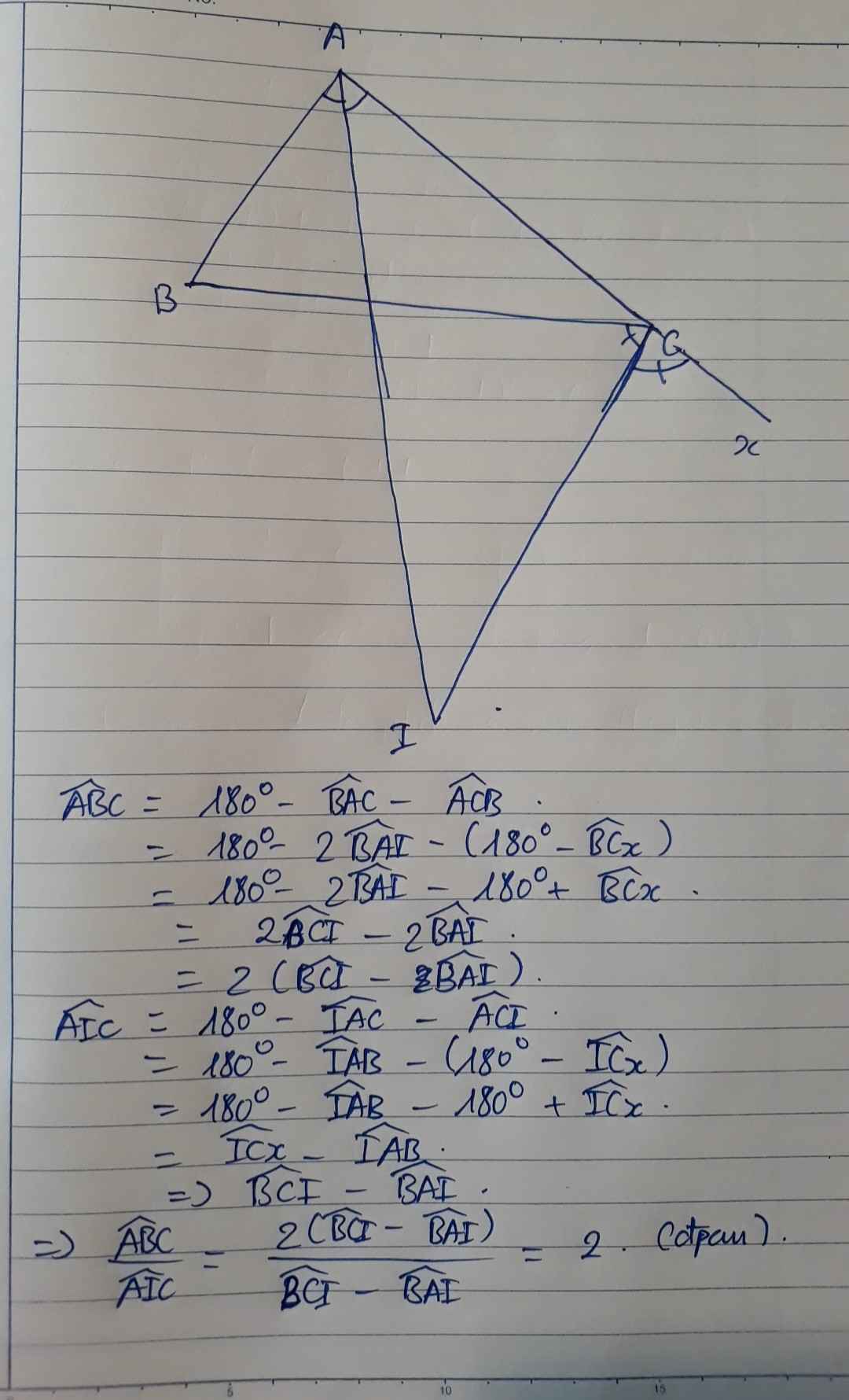
Ta có: 

\(5y=7z+5z=-30\\ =>5y=12z=-30\\ =>\left\{{}\begin{matrix}5y=-30\\12z=-30\end{matrix}\right.\\ =>\left\{{}\begin{matrix}y=-\dfrac{30}{5}=-6\\z=-\dfrac{30}{12}=-\dfrac{5}{2}\end{matrix}\right.\)  

\(2x=3y=3\cdot\left(-6\right)=-18\\ =>x=\dfrac{-18}{2}=-9\)

Vậy: ... 

\(5^{\left(x-1\right)\left(x+2\right)}=2024^0\\ =>5^{\left(x-1\right)\left(x+2\right)}=1\\ =>5^{\left(x-1\right)\left(x+2\right)}=5^0\\ =>\left(x-1\right)\left(x+2\right)=0\\ TH1:x-1=0\\ =>x=1\\ TH2:x+2=0\\ =>x=-2\)

Vậy: ... 

bằng 7 295 000 bạn nhé

`7,295`

Chữ số hàng phần chục nghìn là 5 nên làm tròn chữ số trước đó lên 1 đơn vị và toàn bộ các chữ số còn lại ở bên phải đều trở thành số 0

`(x-3)^5 : 2 = 6^4 . 3`

`=> (x-3)^5 : 2 = 6^4 . 3`

`=> (x-3)^5= 6^4 . 3 . 2`

`=> (x-3)^5= 6^4 . 6`

`=> (x-3)^5= 6^5`

`=> x - 3 = 6`

`=> x = 6+3`

`=> x = 9`

Vậy `x = 9`

\(\left(x-3\right)^5:2=6^4\cdot3\\ =>\left(x-3\right)^5=6^4\cdot3\cdot2\\ =>\left(x-3\right)^5=6^4\cdot6\\ =>\left(x-3\right)^5=6^5\\ =>x-3=6\\ =>x=6+3\\ =>x=9\)

Vậy: ... 

\(a.\left(x+1\right)^3=\left(x+1\right)^6\\ =>\left(x+1\right)^6-\left(x+1\right)^3=0\\ =>\left(x+1\right)^3\left[\left(x+1\right)^3-1\right]=0\\ TH1:\left(x+1\right)^3=0\\ =>x+1=0\\ =>x=-1\\ TH2:\left(x+1\right)^3-1=0\\ =>\left(x+1\right)^3=1\\ =>\left(x+1\right)^3=1^3\\ =>x+1=1\\ =>x=1-1=0\\ b.x^5=x\\ =>x^5-x=0\\ =>x\left(x^4-1\right)=0\\ TH1:x=0\\ TH2:x^4-1=0\\ =>x^4=1\\ =>x^4=\left(\pm1\right)^4\\ =>x=\pm4\)

a) Ta có: 

\(\dfrac{x^{12}}{x^9}=x^{12-9}=x^3\\ =>x^{12}=x^3\cdot x^9\)

b) Ta có:

\(x^{12}=x^{3\cdot4}=\left(x^3\right)^4\)

c) Ta có: 

\(\dfrac{x^{15}}{x^{12}}=x^{15-12}=x^3\\ =>x^{12}=\dfrac{x^{15}}{x^3}\)

a) \(x^{12}=x^{9+3}=x^9.x^3\)

b) \(x^{12}=x^{4.3}=\left(x^4\right)^3\)

c) \(x^{12}=x^{15-3}=x^{15}:x^3\)

a: Xét ΔAMB và ΔAMC có

AM chung

MB=MC

AB=AC

Do đó: ΔAMB=ΔAMC

b: ΔAMB=ΔAMC

=>\(\widehat{AMB}=\widehat{AMC}\)

mà \(\widehat{AMB}+\widehat{AMC}=180^0\)(hai góc kề bù)

nên \(\widehat{AMB}=\widehat{AMC}=\dfrac{180^0}{2}=90^0\)

=>AD\(\perp\)BC tại M

Xét ΔMAB vuông tại M và ΔMDC vuông tại M có

MA=MD

MB=MC

Do đó: ΔMAB=ΔMDC
=>\(\widehat{MAB}=\widehat{MDC}\)

=>AB//DC

c: ta có: ME\(\perp\)AB

AB//CD

Do đó: ME\(\perp\)CD

mà MF\(\perp\)CD

và ME,MF có điểm chung là M
nên M,E,F thẳng hàng

Xét ΔMEB vuông tại E và ΔMFC vuông tại F có

MB=MC

\(\widehat{MBE}=\widehat{MCF}\)(cmt)

Do đó: ΔMEB=ΔMFC

=>ME=MF

=>M là trung điểm của EF

`(2x+3)^2 =` \(\dfrac{9}{121}\)

`=> (2x + 3)^2 =` \(\left(\dfrac{3}{11}\right)^2\)

=> \(\left[{}\begin{matrix}2x+3=\dfrac{3}{11}\\2x+3=-\dfrac{3}{11}\end{matrix}\right.\)

=> \(\left[{}\begin{matrix}2x=\dfrac{3}{11}-3\\2x=-\dfrac{3}{11}-3\end{matrix}\right.\)

=> \(\left[{}\begin{matrix}2x=\dfrac{3}{11}-\dfrac{33}{11}\\2x=-\dfrac{3}{11}-\dfrac{33}{11}\end{matrix}\right.\)

=> \(\left[{}\begin{matrix}2x=-\dfrac{30}{11}\\2x=-\dfrac{36}{11}\end{matrix}\right.\)

=> \(\left[{}\begin{matrix}x=-\dfrac{15}{11}\\x=-\dfrac{18}{11}\end{matrix}\right.\)

Vậy ...

\(\left(2x+3\right)^2=\dfrac{9}{121}\)

\(\left(2x+3\right)^2=\left(\dfrac{3}{11}\right)^2\)

\(2x+3=\dfrac{2}{11}\) hoặc \(2x+3=-\dfrac{2}{11}\)

\(2x=-\dfrac{31}{11}\) hoặc \(2x=-\dfrac{35}{11}\)

\(x=-\dfrac{31}{22}\) hoặc \(x=-\dfrac{35}{22}\)