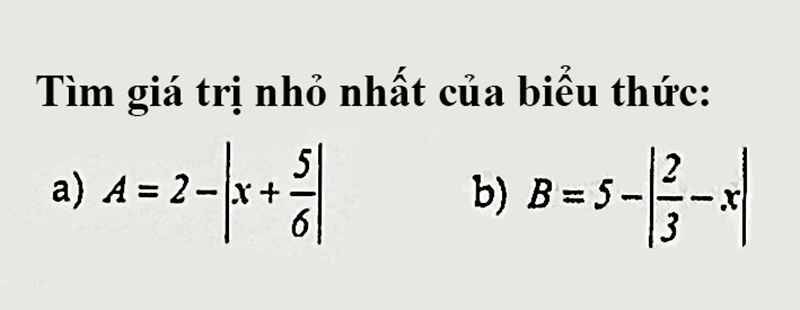
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(\left(3-x\right)^3=-\dfrac{27}{64}\)
\(\left(3-x\right)^3=\left(\dfrac{-3}{4}\right)^3\)
\(=>3-x=\dfrac{-3}{4}\)
\(x=3-\dfrac{-3}{4}=\dfrac{12}{4}+\dfrac{3}{4}\)
\(x=\dfrac{15}{4}\)
________
\(\left(x-5\right)^3=\dfrac{1}{-27}\)
\(\left(x-5\right)^3=\left(\dfrac{-1}{3}\right)^3\)
\(=>x-5=\dfrac{-1}{3}\)
\(x=\dfrac{-1}{3}+5=\dfrac{-1}{3}+\dfrac{15}{3}\)
\(x=\dfrac{14}{3}\)
_____________
\(\left(x-\dfrac{1}{2}\right)^3=\dfrac{27}{8}\)
\(\left(x-\dfrac{1}{2}\right)^3=\left(\dfrac{3}{2}\right)^3\)
\(=>x-\dfrac{1}{2}=\dfrac{3}{2}\)
\(x=\dfrac{3}{2}+\dfrac{1}{2}\)
\(x=2\)
________
\(\left(2x-1\right)^2=\dfrac{1}{4}\)
\(\left(2x-1\right)^2=\left(\dfrac{1}{2}\right)^2\) hoặc \(\left(2x-1\right)^2=\left(\dfrac{-1}{2}\right)^2\)
\(=>2x-1=\dfrac{1}{2}\) \(2x-1=\dfrac{-1}{2}\)
\(2x=\dfrac{1}{2}+1=\dfrac{1}{2}+\dfrac{2}{2}\) \(2x=\dfrac{-1}{2}+1=\dfrac{-1}{2}+\dfrac{2}{2}\)
\(2x=\dfrac{3}{2}\) \(2x=\dfrac{1}{2}\)
\(x=\dfrac{3}{2}:2=\dfrac{3}{2}.\dfrac{1}{2}\) \(x=\dfrac{1}{2}:2=\dfrac{1}{2}.\dfrac{1}{2}\)
\(x=\dfrac{3}{4}\) \(x=\dfrac{1}{4}\)
____________
\(\left(2-3x\right)^2=\dfrac{9}{4}\)
\(\left(2-3x\right)^2=\left(\dfrac{3}{2}\right)^2\) hoặc \(\left(2-3x\right)^2=\left(\dfrac{-3}{2}\right)^2\)
\(=>2-3x=\dfrac{3}{2}\) \(2-3x=\dfrac{-3}{2}\)
\(3x=2-\dfrac{3}{2}=\dfrac{4}{2}-\dfrac{3}{2}\) \(3x=2-\dfrac{-3}{2}=\dfrac{4}{2}+\dfrac{3}{2}\)
\(3x=\dfrac{1}{2}\) \(3x=\dfrac{7}{2}\)
\(x=\dfrac{1}{2}.\dfrac{1}{3}\) \(x=\dfrac{7}{2}.\dfrac{1}{3}\)
\(x=\dfrac{1}{6}\) \(x=\dfrac{7}{6}\)
______________
\(\left(1-\dfrac{2}{3}\right)^2=\dfrac{4}{9}\) -> Kiểm tra đề câu này
(3-x)3=(-\(\dfrac{3}{4}\))3
3-x=-\(\dfrac{3}{4}\)
x=3-(-\(\dfrac{3}{4}\))
x=\(\dfrac{15}{4}\)

a, (3 + x)2 = 4
(3 + x)2 = 22 = (-2)2
TH1: 3 + x = 2
x = 2 - 3
x = -1
TH2: 3 + x = -2
x = -2 - 3
x = -2 + (-3)
x = -5
Vậy x ϵ {-1; -5}
b, (2x + 1) 3 = -8
(2x + 1)3 = (-2)3
2x + 1 = -2
2x = -2 - 1
2x = -2 + (-1)
2x = -3
x = \(\dfrac{-3}{2}\)

`#3107.101107`
\(\dfrac{5}{7}\times\dfrac{6}{11}+\dfrac{5}{11}\times\dfrac{1}{7}-\dfrac{5}{7}\times\dfrac{14}{11}\\ =\dfrac{5}{7}\times\dfrac{6}{11}+\dfrac{5}{7}\times\dfrac{1}{11}-\dfrac{5}{7}\times\dfrac{14}{11}\\ =\dfrac{5}{7}\times\left(\dfrac{6}{11}+\dfrac{1}{11}-\dfrac{14}{11}\right)\\ =\dfrac{5}{7}\times\left(-\dfrac{7}{11}\right)\\ =-\dfrac{5}{11}\)

\(\dfrac{5}{7}\cdot\dfrac{6}{11}+\dfrac{5}{11}\cdot\dfrac{1}{7}-\dfrac{5}{7}\cdot\dfrac{14}{11}\)
\(=\dfrac{5}{7}\cdot\dfrac{6}{11}+\dfrac{5}{7}\cdot\dfrac{1}{11}-\dfrac{5}{7}\cdot\dfrac{14}{11}\)
\(=\dfrac{5}{7}\cdot\left(\dfrac{6}{11}+\dfrac{1}{11}-\dfrac{14}{11}\right)\)
\(=\dfrac{5}{7}\cdot\dfrac{-7}{11}=\dfrac{-5}{11}\)

`(x-1)^3=1/8`
<=> `(x-1)^3=(1/2)^3`
<=> `x-1=1/2`
<=> `x=1/2` `+ 1`
<=> `x=3/2`

`#3107.101107`
\(\dfrac{27^2\cdot2^3\cdot5^4}{15^2\cdot6^9}\)
\(=\dfrac{\left(3^3\right)^2\cdot2^3\cdot5^4}{3^2\cdot5^2\cdot2^9\cdot3^9}\)
\(=\dfrac{3^6\cdot2^3\cdot5^4}{3^{11}\cdot5^2\cdot2^9}\)
\(=\dfrac{5^2}{3^5\cdot2^6}\)
\(=\dfrac{25}{15552}\)
\(A=2-\left|x+\dfrac{5}{6}\right|\\ Mà:\left|x+\dfrac{5}{6}\right|\ge0\forall x\in R\\ Vây:max_A=2.khi.x+\dfrac{5}{6}=0\Leftrightarrow x=-\dfrac{5}{6}\)
B làm tương tự, nhưng mình nghĩ là tìm max chứ min thì cái biểu thực GTTĐ luôn không âm mà như thế thì nhỏ vô tận luôn í
cả hai câu sai đề, A và B không có GTNN