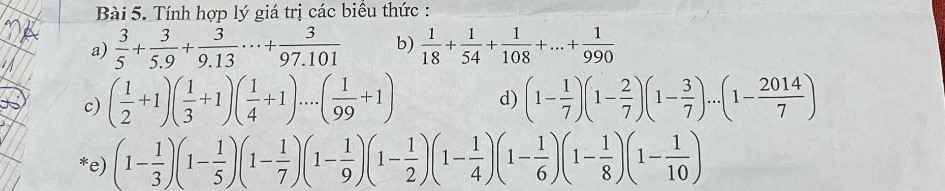a: \(\dfrac{3}{5}+\dfrac{3}{5\cdot9}+...+\dfrac{3}{97\cdot101}\)

\(=\dfrac{3}{4}\left(\dfrac{4}{1\cdot5}+\dfrac{4}{5\cdot9}+...+\dfrac{4}{97\cdot101}\right)\)

\(=\dfrac{3}{4}\left(1-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{9}+...+\dfrac{1}{97}-\dfrac{1}{101}\right)\)

\(=\dfrac{3}{4}\left(1-\dfrac{1}{101}\right)=\dfrac{3}{4}\cdot\dfrac{100}{101}=\dfrac{75}{101}\)

b: \(\dfrac{1}{18}+\dfrac{1}{54}+\dfrac{1}{108}+...+\dfrac{1}{990}\)

\(=\dfrac{1}{3\cdot6}+\dfrac{1}{6\cdot9}+...+\dfrac{1}{30\cdot33}\)

\(=\dfrac{1}{3}\left(\dfrac{3}{3\cdot6}+\dfrac{3}{6\cdot9}+...+\dfrac{3}{30\cdot33}\right)\)

\(=\dfrac{1}{3}\left(\dfrac{1}{3}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{9}+...+\dfrac{1}{30}-\dfrac{1}{33}\right)\)

\(=\dfrac{1}{3}\cdot\left(\dfrac{1}{3}-\dfrac{1}{33}\right)=\dfrac{1}{3}\cdot\dfrac{10}{33}=\dfrac{10}{99}\)

c: \(\left(\dfrac{1}{2}+1\right)\left(\dfrac{1}{3}+1\right)\cdot...\cdot\left(\dfrac{1}{99}+1\right)\)

\(=\dfrac{3}{2}\cdot\dfrac{4}{3}\cdot...\cdot\dfrac{100}{99}=\dfrac{100}{2}=50\)

d: \(\left(1-\dfrac{1}{7}\right)\left(1-\dfrac{2}{7}\right)\cdot...\cdot\left(1-\dfrac{2014}{7}\right)\)

\(=\left(1-\dfrac{7}{7}\right)\cdot\dfrac{6}{7}\cdot\dfrac{5}{7}\cdot...\cdot\dfrac{-2007}{7}\)

\(=\left(1-1\right)\cdot\dfrac{6}{7}\cdot\dfrac{5}{7}\cdot...\cdot\dfrac{-2007}{7}\)

=0

\(A=\dfrac{5}{40}+\dfrac{5}{88}+\dfrac{5}{154}+\dfrac{5}{238}+\dfrac{5}{340}\)

\(=\dfrac{5}{5\cdot8}+\dfrac{5}{8\cdot11}+\dfrac{5}{11\cdot14}+\dfrac{5}{14\cdot17}+\dfrac{5}{17\cdot20}\)

\(=\dfrac{5}{3}\left(\dfrac{3}{5\cdot8}+\dfrac{3}{8\cdot11}+\dfrac{3}{11\cdot14}+\dfrac{3}{14\cdot17}+\dfrac{3}{17\cdot20}\right)\)

\(=\dfrac{5}{3}\left(\dfrac{1}{5}-\dfrac{1}{8}+\dfrac{1}{8}-\dfrac{1}{11}+...+\dfrac{1}{17}-\dfrac{1}{20}\right)\)

\(=\dfrac{5}{3}\left(\dfrac{1}{5}-\dfrac{1}{20}\right)=\dfrac{5}{3}\cdot\dfrac{3}{20}=\dfrac{1}{4}\)

\(\dfrac{x+2}{3}=\dfrac{x-4}{5}\)

=>5(x+2)=3(x-4)

=>5x+10=3x-12

=>5x-3x=-12-10

=>2x=-22

=>\(x=-\dfrac{22}{2}=-11\)

\(x+\dfrac{4}{5\cdot9}+\dfrac{4}{9\cdot13}+...+\dfrac{4}{41\cdot45}=\dfrac{29}{45}\)

=>\(x+\dfrac{1}{5}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{13}+...+\dfrac{1}{41}-\dfrac{1}{45}=\dfrac{29}{45}\)

=>\(x+\dfrac{1}{5}-\dfrac{1}{45}=\dfrac{29}{45}\)

=>\(x+\dfrac{8}{45}=\dfrac{29}{45}\)

=>\(x=\dfrac{29-8}{45}=\dfrac{21}{45}=\dfrac{7}{15}\)

1: (x-2)(y+3)=11

=>\(\left(x-2\right)\left(y+3\right)=1\cdot11=11\cdot1=\left(-1\right)\cdot\left(-11\right)=\left(-11\right)\cdot\left(-1\right)\)

=>\(\left(x-2;y+3\right)\in\left\{\left(1;11\right);\left(11;1\right);\left(-1;-11\right);\left(-11;-1\right)\right\}\)

=>\(\left(x,y\right)\in\left\{\left(3;8\right);\left(13;-2\right);\left(1;-14\right);\left(-9;-4\right)\right\}\)

2: \(xy+3x-7y-21=0\)

=>\(x\left(y+3\right)-7\cdot\left(y+3\right)=0\)

=>(y+3)(x-7)=0

=>\(\left\{{}\begin{matrix}x-7=0\\y+3=0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x=7\\y=-3\end{matrix}\right.\)

1, (y + 3) . (x - 2) = 11
Vì x, y ϵ Z
⇒ (y + 3); (x - 2) ϵ Z
⇒ (y + 3); (x - 2) ϵ Ư(11) = {1; -1; 11; -11}
Lập bảng

Vậy (x; y) ϵ {(13; -2); (-9; -4); (3; 8); (1; -14)}

2, xy + 3x - 7y - 21 = 0
x(y + 3) - (7y + 21) = 0
x(y + 3) - 7(y + 3) = 0
(y + 3)(x - 7) = 0
⇒ y + 3 = 0; x - 7 = 0
y = -3; x = 7

(Bạn có thể tự sửa bài nhá)

=1/10-1/11+1/12-1/13+.....+1/49-1/50

=1/10-1/50

=2/25

Mn cứu em vs:(

Bạn cần ghi đầy đủ đề để mọi người hỗ trợ tốt hơn nhé.

Lời giải:

Vì $n,n+1$ là hai số nguyên liên tiếp nên một trong hai số là số chẵn, một số là số lẻ.

$\Rightarrow n(n+1)\vdots 2$

$\Rightarrow n(n+1)(n-10)\vdots 2(1)$

Mặt khác:

Nếu $n$ chia hết cho 3 thì $n(n+1)(n-10)\vdots 3$

Nếu $n$ chia 3 dư 1. Đặt $n=3k+1$ với $k$ nguyên thì $n-10=3k-9=3(k-3)\vdots 3$

$\Rightarrow n(n+1)(n-10)\vdots 3$

Nếu $n$ chia 3 dư 2. Đặt $n=3k+2$ với $k$ nguyên thì $n+1=3k+3=3(k+1)\vdots 3$

$\Rightarrow n(n+1)(n-10)\vdots 3$
Vậy $n(n+1)(n-10)\vdots 3$ với mọi $n$ nguyên (2)

Từ $(1); (2)$ mà $(2,3)=1$ nên $n(n+1)(n-10)\vdots (2.3)$ hay $n(n+1)(n-10)\vdots 6$