\(\hept{\begin{cases}x-\left(m+3\right)y=0\\\left(m-2\right)x+4y=m-1\end{cases}}\)
Tìm m để hệ trên vô nghiệm
Cho \(a^2+b^2+16=8a+6b\)Tìm Max S = \(4a+3b\)
Hai phương trình \(x^2+ax+1=0\)và \(x^2-x-a=0\)có nghiệm chung khi đó a =....
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

đường tròn nội típ của một tam giác vuông sẽ có đường kinh bằng cạnh huyền của tam giác vuông ý nhé :D
CM:
Gọi △ABC△ABC vuông tại A
Gọi M là trung điểm của AC
vẽ đường thẳng Md⊥ABMd⊥AB cắt BC tại H
dể dang cm được MHMH là đường trung bình =>BH=HC=>BH=HC
hay đường trung trực của BC cắt BC tại H
=> H là giao điểm của 3 đường trung trực △ABC△ABC
=>=> đường tròn nội típ △ABC△ABC có bán kính là BHBH hay HCHC
=>BC=82+152−−−−−−−√=17=>BC=82+152=17
=>BH=r=8,5
p/s : kham khảo
Công thức tính bán kính đường tròn ngoại tiếp tam giác thường sẽ là:
\(R=\frac{abc}{4S}\)
Trong đó:
Ngoài ra, đối với đa giác đều có độ dài mỗi cạnh là a, ta có công thức tính
bán kính đường tròn ngoại tiếp đa giác sẽ là:
\(R=\frac{a}{2}\left(\frac{\sin180^o}{n}\right)\)

Giả sử 4 xe tải nhỏ mỗi xe tăng thêm 3 tấn, tức là tương đương có thêm 12 kg và thêm 4 xe tải lớn. Khi đó, tổng số tấn hàng là 178 + 12 = 190 tấn, tương ứng với 15 +4 = 19 xe tải lớn. Vậy, mỗi xe tải lớn chở 190 : 19 = 10 (tấn) và xe tải nhỏ chở 10 - 3 = 7 ( tấn).
Check: 15 * 10 + 4 * 7 = 178 (tấn)
Thêm 12 tấn hàng bạn nhé. Quen tay đánh nhầm thành kg :D

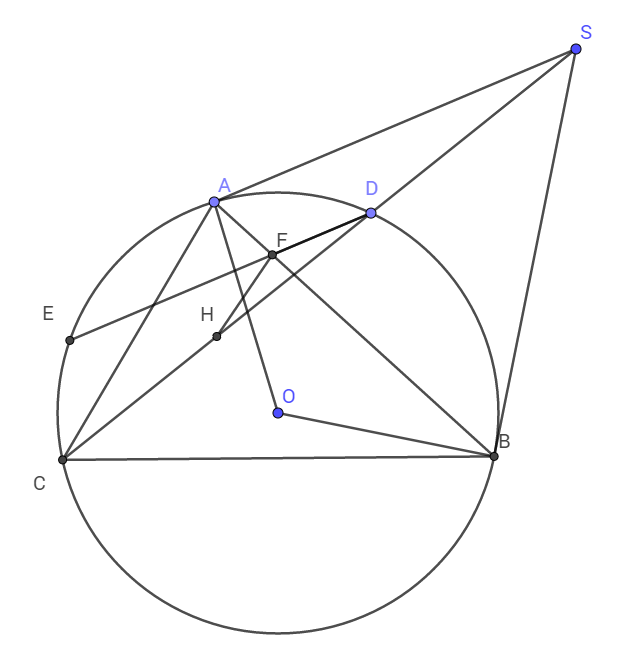
Ta có các tam giác vuông AOS; HOS, BOS có chung cạnh huyền OS nên S, A, H, O, B nội tiếp đường tròn đường kính OS.
Khi đó ta có :
\(\widehat{ASH}=\widehat{ABH}\) (Hai góc nội tiếp cùng chắn cung AH)
Mà \(\widehat{ASH}=\widehat{FDH}\) (Hai góc đồng vị)
\(\Rightarrow\widehat{ABH}=\widehat{FDH}\)
Suy ra tứ giác HFDO nội tiếp.
Từ đó ta có \(\widehat{FHD}=\widehat{ABD}\)(Hai góc nội tiếp)
Mà \(\widehat{ABD}=\widehat{ACD}\) (Hai góc nội tiếp)
Nên \(\widehat{FHD}=\widehat{ACD}\)
Chúng lại ở vị trí đồng vị nên HF // AC.


Áp dụng bất đẳng thức Cô si cho ba số dương ta có \(a+b+c\ge3\sqrt[3]{abc}\) và \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\ge\frac{3}{\sqrt[3]{abc}}\). Do đó nếu đặt \(t=\sqrt[3]{abc}\) t hì \(a+b+c+\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\ge3\left(t+\frac{1}{t}\right)\) . Chú ý rằng từ giả thiết
\(\frac{a}{bc}+\frac{b}{ca}+\frac{c}{ab}=1\) suy ra \(a^2+b^2+c^2=abc\) từ đó
\(abc=a^2+b^2+c^2\ge3\sqrt[3]{a^2b^2c^2}\Rightarrow a^3b^3c^3\ge27a^2b^2c^2\Rightarrow abc\ge27\)\(\Rightarrow t\ge3\).
Do đó \(t+\frac{1}{t}=\frac{8t}{9}+\frac{t}{9}+\frac{1}{t}\ge\frac{8.3}{9}+2\sqrt{\frac{t}{9}.\frac{1}{t}}=\frac{10}{3}\). Suy ra
\(a+b+c+\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\ge3\left(t+\frac{1}{t}\right)\ge\frac{3.10}{3}=10\)
Đẳng thức xảy ra khi và chỉ khi \(\hept{\begin{cases}a=b=c>0\\t=\sqrt[3]{abc}=3\\a^2+b^2+c^2=abc\end{cases}}\)\(\Leftrightarrow a=b=c=3\).
