Gọi J là giao điểm của BP và KE; Xét \(\Delta\)BSJ có:

PE // BS; PE = \(\dfrac{1}{2}\) BS 

⇒ PF là đường trung bình của \(\Delta\)BSJ (vì đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy)

⇒ PJ = PB;  EJ = ES (1)

Xét \(\Delta\)ABJ có: AF = FB (gt); PJ = PB  theo (1)

⇒  PF là đường trung bình của \(\Delta\) ABJ (vì đường trung bình của tam giác đi qua trung điểm hai cạnh của tam giác và song song với cạnh còn lại)

 ⇒ PF// AJ  (2) 

Xét tứ giác ASCJ ta có: E là giao điểm hai đường chéo

     AE = EC (gt)

    EJ = ES ( theo (1)

⇒ Tứ giác ASCJ là hình bình hành vì tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường thì tứ giác đó là hình bình hành.

⇒ CS // CJ (3)

Kết hợp (2) và(3) ta có:

     CS // PF ( vì trong cùng một mặt phẳng hai đường thẳng cùng song song với đường thẳng thứ ba thì song song với nhau.)

  Kết luận: nếu BS = 2EP thì  CS // PF điều phải chứng minh

3 = 3

4 = 2²

10 = 2.5

BCNN(3; 4; 10) = 2².3.5 = 60

Các bội nhỏ hơn 200 của 3; 4; 10 là:

BC(3; 4; 10) = {0; 60; 120; 180}

\(BCNN\left(3;4;10\right)=30\)

Mà Bội số của 3;4;10 nhỏ hơn 200

\(\Rightarrow BC\left(3;4;10\right)=\left\{0;30;60;90;120;150;180\right\}\)

                             Để olm giúp em nha. 

Vì xóa chữ số 4 đi thì được số bé nên số lớn gấp 10 lần số bé và 4 đơn vị

Ta có sơ đồ: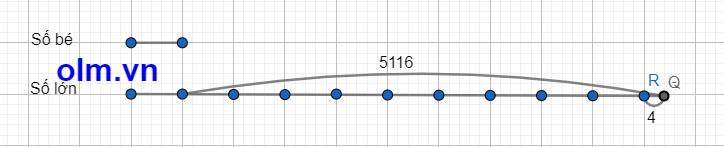 

Theo sơ đồ ta có: Số bé là: 

  (5116 - 4): (10 - 1) = 568 

Số lớn là: 5116 + 568 = 5684

Đáp số: số bé 568

             số lớn là 5684 

Ta có: l x+1l lớn hơn hoặc bằng 0, với mọi x

          l 2y -3l lớn hơn hoặc bằng 0, với mọi y

=> l x+1l + l 2y-3l lớn hơn hoặc bằng 0, với mọi x,y

=> l x+1l + l 2y-3l + 5 lớn hơn hoặc bằng 5

=> 1/ lx+1l + l2y-3l + 5 bé hơn hoặc bằng 1/5

=> 20/ lx+1l + l2y-3l+5 bé hơn hoặc bằng 20/5 = 4

Vậy max Q = 4

Dẫu "=" xảy ra <=> x = -1 ; y = 3/2

Chúc bạn học tốt!

Ta có: l x+1l lớn hơn hoặc bằng 0, với mọi x

          l 2y -3l lớn hơn hoặc bằng 0, với mọi y

=> l x+1l + l 2y-3l lớn hơn hoặc bằng 0, với mọi x,y

=> l x+1l + l 2y-3l + 5 lớn hơn hoặc bằng 5

=> 1/ lx+1l + l2y-3l + 5 bé hơn hoặc bằng 1/5

=> 20/ lx+1l + l2y-3l+5 bé hơn hoặc bằng 20/5 = 4

Vậy max Q = 4

Dẫu "=" xảy ra <=> x = -1 ; y = 3/2

\(\left(x+32\right)-17=52:4\)

\(\left(x+32\right)-17=13\)

\(\left(x+32\right)=13+17\)

\(x+32=30\)

\(x=30-32\)

\(x=-2\)

Vậy x=\(-2\)

(χ+32)-17 =52:4

(x+32)-17=13

(x+32)=13+17

x+32=30

x=30-32

x=−2

Vậy x=$-2$

Chiểu cao của hình thang ABCD là: 12 \(\times\) 2 : 3 = 8 (cm)

Tổng độ dài hai đáy của hình thang là: 100 \(\times\) 2 : 8 = 25(cm)

Ta có sơ đồ:

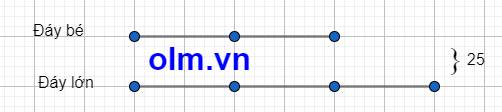
Theo sơ đồ ta có: Đáy bé: 25: ( 2+3) \(\times\) 2 = 10 (cm)

                              Đáy lớn là: 25 - 10 = 15 (cm)

                               Đáp số: Đáy bé 10 cm 

                                             Đáy lớn 15 cm 

\(\dfrac{5}{3}+\dfrac{7}{5}+\dfrac{20}{7}+\dfrac{19}{2}=\dfrac{5.3}{3.70}+\dfrac{7.42}{5.42}+\dfrac{20.30}{7.30}+\dfrac{19.105}{2.105}\)

\(=\dfrac{15}{210}+\dfrac{294}{210}+\dfrac{600}{210}+\dfrac{1995}{210}=\dfrac{2904}{210}=\dfrac{484}{35}\)

tính nhanh hay j

\(\dfrac{3}{2}.x-\dfrac{2}{7}.x< x-\dfrac{7}{2}\ge18\)

\(\Rightarrow\left\{{}\begin{matrix}x-\dfrac{7}{2}>\dfrac{3}{2}.x-\dfrac{2}{7}.x\\x-\dfrac{7}{2}\ge18\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}x-\dfrac{3}{2}.x+\dfrac{2}{7}.x>\dfrac{7}{2}\\x\ge18+\dfrac{7}{2}\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}\left(1-\dfrac{3}{2}+\dfrac{2}{7}\right).x>\dfrac{7}{2}\\x\ge\dfrac{36}{2}+\dfrac{7}{2}\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}\left(\dfrac{14}{14}-\dfrac{21}{14}+\dfrac{4}{14}\right).x>\dfrac{7}{2}\\x\ge\dfrac{43}{2}\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}\left(-\dfrac{3}{14}\right).x>\dfrac{7}{2}\\x\ge\dfrac{43}{2}\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}x< \dfrac{7}{2}:\left(-\dfrac{3}{14}\right)\\x\ge\dfrac{43}{2}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x< \dfrac{7}{2}.\left(-\dfrac{14}{3}\right)\\x\ge\dfrac{43}{2}\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}x< -\dfrac{49}{3}\\x\ge\dfrac{43}{2}\end{matrix}\right.\) \(\Rightarrow x\in\varnothing\)

Bài toán này kiến thức vượt lớp 5 (dấu . là dấu nhân)

giiups tui nhanh nhanh

315+[125-x]=435

125-x=435-315

125-x=120

x=125-120

x=5 

\(315+\left(125-x\right)=435\)

\(125-x=435-315\)

\(125-x=120\)

\(x=125-120\)

\(x=5\)

a) Ta có: x²\(\ge0,\forall x\) 

=> x² +3/4 \(\ge\dfrac{3}{4}\) , mọi x

Vậy min A = 3/4

Dấu "=" xảy ra <=> x =0

b) ( x- 3/2)² -0,4

Ta có ( x-3/2)² lớn hơn hoặc bằng 0, mọi x

=> ( x-3/2)² - 0,4 lớn hơn hoặc bằng 0 - 0;4 = -0,4

Vậy min B =-0,4

Dấu "=" xảy ra <=> x = 3/2

Chúc bạn học tốt !

bạn cho mik hỏi là min A nghĩa là sao vậy