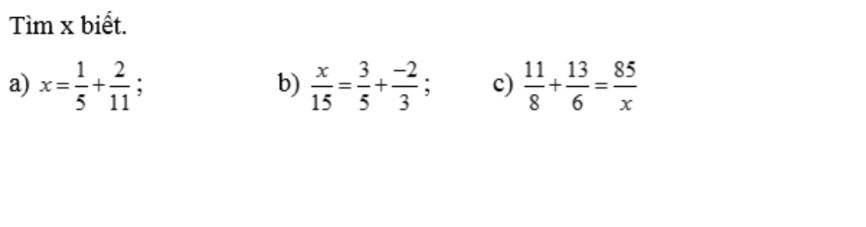
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đặt :
�
=
2
1
⋅
3
+
2
3
⋅
5
+
2
5
⋅
7
+
.
.
.
+
2
99
⋅
101
A=
1⋅3
2
+
3⋅5
2
+
5⋅7
2
+...+
99⋅101
2
�
−
2
1
⋅
3
=
2
3
⋅
5
+
2
5
⋅
7
+
.
.
.
+
2
99
⋅
101
A−
1⋅3
2
=
3⋅5
2
+
5⋅7
2
+...+
99⋅101
2
2
�
−
2
1
⋅
3
=
2
3
−
2
5
+
2
5
−
2
7
+
2
7
−
.
.
.
+
2
99
−
2
101
2A−
1⋅3
2
=
3
2
−
5
2
+
5
2
−
7
2
+
7
2
−...+
99
2
−
101
2
2
�
−
2
3
=
2
3
−
2
101
2A−
3
2
=
Đặt :
�
=
2
1
⋅
3
+
2
3
⋅
5
+
2
5
⋅
7
+
.
.
.
+
2
99
⋅
101
A=
1⋅3
2
+
3⋅5
2
+
5⋅7
2
+...+
99⋅101
2
�
−
2
1
⋅
3
=
2
3
⋅
5
+
2
5
⋅
7
+
.
.
.
+
2
99
⋅
101
A−
1⋅3
2
=
3⋅5
2
+
5⋅7
2
+...+
99⋅101
2
2
�
−
2
1
⋅
3
=
2
3
−
2
5
+
2
5
−
2
7
+
2
7
−
.
.
.
+
2
99
−
2
101
2A−
1⋅3
2
=
3
2
−
5
2
+
5
2
−
7
2
+
7
2
−...+
99
2
−
101
2
2
�
−
2
3
=
2
3
−
2
101
2A−
3
2
=
3
2
−
101
2
2
�
−
2
3
=
196
303
2A−
3
2
=
303
196
�
−
2
3
=
98
303
A−
3
2
=
303
98
�
=
98
303
+
2
3
=
100
101
A=
303
98
+
3
2
=
101
100
3
2
−
101
2
2
�
−
2
3
=
196
303
2A−
3
2
=
303
196
�
−
2
3
=
98
303
A−
3
2
=
303
98
�
=
98
303
+
2
3
=
100
101
A=
303
98
+
3
2
=
101
100

\(C=\dfrac{5}{3-\left(4x+1\right)^2}\)
Điều kiện xác định khi
\(3-\left(4x+1\right)^2\ne0\Leftrightarrow\left[{}\begin{matrix}4x+1\ne\sqrt[]{3}\\4x+1\ne-\sqrt[]{3}\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x\ne\dfrac{\sqrt[]{3}-1}{4}\\x\ne\dfrac{-\sqrt[]{3}-1}{4}\end{matrix}\right.\)
Ta có :
\(\left(4x+1\right)^2\ge0,\forall x\)
\(\Leftrightarrow3-\left(4x+1\right)^2\le3\)
\(\Leftrightarrow C=\dfrac{5}{3-\left(4x+1\right)^2}\ge\dfrac{5}{3}\)
Vậy \(GTNN\left(C\right)=\dfrac{5}{3}\left(tạix=-\dfrac{1}{4}\right)\)
\(B=\left(2x\right)^2+2\left(y-1\right)^2-5\)
vì \(\left\{{}\begin{matrix}\left(2x\right)^2\ge0,\forall x\\2\left(y-1\right)^2\ge0,\forall y\end{matrix}\right.\)
\(\Rightarrow B=\left(2x\right)^2+2\left(y-1\right)^2-5\ge-5\)
Dấu "=" xảy tại khi
\(\left\{{}\begin{matrix}2x=0\\2\left(y-1\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=1\end{matrix}\right.\)
Vậy \(GTNN\left(B\right)=-5\left(tạix=0;y=1\right)\)

a, ( \(\dfrac{1}{4}\) + \(\dfrac{-5}{13}\)) +( \(\dfrac{2}{11}\) + \(\dfrac{-8}{13}\) + \(\dfrac{3}{4}\))
= \(\dfrac{1}{4}\) - \(\dfrac{5}{13}\) + \(\dfrac{2}{11}\) - \(\dfrac{8}{13}\) + \(\dfrac{3}{4}\)
= ( \(\dfrac{1}{4}\) + \(\dfrac{3}{4}\)) - ( \(\dfrac{5}{13}\) + \(\dfrac{8}{13}\)) + \(\dfrac{2}{11}\)
= 1 - 1 + \(\dfrac{2}{11}\)
= \(\dfrac{2}{11}\)
b, ( \(\dfrac{21}{31}\) + \(\dfrac{-16}{7}\)) +( \(\dfrac{44}{53}\) + \(\dfrac{10}{31}\)) + \(\dfrac{9}{53}\)
= \(\dfrac{21}{31}-\dfrac{16}{7}+\dfrac{44}{53}+\dfrac{10}{31}+\dfrac{9}{53}\)
= ( \(\dfrac{21}{31}\) + \(\dfrac{10}{31}\)) + ( \(\dfrac{44}{53}\) + \(\dfrac{9}{53}\)) - \(\dfrac{16}{7}\)
= 1 + 1 - \(\dfrac{16}{7}\)
= \(\dfrac{14}{7}-\dfrac{16}{7}\)
= - \(\dfrac{2}{7}\)

\(\text{#040911}\)
Vì \(-\dfrac{5}{12}< 0\)
\(\Rightarrow-\dfrac{5}{12}< \dfrac{a}{5}\text{ }\forall\text{ }a\)
\(\dfrac{a}{5}< \dfrac{1}{4}\)
\(\Rightarrow a=1\)
Vậy, để thỏa mãn \(-\dfrac{5}{12}< \dfrac{a}{5}< \dfrac{1}{4}\) thì \(a=1.\)

B = [1200 - ( 16 - 6 )3 ] : 40
B = [1200 - 103 ] : 40
B = [1200 - 1000] : 40
B = 200 : 40
B = 5
B = [ 1200 - (42 - 2.3)3 ] : 40
B = [ 1200 - (16 - 6)3 ] : 40
B = [ 1200 - 1000]: 40
B = 200: 40
B = 5

\(\left(1-\dfrac{1}{2}\right)\times\left(1-\dfrac{1}{3}\right)\times\left(1-\dfrac{1}{4}\right)\times...\times\left(1-\dfrac{1}{2023}\right)\\ =\dfrac{1}{2}\times\dfrac{2}{3}\times\dfrac{3}{4}\times...\times\dfrac{2022}{2023}\\ =\dfrac{1}{2023}\)


Bài 4:
b. Ta có:
$(2-x)^2\geq 0$ với mọi $x$
$(y-1)^2\geq 0$ với mọi $y$
$\Rightarrow B=(2-x)^2+2(y-1)^2-5\geq 0+2.0-5=-5$
Vậy $B_{\min}=-5$. Giá trị này đạt tại $2-x=y-1=0$
$\Lefrightarrow x=2; y=1$
c.
Ta thấy: $(4x+1)^2\geq 0$ với mọi $x$
$\Rightarrow 3-(4x+1)^2\leq 3$
$\Rightarrow C=\frac{5}{3-(4x+1)^2}\geq \frac{5}{3}$
Vậy $C_{\min}=\frac{5}{3}$. Giá trị này đạt tại $4x+1=0\Leftrightarrow x=\frac{-1}{4}$
Bài 5:
c.
Vì:
$(2x+1)^2\geq 0$ với mọi $x$
$(y-3,5)^2\geq 0$ với mọi $y$
$\Rightarrow -P= (2x+1)^2+7(y-3,5)^2-\frac{2}{3}\geq 0+7.0-\frac{2}{3}=\frac{-2}{3}$
$\Rightarrow P\leq \frac{2}{3}$
Vậy $P_{\max}=\frac{2}{3}$. Giá trị này đạt tại $2x+1=y-3,5=0$
$\Leftrightarrow x=\frac{-1}{2}; y=3,5$
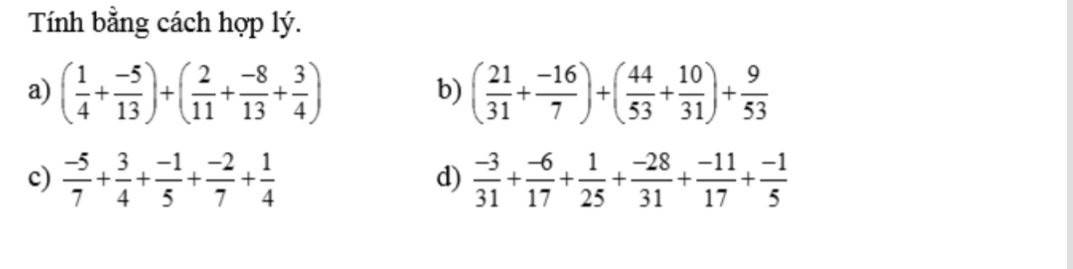

a) x = \(\dfrac{1}{5}+\dfrac{2}{11}\)
x = \(\dfrac{11}{55}\) + \(\dfrac{10}{55}\)
x = \(\dfrac{21}{55}\)
b) \(\dfrac{x}{15}\) = \(\dfrac{3}{5}+\dfrac{-2}{3}\)
\(\dfrac{x}{15}=\dfrac{9}{15}+\dfrac{-10}{15}\)
\(\dfrac{x}{15}=\dfrac{-1}{15}\)
\(x=\dfrac{-1}{15}\cdot15\)
x = -1
c) \(\dfrac{11}{8}+\dfrac{13}{6}=\dfrac{85}{x}\)
\(\dfrac{33}{24}+\dfrac{52}{24}=\dfrac{85}{x}\)
\(\dfrac{85}{24}=\dfrac{85}{x}\)
\(\dfrac{85}{x}=\dfrac{85}{24}\)
\(x=85:\dfrac{85}{24}\)
\(x=85\cdot\dfrac{24}{85}\)
\(x=24\)