`@` `\text {Ans}`

`\downarrow`

`2.x + 25 + 3.x = 50`

`\Rightarrow x.(2 + 3) = 50 - 25`

`\Rightarrow 5x = 25`

`\Rightarrow x = 25 \div 5`

`\Rightarrow x = 5`

Vậy, `x = 5.`

`@` `\text {Ans}`

`\downarrow`

`h)`

\(\left(\dfrac{7}{111}-\dfrac{4}{33}+\dfrac{9}{37}\right)\cdot\left(\dfrac{1}{2}-\dfrac{1}{3}-\dfrac{1}{6}\right)\)

`=`\(\left(\dfrac{7}{111}-\dfrac{4}{33}+\dfrac{9}{37}\right)\cdot\left(\dfrac{3}{6}-\dfrac{2}{6}-\dfrac{1}{6}\right)\)

`=`\(\left(\dfrac{7}{111}-\dfrac{4}{33}+\dfrac{9}{37}\right)\cdot\left(\dfrac{3-2-1}{6}\right)\)

`=`\(\left(\dfrac{7}{111}-\dfrac{4}{33}+\dfrac{9}{37}\right)\cdot0=0\)

a) 2x + 1 = 3

2x = 2

x = 1

b) ( 2x - 5 ) + 17 = 6

( 2x - 5 ) = 6 - 17

( 2x - 5 ) = -11

2x = -11 + 5

2x = -6

x = -3

c) 10 - 2 x ( 4 - 3x ) = -4

2 x ( 4 - 3x ) = 14

4 - 3x = 7

3x = -3 

x = -1 

a) 2x + 1 = 3

2x = 3-1

2x=2

x=2:2

x=1

Ý tưởng; Dựa vào "thế hình" của đề bài, ta dự đoán biểu thức trong căn sẽ phân tích được thành lũy thừa bậc 3 của một biểu thức có dạng \(a+\sqrt{3}\left(a\inℤ\right)\). Ta thấy:

 \(\left(a+\sqrt{3}\right)^3=a^3+3a^2\sqrt{3}+9a+3\sqrt{3}\) \(=a^3+9a+\left(3a^2+3\right)\sqrt{3}\)

 Ta có hệ: \(\left\{{}\begin{matrix}a^3+9a=26\\3a^2+3=15\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a\left(a^2+9\right)=26\\a^2+1=5\end{matrix}\right.\)

\(\Rightarrow a=\pm2\). Nhưng rõ ràng \(a=-2\) không thỏa. Vậy \(a=2\).

 Trình bày: Ta có

 \(\sqrt[3]{26+15\sqrt{3}}\)

\(=\sqrt[3]{8+12\sqrt{3}+18+3\sqrt{3}}\)

\(=\sqrt[3]{2^3+3.2^2.\sqrt{3}+3.2\left(\sqrt{3}\right)^2+\left(\sqrt{3}\right)^3}\)

\(=\sqrt[3]{\left(2+\sqrt{3}\right)^3}\)

\(=2+\sqrt{3}\)

`-` Góc đối đỉnh với \(\widehat{mOx}\) trong hình bên là \(\widehat{nOy}\)

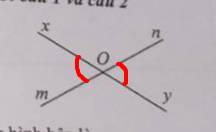
`\Rightarrow B`

`-` Các góc kề bù với \(\widehat{xOm}\) trong hình bên là \(\widehat{xOn}\text{ và }\widehat{mOy}\) 

`\Rightarrow C.`

Help me, có ai bt đáp án và giải thik cho mik vs 

\(...=1+1+...+1+1\)

Số số 1 là :

\(\left(2022-2\right):2+1+1=1012\left(số\right)\)

Vậy kết quả là \(1x1012=1012\)

Số số 1 là :

$\left(2022-2\right):2+1+1=1012\left(số\acute{\hat{o}}\right)$

Vậy kết quả là $1x1012=1012$

\(A=n.n+n+1\)

\(\Rightarrow A=n.\left(n+1\right)+1\)

mà \(n.\left(n+1\right)⋮2\)

Nên \(n.\left(n+1\right)+1\) không chia hết cho 5

\(\Rightarrow dpcm\)

a, 72 = 2³.3²;    24 = 2³.3 

ƯCLN(72; 24) = 2³.3 = 24

ƯC(72; 24) = { 1; 2; 3; 4; 6; 8; 12; 24}

b, 30; 60; 20

 30 = 2.3.5;                 60 = 2².3.5;                 20 = 2.5

 ƯCLN(30; 60; 20) = 2.5 = 10

ƯC(30; 60; 20) = { 1; 2; 5; 10}