`@` `\text {Ans}`

`\downarrow`

`2,`

`a)`

`-5x^2y^4z^5 (-3xyz^2)`

`= (-5).(-3) . (x^2 . x) . (y^4 . y) . (z^5 . z^2)`

`= 15 x^3 y^5 z^7`

Hệ số: `15`

Phần biến: `x^3 y^5 z^7`

Bậc: `3 + 5 + 7 = 15`

`b)`

`12xy^3z^5 .`\((\dfrac{1}{4}x^3z^3)\)

`=`\((12. \dfrac{1}{4})\)`. (x . x^3) . y^3 . (z^5 . z^3)`

`= 3 x^4 y^3 z^8`

Hệ số: `3`

Phần biến: `x^4y^3z^8`

Bậc: `4+3+8 = 15`

`c)`

\(x^3 . (\dfrac{-5}{4}x^2y)(\dfrac{2}{5}x^3y^4)\)

`=`\(\left(-\dfrac{5}{4}\cdot\dfrac{2}{5}\right)\left(x^3\cdot x^2\cdot x^3\right)\left(y\cdot y^4\right)\)

`=`\(-\dfrac{1}{2}x^8y^5\)

Hệ số: \(-\dfrac{1}{2}\)

Phần biến: `x^8y^5`

Bậc: `8 + 5 = 13`

Ta có \(2\sin x\cos x=\left(\sin x+\cos x\right)^2-\left(\sin^2x+\cos^2x\right)\) 

\(=\left(\dfrac{3}{4}\right)^2-1=-\dfrac{7}{16}\)  

Từ đó \(A=\left|\sin x-\cos x\right|\)

\(\Rightarrow A^2=\left(\sin x-\cos x\right)^2\)

\(A^2=\sin^2x+\cos^2x-2\sin x\cos x\)

\(A^2=1+\dfrac{7}{16}=\dfrac{23}{16}\)

\(\Rightarrow A=\dfrac{\sqrt{23}}{4}\) (do \(A\ge0\))

Có \(\cos x+\sin x=\dfrac{3}{4}\)

\(\Leftrightarrow\left(\cos x+\sin x\right)^2=\dfrac{9}{16}\)

\(\Leftrightarrow2.\sin x.\cos x+1=\dfrac{9}{16}\)

\(\Leftrightarrow\sin x.\cos x=-\dfrac{7}{32}\)

Lại có \(\left(\cos x+\sin x\right)^2=\left(\cos x-\sin x\right)^2+4.\sin x.\cos x=\dfrac{9}{16}\)

\(\Leftrightarrow\left(\cos x-\sin x\right)^2=\dfrac{23}{16}\)

\(\Leftrightarrow\left|\sin x-\cos x\right|=\dfrac{\sqrt{23}}{4}\)

 Đối với điểm A nằm ngoài đường tròn (O;R), kí hiệu d_A là đường thẳng nối 2 tiếp điểm của 2 tiếp tuyến kẻ từ A tới (O).

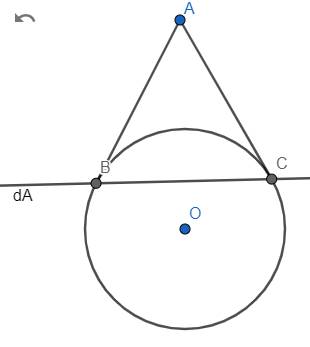
 Đối với điểm A nằm bên trong đường tròn, kí hiệu d_A để chỉ đường thẳng vuông góc với OA tại T với T là điểm mà \(OA.OT=R^2\) và A nằm giữa O và T.

Để giải được bài toán này, ta cần xét tính chất sau của đường d_A:

 TC1: \(A\in d_B\Leftrightarrow B\in d_A\), tính chất này là hiển nhiên theo định nghĩa đường d_A.

 TC2: A, B, C thẳng hàng khi và chỉ khi d_A, d_B, d_C đồng quy hoặc đôi một song song.

CM: Nếu \(O\in AB\) thì hiển nhiên TC2 đúng.

Nếu \(O\notin AB\) thì gọi P là giao điểm của d_A, d_B. Vì \(P\in d_A,P\in d_B\) nên theo TC1, \(A\in d_P,B\in d_P\) nên \(AB\equiv d_P\). Do đó A, B, C thẳng hàng khi và chỉ khi \(C\in d_P\), có nghĩa là \(P\in d_C\) hay d_A, d_B, d_C đồng quy tại P, TC2 được chứng minh.

 Bây giờ ta sẽ xét bổ đề sau:

 Bổ đề: Cho tam giác ABC, I là tâm đường tròn nội tiếp. K là trực tâm của tam giác IBC. M, N lần lượt là trung điểm của AB, AC. Khi đó \(MN\equiv d_K\) (đối với đường tròn I)

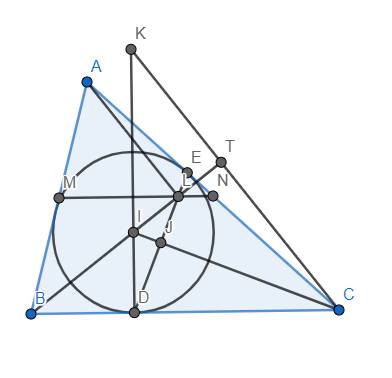
 CM: Gọi D, E lần lượt là tiếp điểm của (I) với BC, CA. DE cắt BI, CI, KC lần lượt tại L, J, T. Theo tính chất quen thuộc thì \(\widehat{BLA}=90^o\), suy ra \(ML=MA=MB\). Từ đó \(\widehat{MLB}=\widehat{MBL}=\widehat{LBC}\), suy ra ML//BC hay \(L\in MN\). 

 Mặt khác, vì \(\widehat{LTC}=\widehat{LJC}=90^o\) nên tứ giác CJLT nội tiếp \(\Rightarrow IL.IT=IJ.IC=r^2\) (\(r\) là bán kính đường tròn (I)), theo định nghĩa đường \(d_X\) , suy ra được \(KC\equiv d_L\). Từ đó suy ra \(K\in d_L\). Theo TC1 suy ra \(L\in d_K\). Mà \(L\in MN,MN\perp IK\) nên theo định nghĩa đường \(d_X\), suy ra \(MN\equiv d_K\). Vậy bổ đề được chứng minh.

 Bây giờ ta sẽ quay lại bài toán chính:

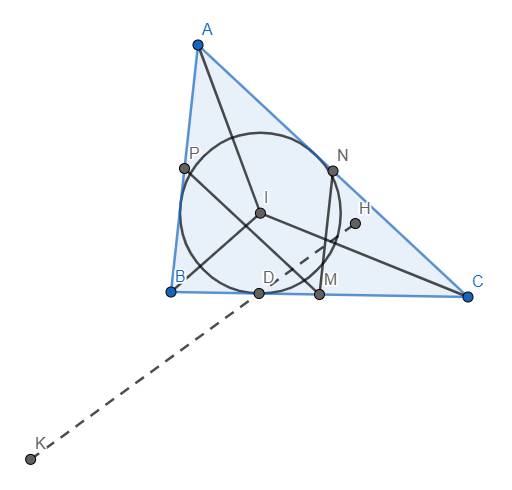
 Từ kết quả của bổ đề, ta suy ra \(MN\equiv d_K,MP\equiv d_H\)

 Mặt khác, theo định nghĩa, ta có \(DM\equiv d_D\).

 Để ý rằng MN, MP, MD đồng quy tại M nên theo TC2, suy ra H, K, I thẳng hàng. Suy ra đpcm.

 Ở chỗ cuối phải là \(MN\equiv d_H,MP\equiv d_K\) chứ không phải ngược lại đâu. (bổ sung thêm M, N, P lần lượt là trung điểm của BC, CA, AB)

Có nhìu cách, tham khảo nha (mình có 2 cách, bạn chọn cách nào cũng ok):

 Gọi số cần tìm là x
Theo bài ra ta có
x = 7a + 5 va x= 13b + 4
Ta lại có x + 9 = 7a + 14 = 13b + 13
-> x + 9 chia hết cho 7 và 13
-> x + 9 chia hết cho 7.13 = 91
-> x + 9 = 91m -> x = 91m - 9 = 91(m -1 + 1) - 9 = 91(m-1) + 82
Vậy x chia 91 dư 82

câu trả lời 2:

a = 7x + 5 = 13y + 11

Mà a + 2 = 7k + 7 = 13k + 13

=> a + 2 chia hết cho 7 và 13

=> a + 2 chia hết cho 7.13 = 91

=> a + 2 = 91z

=> a = 91z - 2 = 91.(z + 1 - 1) - 2 = 91.(z - 1) + 89

Vậy a chia 91 dư 89.

Ai tick cho mình với!!!!!!!!!!!!

        THAM KHẢO NHÉ. XIN LỖI VÌ KO TRÙNG ĐỀ

Giải thích các bước giải:

a.Gọi $K$ là tâm đường tròn bàng tiếp trong góc $A$ 

$\to BK,CK$ lần lượt là phân giác ngoài tại đỉnh $B,C$

 Ta có $\left(K\right)$ tiếp xúc $AB,AC$ lần lượt tại $E,F$

$\to AF,AE$ là tiếp tuyến của $\left(K\right)$

$\to AF=AE$

b.Vì $\left(K\right)$ tiếp xúc với $BC$ tại $D\to BC$ là tiếp tuyến của $\left(K\right)$

Ta có $BD,BE$ là tiếp tuyến của $\left(K\right)\to BD=BE$

           $CD,CF$ là tiếp tuyến của $\left(K\right)\to CD=CF$

c.Ta có: 

$AE+AF=(AB+BE)+(AC+CF)=AB+AC+(BE+CF)=AB+AC+(BD+DC)=AB+AC+BC=P_{AB}$

okay :vvv

(a+b) x c = ac + bc

a + b x c = ( a x c) + ( b x c)

chúc bạn học giỏi nha

a) \(A=\left\{\overline{abc};\overline{acb};\overline{bac};\overline{bca};\overline{cab};\overline{cba}\right\}\)

b) Hai số nhỏ nhất là \(\overline{abc};\overline{acb}\)

Theo đề bài ta có :

\(\overline{abc}+\overline{acb}=488\)

\(\Rightarrow100a+10b+c+100a+10c+b=488\)

\(\Rightarrow200+10b+10c+\left(b+c\right)=488\)

\(\Rightarrow200a+10\left(b+c\right)+\left(b+c\right)=400+8.10+8\)

\(\Rightarrow\left\{{}\begin{matrix}a=400:200=2\\b+c=8\end{matrix}\right.\)

mà \(0< a< b< c\)

\(\Rightarrow\left\{{}\begin{matrix}a=2\\b=3\\c=5\end{matrix}\right.\)

Vậy 3 chữ số đó là 2 ;3; 5

Mik vẽ hình không được đẹp lắm nên thông cảm  nha