Bậc của đa thức \(P = 3 x^{2} - 3 x^{4} + \frac{1}{2} x^{5} + 0 , 75\) là
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Xác suất của sự kiện lấy được quả bóng màu đỏ là:
15 : 50 = \(\frac{3}{10}\)

Giải:
Theo bài ra ta có:
\(\overline{ba}\) = 2 x \(\overline{ab}\) + 18
10b + a = 20a + 2b + 18
10b - 2b = 20a - a + 18
8b = 19a + 8
8b + 19b = 19b + 19a + 8
27b = 19.(a + b) + 18 (1)
Thay a + b = 9 vào (1)
27b = 19.9 + 18
27b = 171 + 18
27b = 189
b = 189 : 27
b = 7
a = 9 - b
a = 9 - 7
a = 2
Vậy \(\overline{ab}\) = 27

Bài này kết quả -11 đúng không cả nhà ơi
= 2(-1) - 5.1 + 4.-1 -3 = -11
Khi x=-1 thì \(P\left(-1\right)=2\cdot\left(-1\right)^3-5\cdot\left(-1\right)^2+4\cdot\left(-1\right)-3\)
\(=2\cdot\left(-1\right)-5\cdot1-4-3\)
=-2-5-4-3
=-7-3-4
=-14

9,15 : 0,5 + 9,15 x 9 - 9,15
= 9,15 x 2 + 9,15 x 9 - 9,15 x 1
= 9,15 x (2 + 9 - 1)
= 9,15 x (11 - 1)
= 9,15 x 10
91,5

Giải:
Thời gian ô tô thứ nhất đi từ A đến B không kể thời gian nghỉ là:
10 giờ 30 phút - 30 phút - 6 giờ = 4 giờ
Cùng một quãng đường vận tốc tỉ lệ nghịch với thời gian nên tỉ số thời gian xe thứ nhất và thời gian xe thứ hai đi hết quãng đường AB là:
40 : 45 = \(\frac89\)
Thời gian xe thứ hai đi hết quãng đường AB không kể thời gian nghỉ là:
4 : \(\frac89\) = 4,5 (giờ)
Ô tô thứ hai đến B lúc:
6 giờ + 4,5 giờ + 30 phút = 11 giờ
Đáp số: 11 giờ

Ta có: \(\left(3x-\dfrac{1}{6}\right)^2>=0\forall x\)
\(\left|2y-6\right|>=0\forall y\)
Do đó: \(\left(3x-\dfrac{1}{6}\right)^2+\left|2y-6\right|>=0\forall x,y\)
mà \(\left(3x-\dfrac{1}{6}\right)^2+\left|2y-6\right|< =0\)
nên \(\left\{{}\begin{matrix}3x-\dfrac{1}{6}=0\\2y-6=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x=\dfrac{1}{6}\\2y=6\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{1}{18}\\y=3\end{matrix}\right.\)

\(x^2+2,5x+5\)
\(=x^2+2\cdot x\cdot\dfrac{5}{4}+\dfrac{25}{16}+\dfrac{55}{16}\)
\(=\left(x+\dfrac{5}{4}\right)^2+\dfrac{55}{16}>=\dfrac{55}{16}>0\forall x\)
=>ĐPCM
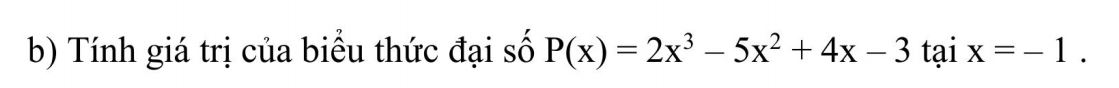
`P=3x^2-3x^4+1/2x^5+0,75`
`=1/2x^5-3x^4+3x^2+0,75`
Bậc của B chính là bậc của hạng tử có bậc cao nhất là `1/2x^5` có bậc 5
`=>P` có bậc 5`