Bác Năm nuôi cả gà và vịt tổng cộng 145 con. Bác Năm đã bán hết 13 con gà và 22 con vịt nên còn lại số gà bằng 2/3 số vịt. Hỏi lúc chưa bán, Bác Năm có bao nhiêu con gà, bao nhiêu con vịt?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, \(sin^2x+cos^2x=1\Leftrightarrow cos^2x=1-\dfrac{9}{25}=\dfrac{16}{25}\Leftrightarrow cosx=\dfrac{4}{5}\)
\(tanx=\dfrac{sinx}{cosx}=-\dfrac{3}{5}:\left(\dfrac{4}{5}\right)=-\dfrac{3}{4}\)
\(cotx=-\dfrac{4}{3}\)
c, \(sin^2x+cos^2x=1\Leftrightarrow sin^2x=1-\dfrac{9}{25}=\dfrac{16}{25}\Leftrightarrow sinx=\dfrac{4}{5}\)
\(tanx=\dfrac{sinx}{cosx}=\dfrac{4}{5}:\dfrac{3}{5}=\dfrac{4}{3}\)
\(cotx=\dfrac{3}{4}\)
b, \(cos^2x+sin^2x=1\Leftrightarrow sin^2x=1-\dfrac{1}{16}=\dfrac{15}{16}\Leftrightarrow sinx=\dfrac{\sqrt{15}}{4}\)
\(tanx=\dfrac{\sqrt{15}}{4}:\dfrac{1}{4}=\sqrt{15}\)
\(cotx=\dfrac{1}{\sqrt{15}}\)
d, \(sin^2x+cos^2x=1\Leftrightarrow sin^2x=1-\dfrac{25}{169}=\dfrac{144}{169}\Leftrightarrow sinx=\dfrac{12}{13}\)
\(tanx=\dfrac{12}{13}:\left(-\dfrac{5}{13}\right)=-\dfrac{12}{5}\)
\(cotx=-\dfrac{5}{12}\)
a: \(\Omega< x< \dfrac{3}{2}\Omega\)
=>cosx<0
Ta có: \(sin^2x+cos^2x=1\)
=>\(cos^2x=1-sin^2x=1-\left(\dfrac{3}{5}\right)^2=\dfrac{16}{25}\)
mà cosx<0
nên \(cosx=-\dfrac{4}{5}\)
\(tanx=\dfrac{sinx}{cosx}=\dfrac{-3}{5}:\dfrac{-4}{5}=\dfrac{3}{4}\)
\(cotx=\dfrac{1}{tanx}=\dfrac{4}{3}\)
b: \(0< x< \dfrac{\Omega}{2}\)
=>sin x>0
\(sin^2x+cos^2x=1\)
=>\(sin^2x=1-\left(\dfrac{1}{4}\right)^2=\dfrac{15}{16}\)
mà sin x>0
nên \(sinx=\dfrac{\sqrt{15}}{4}\)
\(tanx=\dfrac{sinx}{cosx}=\dfrac{\sqrt{15}}{4}:\dfrac{1}{4}=\sqrt{15}\)
\(cotx=\dfrac{1}{tanx}=\dfrac{1}{\sqrt{15}}=\dfrac{\sqrt{15}}{15}\)
c: 0<x<90 độ
=>sin x>0
\(sin^2x+cos^2x=1\)
=>\(sin^2x=1-\left(\dfrac{3}{5}\right)^2=\dfrac{16}{25}=\left(\dfrac{4}{5}\right)^2\)
mà sin x>0
nên \(sinx=\dfrac{4}{5}\)
\(tanx=\dfrac{sinx}{cosx}=\dfrac{4}{5}:\dfrac{3}{5}=\dfrac{4}{3}\)
\(cotx=1:\dfrac{4}{3}=\dfrac{3}{4}\)
d: \(180^0< x< 270^0\)
=>sin x<0
\(sin^2x+cos^2x=1\)
=>\(sin^2x=1-\left(-\dfrac{5}{13}\right)^2=1-\dfrac{25}{169}=\dfrac{144}{169}\)
mà sin x<0
nên \(sinx=-\dfrac{12}{13}\)
\(tanx=\dfrac{sinx}{cosx}=\dfrac{-12}{13}:\dfrac{-5}{13}=\dfrac{12}{5}\)
\(cotx=\dfrac{1}{tanx}=\dfrac{5}{12}\)

a: Chiều cao từ đỉnh A xuống BC là:
15x40%=6(cm)
Diện tích tam giác ABC là:
\(S_{ABC}=\dfrac{1}{2}\cdot6\cdot15=45\left(cm^2\right)\)
b: \(AM=\dfrac{2}{3}AB\)
=>\(S_{AMC}=\dfrac{2}{3}\times S_{ABC}=30\left(cm^2\right)\)
Vì N là trung điểm của AC
nên \(S_{ANM}=\dfrac{1}{2}\times S_{ABC}=15\left(cm^2\right)\)
\(S_{ANM}+S_{BMNC}=S_{ABC}\)
=>\(15+S_{BMNC}=45\)
=>\(S_{BMNC}=30\left(cm^2\right)\)

a: Xét ΔABH vuông tại H và ΔCBA vuông tại A có
\(\widehat{ABH}\) chung
Do đó: ΔABH~ΔCBA
b: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
Xét ΔABC có BD là phân giác
nên \(\dfrac{AD}{AB}=\dfrac{CD}{BC}\)
=>\(\dfrac{AD}{6}=\dfrac{CD}{10}\)
=>\(\dfrac{AD}{3}=\dfrac{CD}{5}\)
mà AD+CD=AC=8cm
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AD}{3}=\dfrac{CD}{5}=\dfrac{AD+CD}{3+5}=\dfrac{8}{8}=1\)
=>\(AD=3\cdot1=3\left(cm\right);CD=5\cdot1=5\left(cm\right)\)
c:
ΔBAD vuông tại A
=>\(S_{BAD}=\dfrac{1}{2}\cdot BA\cdot AD=\dfrac{1}{2}\cdot6\cdot3=9\left(cm^2\right)\)
ΔBHA~ΔBAC
=>\(\dfrac{BH}{BA}=\dfrac{BA}{BC}=\dfrac{6}{10}=\dfrac{3}{5}\)
Xét ΔBAD vuông tại A và ΔBHI vuông tại H có
\(\widehat{ABD}=\widehat{HBI}\)
Do đó: ΔBAD~ΔBHI
=>\(\dfrac{S_{BAD}}{S_{BHI}}=\left(\dfrac{BA}{BH}\right)^2=\left(\dfrac{5}{3}\right)^2=\dfrac{25}{9}\)
=>\(S_{BHI}=S_{BAD}\cdot\dfrac{9}{25}=\dfrac{81}{25}\left(cm^2\right)\)

Tỉ số giữa số vải còn lại sau buổi sáng so với ban đầu là:
\(1-\dfrac{3}{11}=\dfrac{8}{11}\)
Tỉ số giữa số vải còn lại sau buổi chiều so với ban đầu là:
\(\dfrac{8}{11}\times\left(1-\dfrac{3}{8}\right)=\dfrac{8}{11}\times\dfrac{5}{8}=\dfrac{5}{11}\)
Độ dài tấm vải đó là:
\(16:\dfrac{5}{11}=16\times\dfrac{11}{5}=35,2\left(m\right)\)
Buổi sáng bán được:
\(35,2\times\dfrac{3}{11}=9,6\left(m\right)\)
Buổi chiều bán được:
35,2-9,6-16=9,6(m)
Số vải còn lại sau khi bán vào buổi sáng là:
\(1-\dfrac{3}{11}=\dfrac{8}{11}\) (tấm vải)
Số vải bán vào buổi chiều là:
\(\dfrac{8}{11}\times\dfrac{3}{8}=\dfrac{3}{11}\) (tấm vải)
Số vải còn lại sau khi bán vào buổi chiều là:
\(\dfrac{8}{11}-\dfrac{3}{11}=\dfrac{5}{11}\) (tấm vải)
Số mét vải ban đầu là:
\(16:\dfrac{5}{11}=35,2\) (m)
Số mét vải bán vào buổi sáng là:
\(35,2\times\dfrac{3}{11}=9,6\) (m)
Số mét vải bán vào buổi chiều là:
\(35,2\times\dfrac{3}{11}=9,6\) (m)
Đáp số:...

Gọi chữ số hàng chục là: a
Chữ số hàng đơn vị là: b
ĐK: \(a,b\in N,1\le a\le9;0\le b\le9\)
Ta có: b=4a (1)
Nếu thêm số 0 vào giữa 2 chữ số thì đc số hơn số cũ 180 nên ta có pt:
\(\overline{a0b}-\overline{ab}=180\Leftrightarrow100a+b-10a-b=180\Leftrightarrow90a=180\Leftrightarrow a=2\) (tm)
=> b=4*2=8 (tm)
Vậy số cần tìm là: 28

\(265,87\times63=16749,81\)
\(45,54:18=2,53\)
\(245,58+7,492=253,072\)
\(485,41-69,27=416,14\)

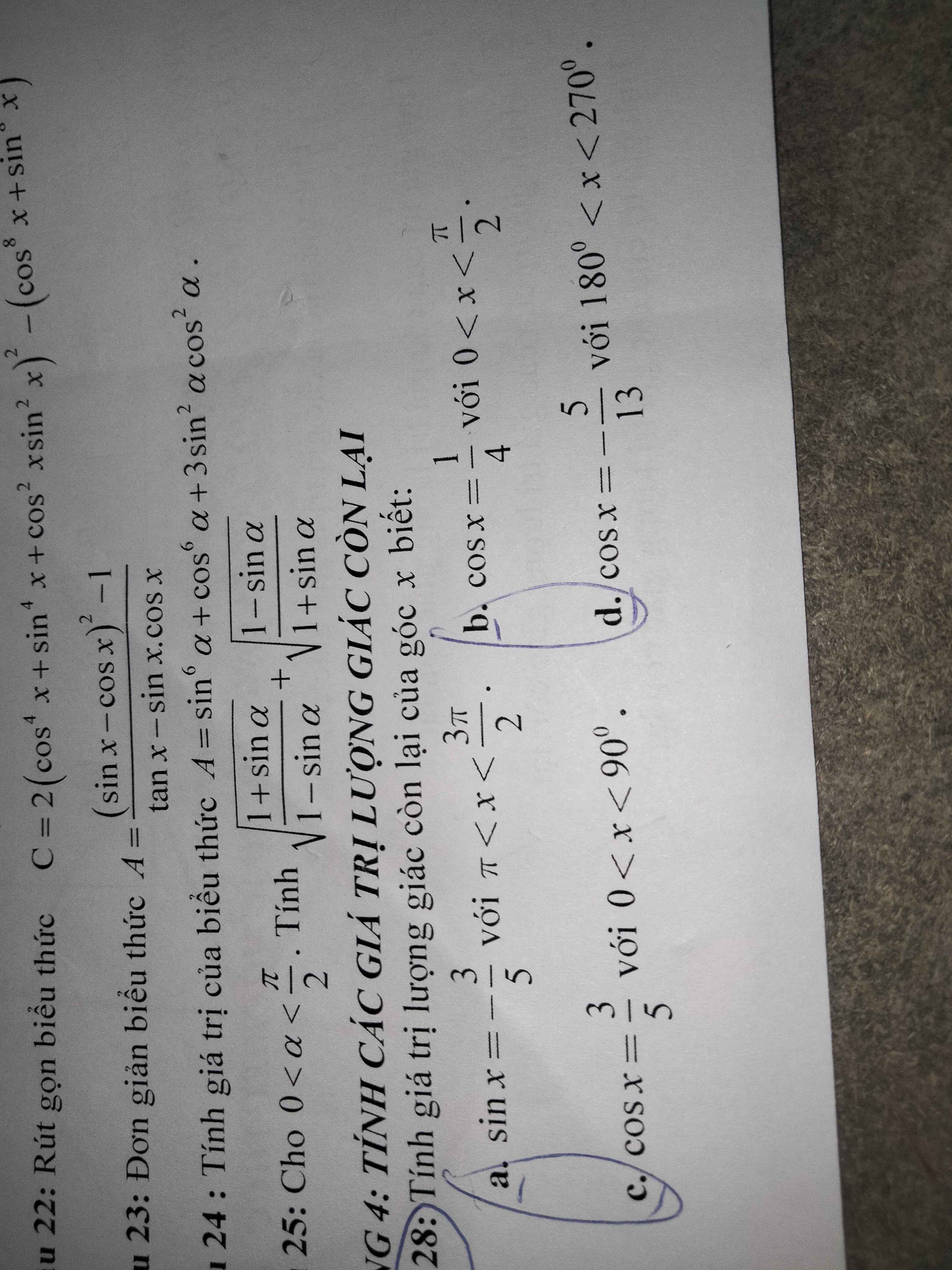

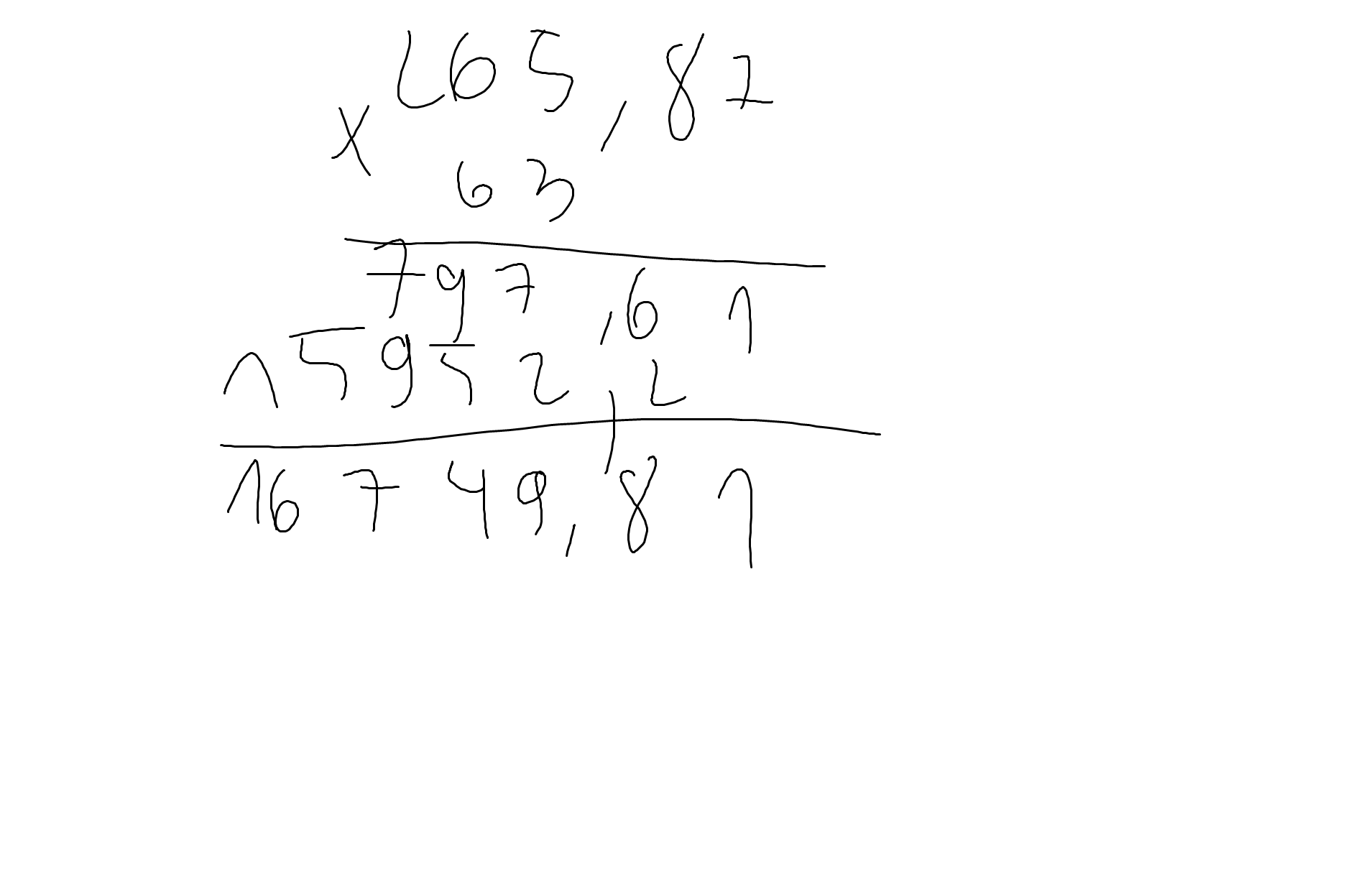
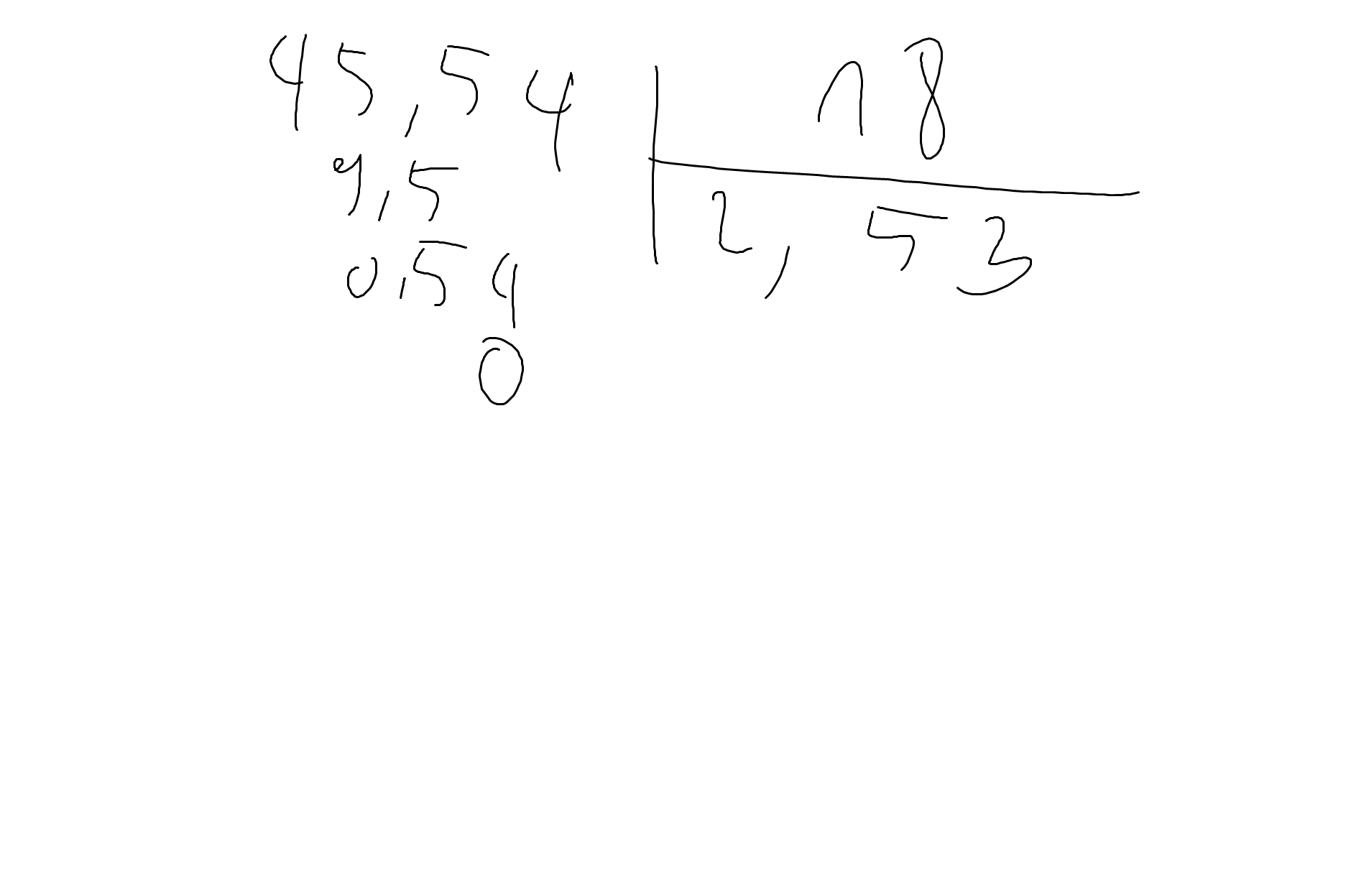

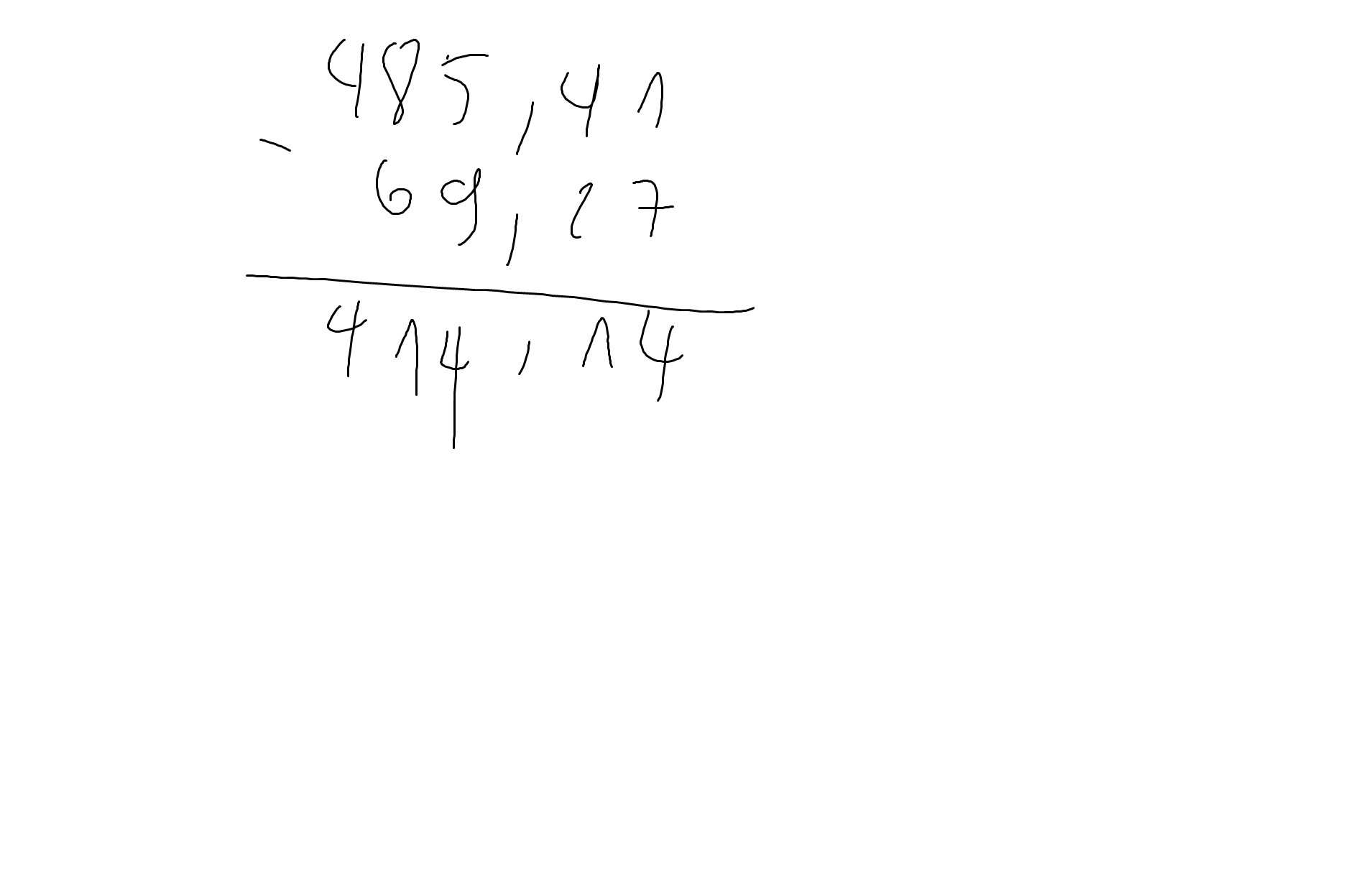
Tổng số gà vịt còn sau khi bán là:
145 - 13 - 22 = 110 (con)
Tổng số phần bằng nhau là:
2 + 3 = 5 (phần)
Số gà còn lại sau khi bán là:
110 : 5 x 2 = 44 (con)
Số gà ban đầu bác Năm có là:
44 + 13 = 57 (con)
Số vịt ban đầu là:
145 - 57 = 88 (con)
ĐS: ...
Tổng số gà vịt còn lại là:
145-13-22=110(con)
Số gà còn lại là \(110\times\dfrac{2}{3+2}=110\times\dfrac{2}{5}=44\left(con\right)\)
Số gà ban đầu là 44+13=57(con)
Số vịt ban đầu là 145-57=88(con)