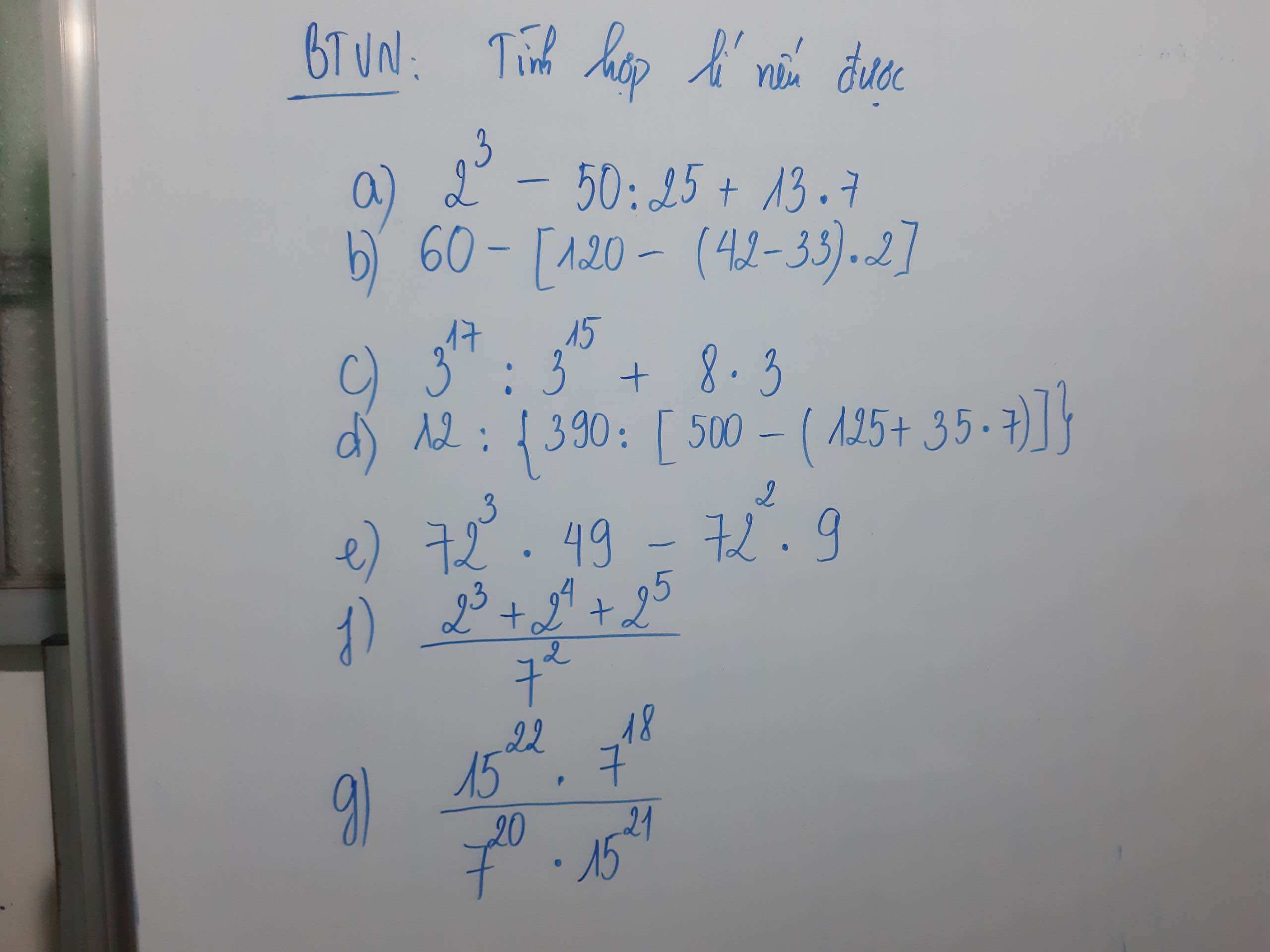 Làm chi tiết và viết rõ ra giúp mik nhé
Làm chi tiết và viết rõ ra giúp mik nhé
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


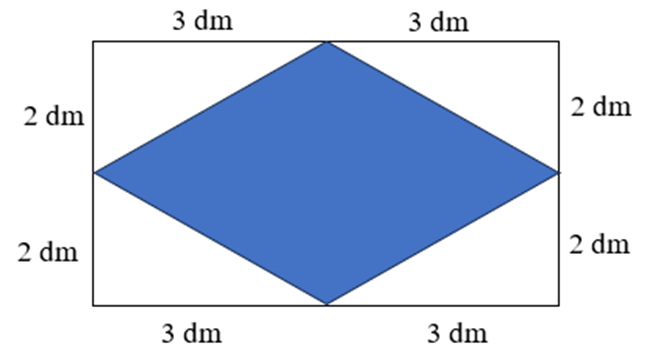
Diện tích của các hình là:
\(\left(2+2\right)\times\left(3+3\right)=24\left(dm^2\right)\)
Diện tích phần màu trắng là:
\(\dfrac{1}{2}\times2\times3+\dfrac{1}{2}\times2\times3+\dfrac{1}{2}\times2\times3+\dfrac{1}{2}\times2\times3=12\left(dm^2\right)\)
Diện tích phần tô màu là:
\(24-12=12\left(dm^2\right)\)
ĐS: ...

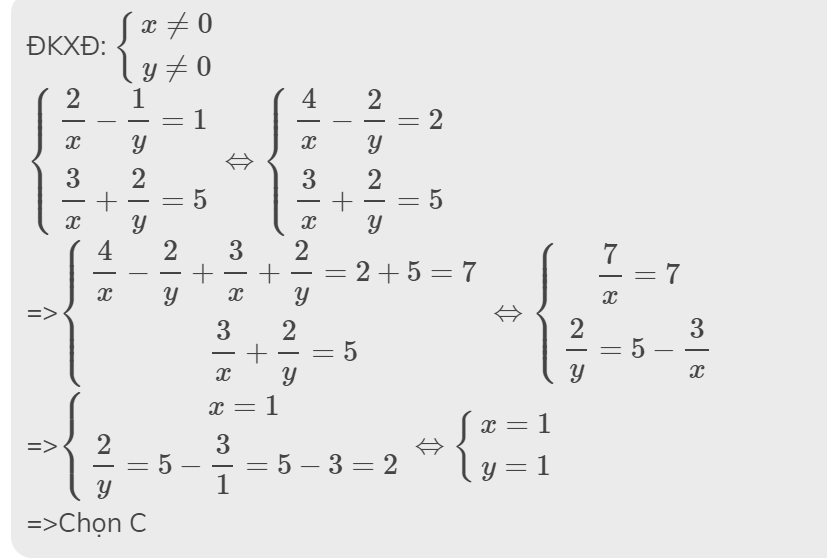
ĐKXĐ: \(\left\{{}\begin{matrix}x\ne0\\y\ne0\end{matrix}\right.\)
\(\left\{{}\begin{matrix}\dfrac{2}{x}-\dfrac{1}{y}=1\\\dfrac{3}{x}+\dfrac{2}{y}=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{4}{x}-\dfrac{2}{y}=2\\\dfrac{3}{x}+\dfrac{2}{y}=5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{4}{x}-\dfrac{2}{y}+\dfrac{3}{x}+\dfrac{2}{y}=2+5=7\\\dfrac{3}{x}+\dfrac{2}{y}=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{7}{x}=7\\\dfrac{2}{y}=5-\dfrac{3}{x}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=1\\\dfrac{2}{y}=5-\dfrac{3}{1}=5-3=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=1\end{matrix}\right.\)
=>Chọn C

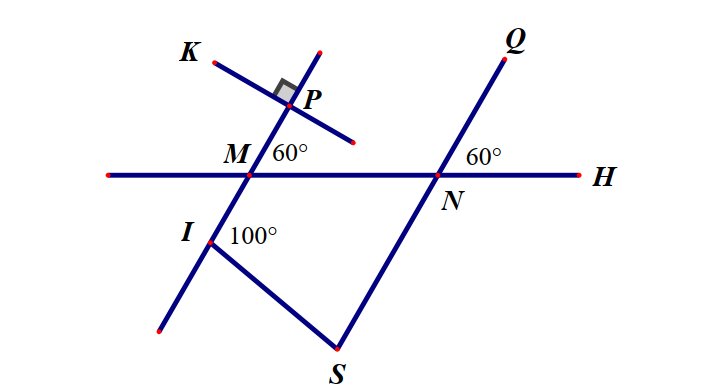
a: ta có: \(\widehat{MNS}=\widehat{HNQ}\)(hai góc đối đỉnh)
mà \(\widehat{HNQ}=60^0\)
nên \(\widehat{MNS}=60^0\)
b: Ta có: \(\widehat{QNH}=\widehat{PMN}\left(=60^0\right)\)
mà hai góc này là hai góc ở vị trí đồng vị
nên PI//QS
=>MP//NQ
c: ta có: MP//NQ
KP\(\perp\)MP
Do đó: KP\(\perp\)QN
d: ta có: MI//SN
=>\(\widehat{MIS}+\widehat{S}=180^0\)(hai góc trong cùng phía)
=>\(\widehat{S}+100^0=180^0\)
=>\(\widehat{S}=80^0\)

ĐKXĐ: \(\left\{{}\begin{matrix}x>=0\\y>=0\end{matrix}\right.\)
\(\left\{{}\begin{matrix}2\sqrt{x}+\sqrt{y}=5\\3\sqrt{x}-\sqrt{y}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2\sqrt{x}+\sqrt{y}+3\sqrt{x}-\sqrt{y}=5+1\\2\sqrt{x}+\sqrt{y}=5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}5\sqrt{x}=6\\\sqrt{y}=5-2\sqrt{x}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\sqrt{x}=\dfrac{6}{5}\\\sqrt{y}=5-2\cdot\dfrac{6}{5}=5-\dfrac{12}{5}=\dfrac{13}{5}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{36}{25}\\y=\dfrac{169}{25}\end{matrix}\right.\)
=>Chọn B
\(\left\{{}\begin{matrix}2\sqrt{x}+\sqrt{y}=5\\3\sqrt{x}-\sqrt{y}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5\sqrt{x}=6\\2\sqrt{x}+\sqrt{y}=5\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}\sqrt{x}=\dfrac{6}{5}\\\dfrac{12}{5}+\sqrt{y}=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{36}{25}\\\sqrt{y}=5-\dfrac{12}{5}=\dfrac{13}{5}\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{36}{25}\\y=\left(\dfrac{13}{5}\right)^2=\dfrac{169}{25}\end{matrix}\right.\)
=> Chọn B

a) Ta có:
\(VT=\left(a+b\right)^2-4ab=\left(a^2+2ab+b^2\right)-4ab\\ =a^2+2ab+b^2-4ab=a^2-2ab+b^2\\ =\left(a-b\right)^2=VP\)
=> Đpcm
b) Ta có:
\(VT=\left(a-b\right)^3=\left[-\left(b-a\right)\right]^3=\left[\left(-1\right)\cdot\left(b-a\right)\right]^3\\ =\left(-1\right)^3\left(b-a\right)^3=\left(-1\right)\cdot\left(b-a\right)^3=-\left(b-a\right)^3=VP\)
=> Đpcm
c) Ta có:
\(\left(n+2\right)^2-n^2=\left(n^2+4n+4\right)-n^2\\ =n^2+4n+4-n^2=4n+4=4\left(n+1\right)⋮4\forall n\in N\)
=> Đpcm
a: \(\left(a+b\right)^2-4ab\)
\(=a^2+2ab+b^2-4ab\)
\(=a^2-2ab+b^2=\left(a-b\right)^2\)
b: \(\left(a-b\right)^3=\left[-\left(b-a\right)\right]^3=-\left(b-a\right)^3\)
c: \(\left(n+2\right)^2-n^2=\left(n+2+n\right)\left(n+2-n\right)\)
\(=2\left(2n+2\right)=4\left(n+1\right)⋮4\)

e: \(2^{5x-4}=64\)
=>\(2^{5x-4}=2^6\)
=>5x-4=6
=>5x=10
=>x=10/5=2
f: \(2^{3x+2}=4^{x+6}\)
=>\(2^{3x+2}=2^{2x+12}\)
=>3x+2=2x+12
=>3x-2x=12-2
=>x=10
g: \(4^x=5\cdot4^3-4\cdot4^3\)
=>\(4^x=4^3\)
=>x=3
h: \(4^{5x-3}=16^{2x-1}\)
=>\(4^{5x-3}=\left(4^2\right)^{2x-1}=4^{4x-2}\)
=>5x-3=4x-2
=>5x-4x=-2+3
=>x=1
i: \(5^{7x-2}=5^{3x+10}\)
=>7x-2=3x+10
=>4x=12
=>x=4
l: \(\dfrac{16}{2^x}=2\)
=>\(2^x=\dfrac{16}{2}=8=2^3\)
=>x=3
m: \(\dfrac{\left(-3\right)^x}{81}=-27\)
=>\(\left(-3\right)^x=\left(-3\right)^3\cdot\left(-3\right)^4=\left(-3\right)^7\)
=>x=7

\(e)2^{5x-4}=64\\ \Rightarrow2^{5x-4}=2^6\\ \Rightarrow5x-4=6\\ \Rightarrow5x=6+4=10\\ \Rightarrow x=\dfrac{10}{5}\\ \Rightarrow x=2\\ f)2^{3x+2}=4^{x+6}\\ \Rightarrow2^{3x+2}=\left(2^2\right)^{x+2}\\ \Rightarrow2^{3x+2}=2^{2x+4}\\ \Rightarrow3x+2=2x+4\\ \Rightarrow3x-2x=4-2\\ \Rightarrow x=2\\ g)4^x=5\cdot4^3-4\cdot4^3\\ \Rightarrow4^x=4^3\cdot\left(5-4\right)\\ \Rightarrow4^x=4^3\\ \Rightarrow x=3\\ h)4^{5x-3}=16^{2x-1}\\ \Rightarrow4^{5x-3}=\left(4^2\right)^{2x-2}\\ \Rightarrow4^{5x-3}=4^{4x-4}\\ \Rightarrow5x-3=4x-4\\ \Rightarrow5x-4x=-4+3\\ \Rightarrow x=-1\\ i)5^{7x-2}=5^{3x+10}\\ \Rightarrow7x-2=3x+10\\ \Rightarrow7x-3x=10+2\\ \Rightarrow4x=12\\ \Rightarrow x=12:4\\ \Rightarrow x=3\)

Bài 9:
Bán kính miệng giếng là:
\(1,6:2=0,8\left(m\right)\)
Diện tích miệng giếng tính cả thành giếng:
\(0,8+0,3=1,1\left(m\right)\)
Diện tích miệng giếng là:
\(0,8\times0,8\times3,14=2,0096\left(m^2\right)\)
Diện tích miếng giếng cả thành giếng là:
\(1,1\times1,1\times3,14=3,7994\left(m^2\right)\)
Diện tích thành giếng là:
\(3,7994-2,0096=1,7898\left(m^2\right)\)
ĐS: ...
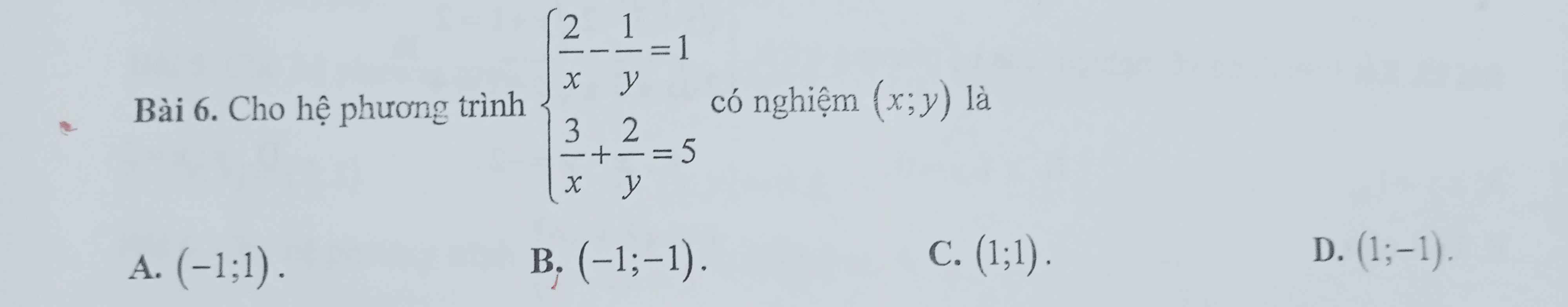
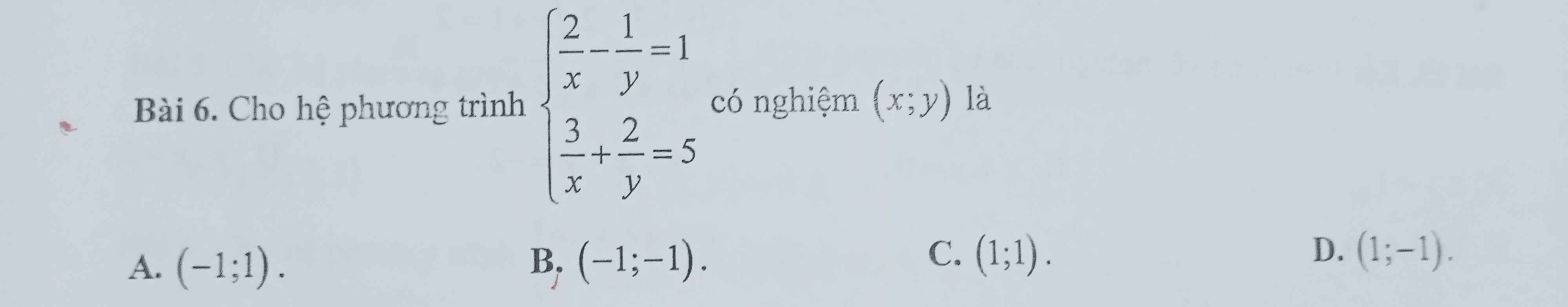
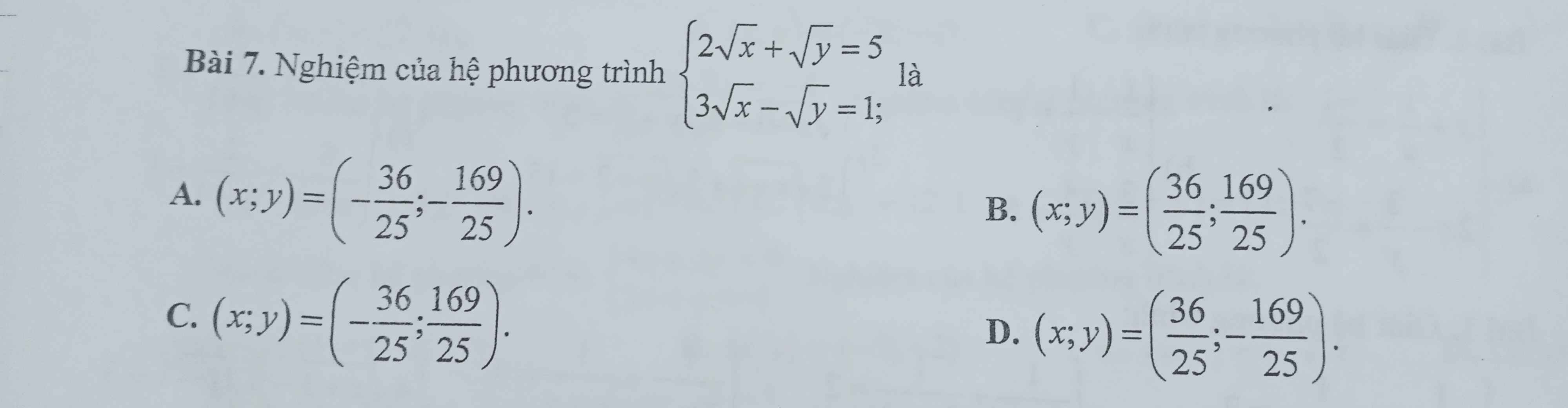
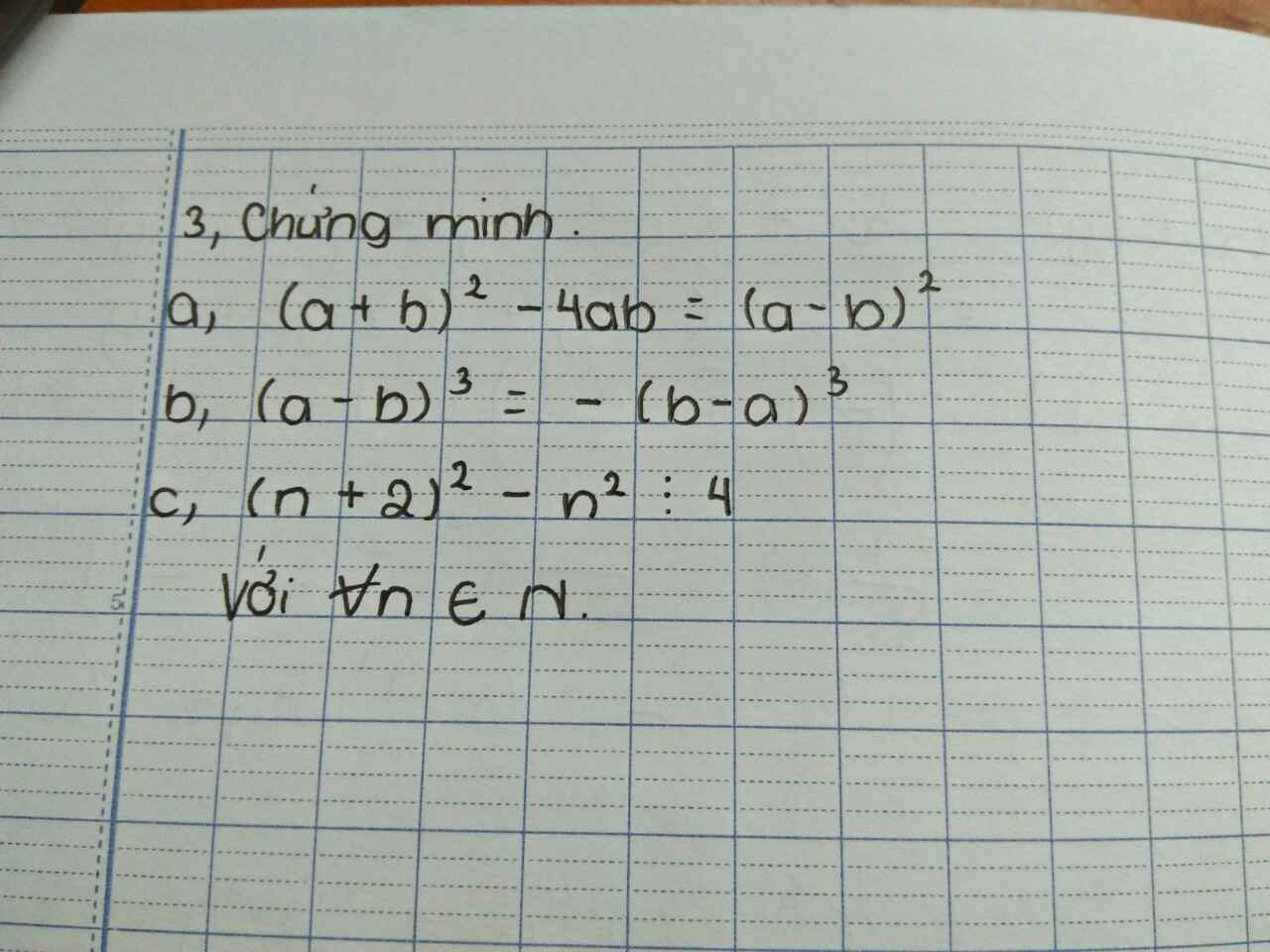

\(a)2^3-50:25+13\cdot7=8-2+91\\ =6+91\\ =97\\ b)60-\left[120-\left(42-33\right)\cdot2\right]\\ =60-\left(120-9\cdot2\right)\\ =60-\left(120-18\right)\\ =60-102\\ =-42\\ c)3^{17}:3^{15}+8\cdot3\\ =3^{17-15}+24\\ =3^2+24\\ =9+24\\ =33\\ d)12:\left\{390:\left[500-\left(125+35\cdot7\right)\right]\right\}\\ =12:\left\{390:\left[500-\left(125+245\right)\right]\right\}\\ =12:\left[390:\left(500-370\right)\right]\\ =12:\left(390:130\right)\\ =12:3=4\)
e: \(72^3\cdot49-72^2\cdot9\)
\(=72^2\left(72\cdot49-9\right)\)
\(=5184\cdot3519=18242496\)
f: \(\dfrac{2^3+2^4+2^5}{7^2}=\dfrac{2^3\left(1+2+2^2\right)}{7^2}=\dfrac{8\cdot7}{49}=\dfrac{8}{7}\)
g: \(\dfrac{15^{22}\cdot7^{18}}{7^{20}\cdot15^{21}}=\dfrac{15^{22}}{15^{21}}\cdot\dfrac{7^{18}}{7^{20}}=\dfrac{15}{7^2}=\dfrac{15}{49}\)