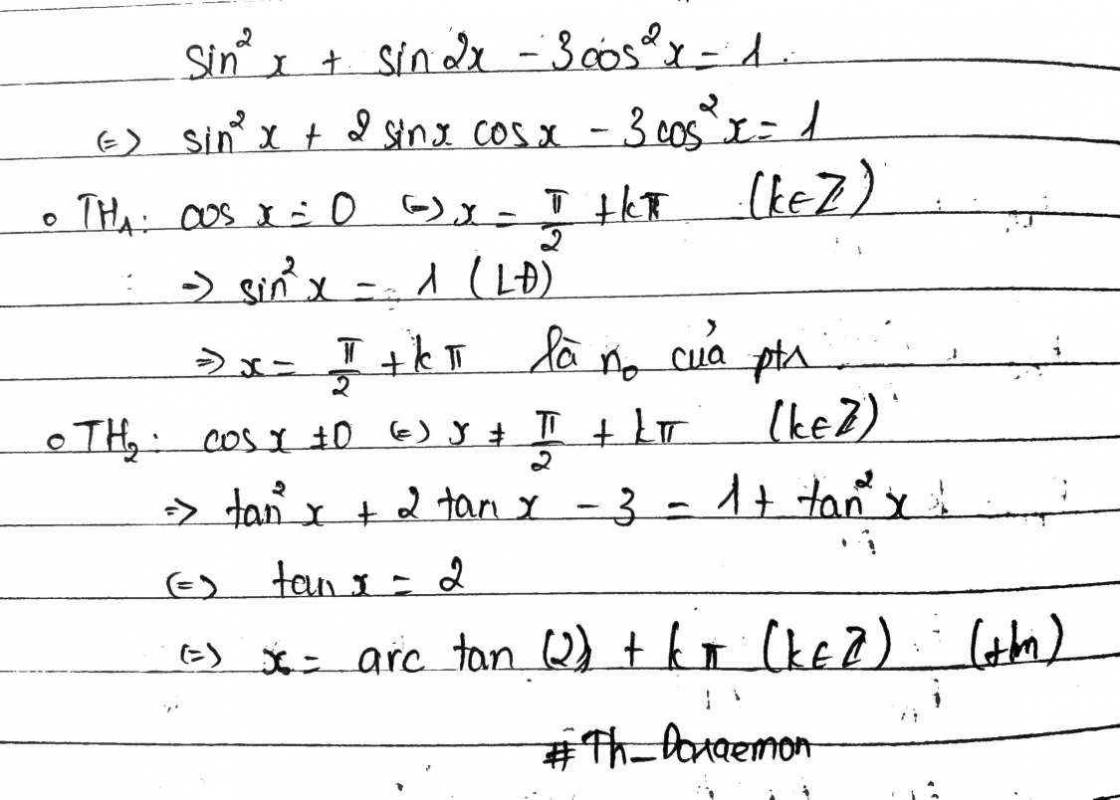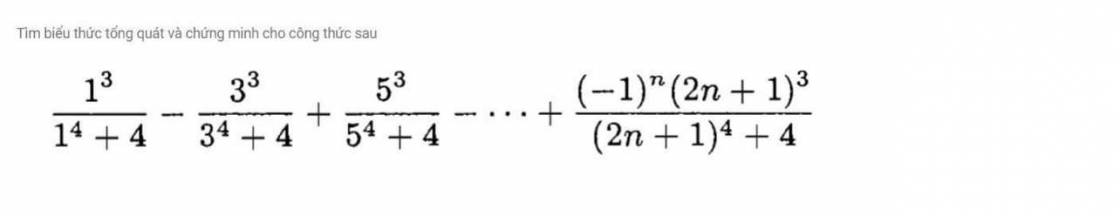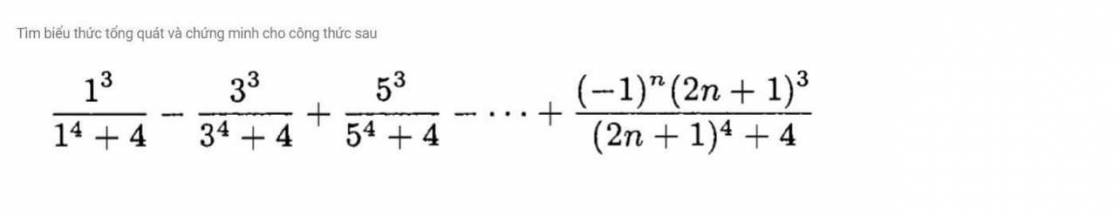\(sin3x=sinx\)

\(\Leftrightarrow\left[{}\begin{matrix}3x=x+k2\pi\\3x=\pi-x+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=k\pi\\x=\dfrac{\pi}{4}+\dfrac{k\pi}{2}\end{matrix}\right.\)

\(\sin3x-\sin x=0\)

\(\Leftrightarrow\sin3x=\sin x\)

\(\Leftrightarrow\left[{}\begin{matrix}3x=x+k2\pi\\3x=\pi-x+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}2x=k2\pi\\4x=\pi+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=k\pi\\x=\dfrac{\pi}{4}+\dfrac{k\pi}{2}\end{matrix}\right.\)

\(\Leftrightarrow sin^2x+2sinx.cosx-3cos^2x=1\)

Nhận thấy \(cosx=0\) không phải nghiệm

Với \(cosx\ne0\) chia 2 vế cho \(cos^2x\)

\(\Rightarrow tan^2x+2tanx-3=\dfrac{1}{cos^2x}\)

\(\Leftrightarrow tan^2x+2tanx-3=1+tan^2x\)

\(\Leftrightarrow tanx=2\)

\(\Rightarrow x=arctan\left(2\right)+k\pi\)

\(a.cosB=b.cosA\)

\(\Leftrightarrow a.\dfrac{a^2+c^2-b^2}{2ac}=b.\dfrac{b^2+c^2-a^2}{2bc}\)

\(\Rightarrow a^2+c^2-b^2=b^2+c^2-a^2\)

\(\Leftrightarrow a^2=b^2\)

\(\Rightarrow a=b\)

Hay tam giác ABC cân tại C

Bài giải của bạn có 2 vấn đề: 1. đề yêu cầu có ít nhất 1 nữ (nghĩa là có thể 1, 2 hoặc 3 nữ đều được) chứ không phải "có đúng 1 nữ" như lời giải của bạn. 2, khi chọn 2 bạn còn lại thì do 2 người này ko phân biệt gì về chức vụ (nghĩa là ko xếp thứ tự) nên phải sử dụng tổ hợp, cách tính của bạn về bản chất là sử dụng chỉnh hợp, gấp đôi về số cách chọn.

Cách giải đúng: chọn 2 bạn nam và xếp thứ tự đội trưởng, đội phó: \(A_{15}^2\) cách

Chọn 3 bạn từ 18 bạn còn lại sao cho ko có nữ nào (nghĩa là cả 3 toàn là nam, về bản chất là chọn 3 nam từ 13 nam còn lại): \(C_{13}^3\) cách

Chọn 3 bạn từ 18 bạn còn lại 1 cách bất kì: \(C_{18}^3\) cách

\(\Rightarrow\) Chọn 3 bạn sao cho có ít nhất 1 nữ: \(C_{18}^3-C_{13}^3\)

Số cách lập đội cờ đỏ: \(A_{15}^2.\left(C_{18}^3-C_{13}^3\right)=111300\) cách

Nãy giờ em thắc mắc quá em cảm ơn nhiều ạ.

À còn đoạn chọn 2 bạn còn lại em dùng tổ hợp C 2 17 ạ, em viết nhầm ạ :(