3 đội xe tải cùng vận chuyển 1 lượng hàng hóa như nhau .Đội thứ nhất vận chuyển trong 2 giờ ,đội thứ 2 vận chuyển trong 2,5 giờ và đội thứ 3 trong 3 giờ .Biết đội thứ nhất có nhiều hơn đội thứ 3 là 10 xe .Tính số xe của mỗi đội(lượng hàng hóa mỗi xe chở được là như nhau)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(-\left(2x-4\right)\left(x+2\right)+\left(x+2\right)^2+\left(x-2\right)^2-4x^2-1-4x=-3\)
=>\(-2\left(x^2-4\right)+x^2+4x+4+x^2-4x+4-4x^2-1-4x=-3\)
=>\(-2x^2+8-2x^2-4x+7+3=0\)
=>\(-4x^2-4x+18=0\)
=>\(x=\dfrac{-1\pm\sqrt{19}}{2}\)
b: \(\left(4x-1\right)^2-16\left(x+1\right)\left(x+3\right)=25\)
=>\(16x^2-8x+1-16\left(x^2+4x+3\right)-25=0\)
=>\(16x^2-8x-24-16x^2-64x-48=0\)
=>-72x-72=0
=>x=-1
c: \(\left(3x-7\right)^2=9\left(3x-7\right)\left(x+5\right)+694\)
=>\(9\left(3x^2+15x-7x-35\right)+694=9x^2-42x+49\)
=>\(27x^2+72x-315+694-9x^2+42x-49=0\)
=>\(18x^2+114x+330=0\)
=>\(x\in\varnothing\)
d: \(\left(2x-1\right)^2+\left(x+3\right)^2=5\left(x+7\right)\left(x-7\right)-3x\)
=>\(4x^2-4x+1+x^2+6x+9=5\left(x^2-49\right)-3x\)
=>\(5x^2+2x+10-5x^2+245+3x=0\)
=>5x+255=0
=>x+51=0
=>x=-51

- Cách 1: $A=\{17;18;19;20;21;22;23\}$
- Cách 2: $A=\{x\in \mathbb{N}^*|17< x\le 23\}$

\(\left(-15\right)\times2-240-6+36:\left(-6\right)\times2\)
\(=-\left(15\times2\right)-240-6+\left[-\left(36:6\right)\times2\right]\)
\(=\left(-30\right)-240-6+\left[-6\times2\right]\)
\(=\left(-30\right)-240-6+\left(-12\right)\)
\(=-270-6+\left(-12\right)\)
\(=-276+\left(-12\right)\)
\(=-288\)

Bài 7
1)
\(A=8\left(3^2+1\right)\left(3^4+1\right)...\left(3^{16}+1\right)\\ =\left(3^2-1\right)\left(3^2+1\right)\left(3^4+1\right)....\left(3^{16}+1\right)\\ =\left(3^4-1\right)\left(3^4+1\right)\left(3^8+1\right)\left(3^{16}+1\right)\\ =\left(3^8-1\right)\left(3^8+1\right)\left(3^{16}+1\right)\\ =\left(3^{16}-1\right)\left(3^{16}+1\right)\\ =3^{32}-1\)
2)
\(B=\left(1-3\right)\left(3+1\right)\left(3^2+1\right)\left(3^4+1\right)...\left(3^{16}+1\right)\\ =-\left(3-1\right)\left(3+1\right)\left(3^2+1\right)\left(3^4+1\right)...\left(3^{16}+1\right)\\ =-\left(3^2-1\right)\left(3^2+1\right)\left(3^4+1\right)...\left(3^{16}+1\right)\\ =-\left(3^4-1\right)\left(3^4+1\right)\left(3^8+1\right)\left(3^{16}+1\right)\\ =-\left(3^8-1\right)\left(3^8+1\right)\left(3^{16}+1\right)\\ =-\left(3^{16}-1\right)\left(3^{16}+1\right)\\ =-\left(3^{32}-1\right)\\ =1-3^{32}\)

1) TXĐ: \(D=ℝ\)
\(9^x+3.6^x=4^{x+1}\)
\(\Leftrightarrow9^x-4.4^x+3.6^x=0\)
\(\Leftrightarrow\dfrac{9^x}{4^x}-4+3.\dfrac{6^x}{4^x}=0\)
\(\Leftrightarrow\left(\dfrac{9}{4}\right)^x+3\left(\dfrac{6}{4}\right)^x-4=0\)
\(\Leftrightarrow\left[\left(\dfrac{3}{2}\right)^2\right]^x+3\left(\dfrac{3}{2}\right)^x-4=0\)
\(\Leftrightarrow\left[\left(\dfrac{3}{2}\right)^x\right]^2+3\left(\dfrac{3}{2}\right)^x-4=0\)
\(\Leftrightarrow\left[\left(\dfrac{3}{2}\right)^x-1\right]\left[\left(\dfrac{3}{2}\right)^x+4\right]=0\)
\(\Leftrightarrow\left(\dfrac{3}{2}\right)^x=1\) (vì \(\left(\dfrac{3}{2}\right)^x>0\))
\(\Leftrightarrow x=0\)
Vậy tập nghiệm của pt đã cho là \(S=\left\{0\right\}\)
2)
a) \(D=ℝ\)
Với \(m=1\) thì (1) thành:
\(\left(\sqrt{2+\sqrt{3}}\right)^{\left|x\right|}+\left(\sqrt{2-\sqrt{3}}\right)^{\left|x\right|}=4\)
Để ý rằng \(\sqrt{2+\sqrt{3}}.\sqrt{2-\sqrt{3}}=1\) \(\Leftrightarrow\sqrt{2-\sqrt{3}}=\dfrac{1}{\sqrt{2+\sqrt{3}}}\)
Do đó pt \(\Leftrightarrow\left(\sqrt{2+\sqrt{3}}\right)^{\left|x\right|}+\left(\dfrac{1}{\sqrt{2+\sqrt{3}}}\right)^{\left|x\right|}-4=0\)
Đặt \(\left(\sqrt{2+\sqrt{3}}\right)^{\left|x\right|}=t\left(t\ge1\right)\) thì pt thành:
\(t+\dfrac{1}{t}-4=0\)
\(\Leftrightarrow t^2-4t+1=0\)
\(\Leftrightarrow\left[{}\begin{matrix}t=2+\sqrt{3}\left(nhận\right)\\t=2-\sqrt{3}\left(loại\right)\end{matrix}\right.\)
Vậy \(\left(\sqrt{2+\sqrt{3}}\right)^{\left|x\right|}=2+\sqrt{3}\)
\(\Leftrightarrow\left|x\right|=2\)
\(\Leftrightarrow x=\pm2\)
Vậy tập nghiệm của pt đã cho là \(S=\left\{\pm2\right\}\)]
2b) Đặt \(f\left(x\right)=\left(\sqrt{2+\sqrt{3}}\right)^{\left|x\right|}+\left(\sqrt{2-\sqrt{3}}\right)^{\left|x\right|}\)
\(f\left(x\right)=\left(\sqrt{2+\sqrt{3}}\right)^{\left|x\right|}+\dfrac{1}{\left(\sqrt{2+\sqrt{3}}\right)^{\left|x\right|}}\)
Đặt \(\left(\sqrt{2+\sqrt{3}}\right)^{\left|x\right|}=t\left(t\ge1\right)\) thì \(f\left(x\right)=g\left(t\right)=t+\dfrac{1}{t}\)
\(g'\left(t\right)=1-\dfrac{1}{t^2}\ge0,\forall t\ge1\)
Lập BBT, ta thấy để \(g\left(t\right)=4m\) có nghiệm thì \(t\ge1\). Tuy nhiên, với \(t>1\) thì sẽ có 2 số \(x\) thỏa mãn \(\left(\sqrt{2+\sqrt{3}}\right)^{\left|x\right|}=t\) (là \(\log_{\sqrt{2+\sqrt{3}}}t\)
và \(-\log_{\sqrt{2+\sqrt{3}}}t\))
Với \(t=1\), chỉ có \(x=0\) là thỏa mãn. Như vậy, để pt đã cho có nghiệm duy nhất thì \(t=1\)
\(\Leftrightarrow m=g\left(1\right)=2\)
Vậy \(m=2\)

Bài 14:
c)
\(H=\dfrac{\dfrac{3}{7}-\dfrac{3}{17}+\dfrac{3}{37}}{\dfrac{5}{7}-\dfrac{5}{17}+\dfrac{5}{37}}+\dfrac{\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{4}-\dfrac{1}{5}}{\dfrac{10}{2}-\dfrac{10}{3}+\dfrac{10}{4}-\dfrac{10}{5}}\\ =\dfrac{3\left(\dfrac{1}{7}-\dfrac{1}{17}+\dfrac{1}{37}\right)}{5\left(\dfrac{1}{7}-\dfrac{1}{17}+\dfrac{1}{37}\right)}+\dfrac{\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{4}-\dfrac{1}{5}}{10\left(\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{4}-\dfrac{1}{5}\right)}\\ =\dfrac{3}{5}+\dfrac{1}{10}\\ =\dfrac{6}{10}+\dfrac{1}{10}\\ =\dfrac{7}{10}\)
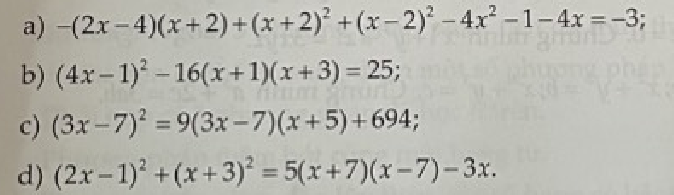

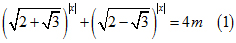 với m là tham số.
với m là tham số.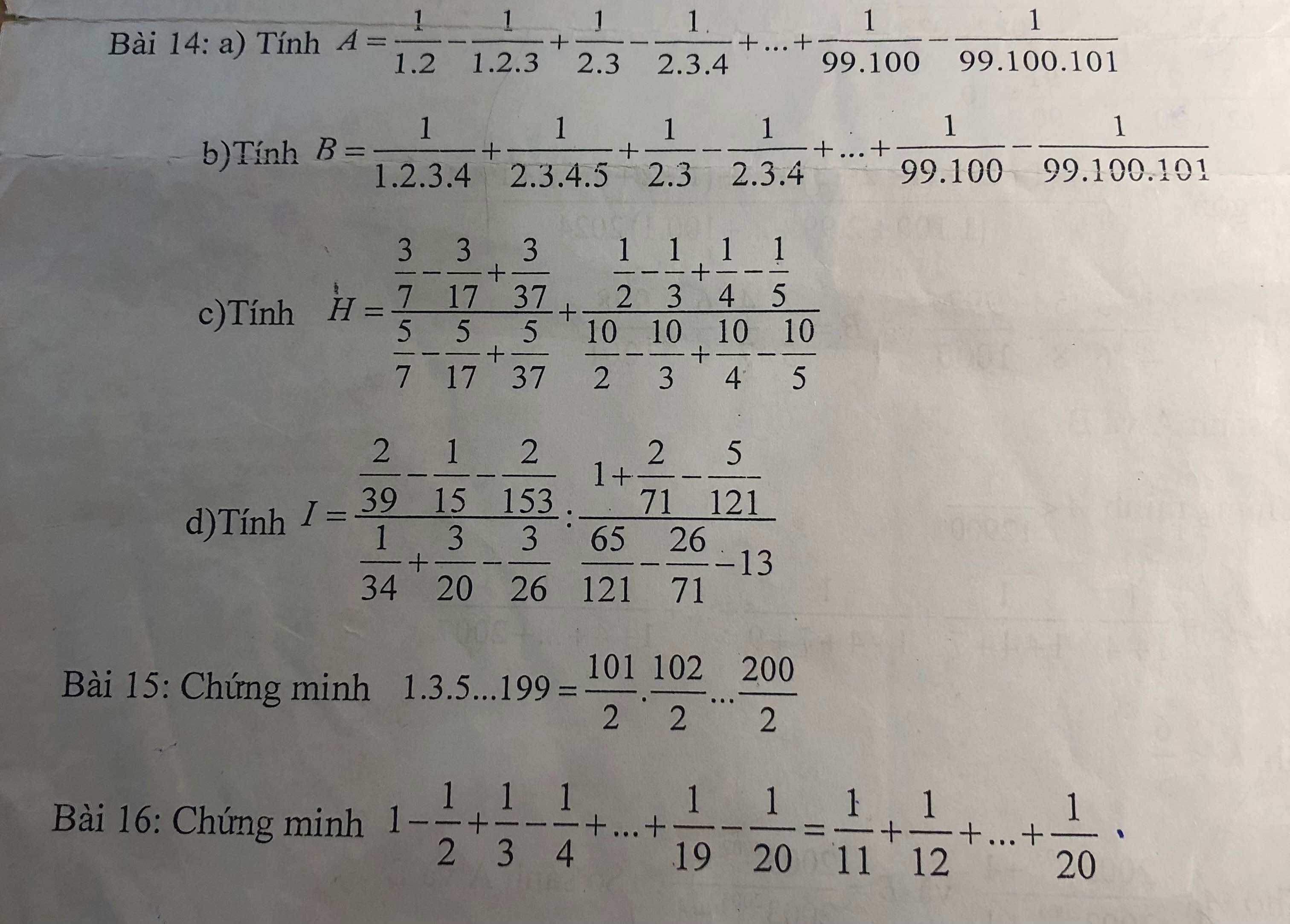
Gọi số xe của đội thứ nhất, thứ hai, thứ ba lần lượt là x,y,z (xe)
Điều kiện: \(x,y,z\inℕ^∗\)
Ta có:
+) Vì đội thứ nhất nhiều hơn đội thứ ba là 10 xe nên:
\(x-z=10\)
+) Vì cùng một lượng hàng hóa thì số xe chở tỉ lệ nghịch với thời gian chở nên:
\(2x=2,5y=3z\Rightarrow\dfrac{2x}{30}=\dfrac{2,5y}{30}=\dfrac{3z}{30}\Rightarrow\dfrac{x}{15}=\dfrac{y}{12}=\dfrac{z}{10}\)
Áp dụng tính chất dãy tỉ số bằng nhau kết hợp \(x-z=10\) được:
\(\dfrac{x}{15}=\dfrac{y}{12}=\dfrac{z}{10}=\dfrac{x-z}{15-10}=\dfrac{10}{5}=2\)
Do đó:
\(\left\{{}\begin{matrix}x=15\cdot2=30\\y=12\cdot2=24\\z=10\cdot2=20\end{matrix}\right.\) (thỏa mãn điều kiện)
Vậy...