
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a)\dfrac{1}{2}x+199=127\cdot36+36\cdot73-30\cdot40\\\dfrac{ 1}{2}x+199=36\cdot\left(127+73\right)-30\cdot40\\ \dfrac{1}{2}x+199=36\cdot200-1200\\ \dfrac{1}{2}x+199=7200-1200\\ \dfrac{1}{2}x+199=6000\\ \dfrac{1}{2}x=6000-199\\ \dfrac{1}{2}x=5801\\ x=5801:\dfrac{1}{2}=11602\)
\(b)\dfrac{3}{2}:x+\dfrac{1}{3}=\dfrac{19}{21}\cdot\dfrac{25}{3}-\dfrac{16}{21}\cdot\dfrac{25}{3}+\dfrac{1}{7}\\ \dfrac{3}{2}:x+\dfrac{1}{3}=\dfrac{25}{3}\cdot\left(\dfrac{19}{3}-\dfrac{16}{3}\right)+\dfrac{1}{7}\\ \dfrac{3}{2}:x+\dfrac{1}{3}=\dfrac{25}{3}+\dfrac{1}{7}\\ \dfrac{3}{2}:x=\dfrac{25}{3}-\dfrac{1}{3}+\dfrac{1}{7}\\ \dfrac{3}{2}:x=8+\dfrac{1}{7}\\ \dfrac{3}{2}:x=\dfrac{57}{7}\\ x=\dfrac{3}{2}:\dfrac{57}{7}\\ x=\dfrac{21}{114}\)
\(c)\left(x-\dfrac{1}{2025}\right):\dfrac{1}{2}=\dfrac{\dfrac{2023}{3}-\dfrac{2023}{5}-\dfrac{2023}{9}}{\dfrac{2025}{6}-\dfrac{2025}{10}-\dfrac{2025}{18}}\\ \left(x-\dfrac{1}{2025}\right):\dfrac{1}{2}=\dfrac{\dfrac{4046}{6}-\dfrac{4046}{10}-\dfrac{4046}{18}}{2025\left(\dfrac{1}{6}-\dfrac{1}{10}-\dfrac{1}{9}\right)}\\ \left(x-\dfrac{1}{2025}\right):\dfrac{1}{2}=\dfrac{4046\left(\dfrac{1}{6}-\dfrac{1}{10}-\dfrac{1}{9}\right)}{2025\left(\dfrac{1}{6}-\dfrac{1}{10}-\dfrac{1}{9}\right)}\\ \left(x-\dfrac{1}{2025}\right):\dfrac{1}{2}=\dfrac{4046}{2025}\\ x-\dfrac{1}{2025}=\dfrac{4046}{2025}\cdot\dfrac{1}{2}\\ x-\dfrac{1}{2025}=\dfrac{2023}{2025}\\ x=\dfrac{2023}{2025}+\dfrac{1}{2025}\\ x=\dfrac{2024}{2025}\)

\(a)\left[\left(1\dfrac{2}{3}\right)^2\right]^3\\ =\left(1\dfrac{2}{3}\right)^{2\cdot3}\\ =\left(\dfrac{5}{3}\right)^6\\ b)\left(-0,18^3\right)^7\\=\left(-0,18\right)^{3\cdot7}\\ =\left(-0,18\right)^{21}\\ c)\left(\dfrac{1}{3^2}\right)^6\\ =\left[\left(\dfrac{1}{3}\right)^2\right]^6\\ =\left(\dfrac{1}{3}\right)^{2\cdot6}\\ =\left(\dfrac{1}{3}\right)^{12}\)

\(\left|x+\dfrac{1}{1\cdot3}\right|+\left|x+\dfrac{1}{3\cdot5}\right|+...+\left|x+\dfrac{1}{197\cdot199}\right|=100x\)
Số lượng số hạng là: \(\left(199-3\right):2+1=99\) (số hạng)
TH1: \(x\ge-\dfrac{1}{197\cdot199}\)
\(=>\left(x+\dfrac{1}{1\cdot3}\right)+\left(x+\dfrac{1}{3\cdot5}\right)+...+\left(x+\dfrac{1}{197\cdot199}\right)=100x\\ =>\left(x+x+...+x\right)+\left(\dfrac{1}{1\cdot3}+\dfrac{1}{3\cdot5}+...+\dfrac{1}{197\cdot199}\right)\\ =>99x+\dfrac{1}{2}\left(\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+...+\dfrac{2}{197\cdot199}\right)\\ =>100x-99x=\dfrac{1}{2}\cdot\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{197}-\dfrac{1}{199}\right)\\ =>x=\dfrac{1}{2}\cdot\left(1-\dfrac{1}{199}\right)=\dfrac{1}{2}\cdot\dfrac{198}{199}\\ =>x=\dfrac{99}{199}\left(tm\right)\)
TH2: \(x\le-\dfrac{1}{1\cdot3}\)
\(=>-\left(x+\dfrac{1}{1\cdot3}\right)-\left(x+\dfrac{1}{3\cdot5}\right)-...-\left(x+\dfrac{1}{197\cdot199}\right)=100x\\ =>-\left[\left(x+x+...+x\right)+\left(\dfrac{1}{1\cdot3}+\dfrac{1}{3\cdot5}+...+\dfrac{1}{197\cdot199}\right)\right]=100x\\ =>-\left[99x+\dfrac{1}{2}\left(\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+...+\dfrac{2}{197\cdot199}\right)\right]=100\\ =>-99x-\dfrac{1}{2}\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{197}-\dfrac{1}{199}\right)=100x\\ =>100x+99x=-\dfrac{1}{2}\left(1-\dfrac{1}{199}\right)\\ =>199x=-\dfrac{1}{2}\cdot\dfrac{198}{199}\\ =>199x=-\dfrac{99}{199}\\ =>x=-\dfrac{99}{199}:199=-\dfrac{99}{39061}\left(ktm\right)\)
Vậy: `x=99/199`

\(\dfrac{4}{\sqrt{5}+\sqrt{3}}-\sqrt{20}\\ =\dfrac{4\left(\sqrt{5}-\sqrt{3}\right)}{\left(\sqrt{5}+\sqrt{3}\right)\left(\sqrt{5}-\sqrt{3}\right)}-\sqrt{20}\\ =\dfrac{4\left(\sqrt{5}-\sqrt{3}\right)}{\left(\sqrt{5}\right)^2-\left(\sqrt{3}\right)^2}-\sqrt{2^2\cdot5}\\ =\dfrac{4\left(\sqrt{5}-\sqrt{3}\right)}{5-3}-2\sqrt{5}\\ =\dfrac{4\left(\sqrt{5}-\sqrt{3}\right)}{2}-2\sqrt{5}\\ =2\left(\sqrt{5}-\sqrt{3}\right)-2\sqrt{5}\\ =2\sqrt{5}-2\sqrt{3}-2\sqrt{5}\\ =-2\sqrt{3}\)

\(\sqrt{5+2\sqrt{6}}-\sqrt{5-2\sqrt{6}}\\ =\sqrt{\left(\sqrt{3}\right)^2+2\cdot\sqrt{3}\cdot\sqrt{2}+\left(\sqrt{2}\right)^2}-\sqrt{\left(\sqrt{3}\right)^2-2\cdot\sqrt{3}\cdot\sqrt{2}+\left(\sqrt{2}\right)^2}\\ =\sqrt{\left(\sqrt{3}+\sqrt{2}\right)^2}-\sqrt{\left(\sqrt{3}-\sqrt{2}\right)^2}\\ =\sqrt{3}+\sqrt{2}-\sqrt{3}+\sqrt{2}\\ =2\sqrt{2}\)

Bài 3:
\(a)\left(x+2\right)\left(x+3\right)-\left(x-2\right)\left(x+5\right)=0\\ \Leftrightarrow x^2+3x+2x+6-\left(x^2+5x-2x-10\right)=0\\ \Leftrightarrow x^2+5x+6-x^2-3x+10=0\\ \Leftrightarrow2x+16=0\\ \Leftrightarrow2x=-16\\ \Leftrightarrow x=-\dfrac{16}{2}=-8\\ b)\left(x-3\right)\left(x-2\right)-\left(x+1\right)\left(x-5\right)=0\\ \Leftrightarrow\left(x^2-2x-3x+6\right)-\left(x^2-5x+x-5\right)=0\\ \Leftrightarrow x^2-5x+6-x^2+4x+5=0\\ \Leftrightarrow-x+11=0\\ \Leftrightarrow x=11\\ c)x\left(2x-5\right)-2x\left(x-6\right)=42\\ \Leftrightarrow2x^2-5x-2x^2+12x=42\\ \Leftrightarrow7x=42\\ \Leftrightarrow x=\dfrac{42}{7}\\ \Leftrightarrow x=6\\ d)\left(x-1\right)\left(2x+3\right)-2x\left(x-1\right)=0\\ \Leftrightarrow\left(x-1\right)\left(2x+3-2x\right)=0\\ \Leftrightarrow3\left(x-1\right)=0\\ \Leftrightarrow x-1=0\\ \Leftrightarrow x=1\)
Bài 2:
b: 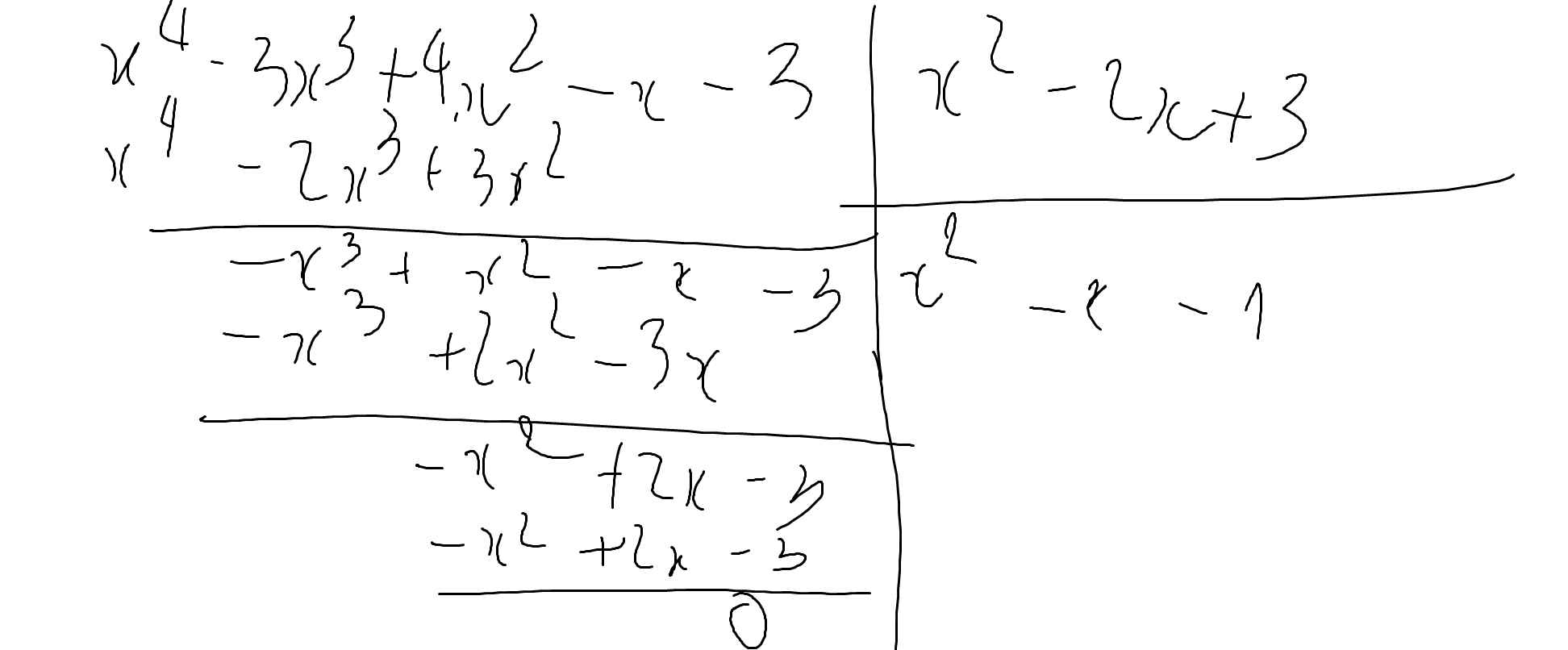
c:
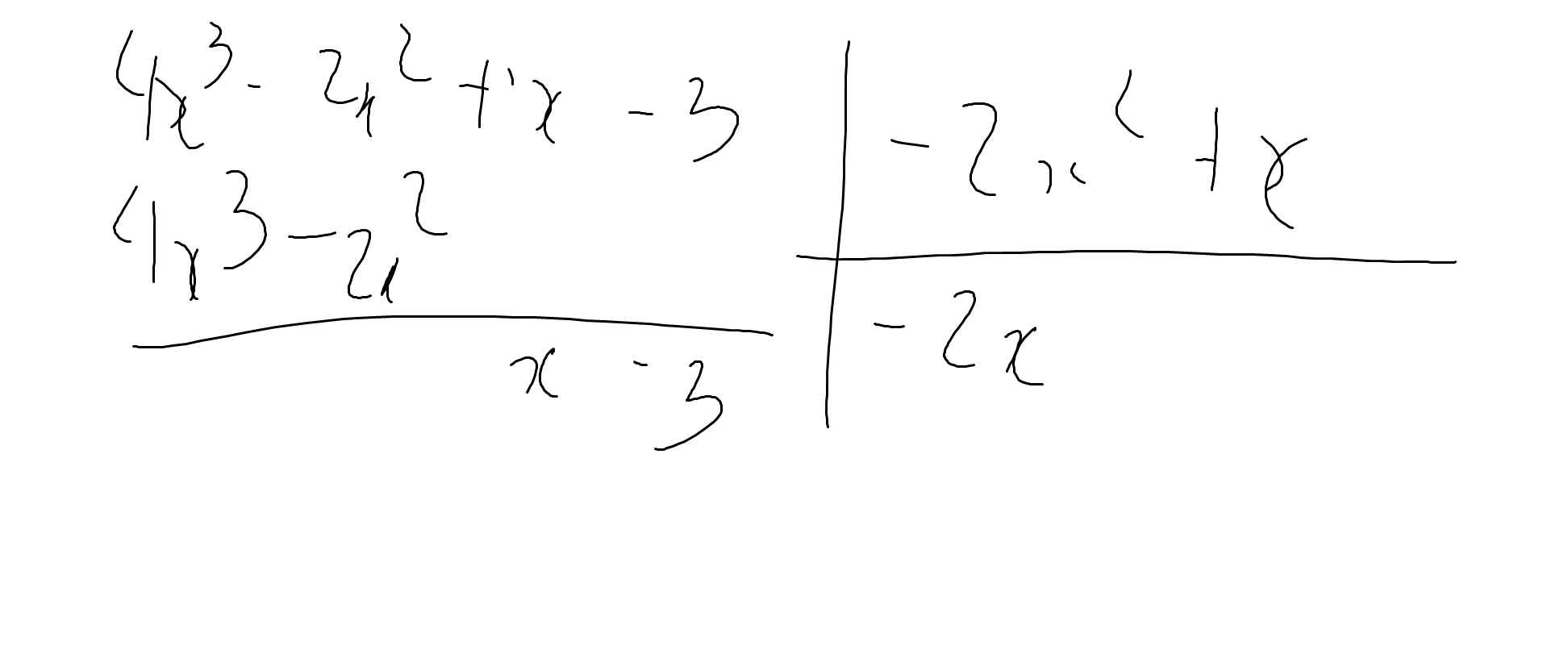
d:
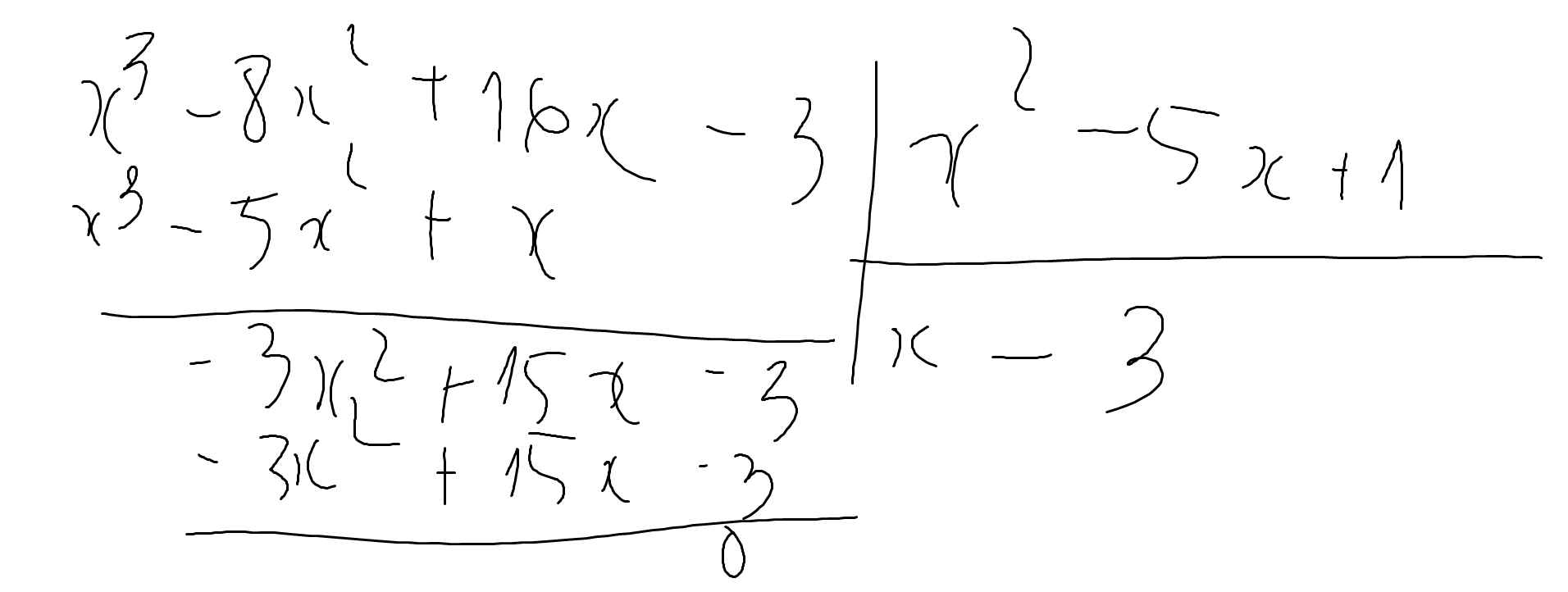
Bài 4:
a: \(A\left(x\right)=x^7-3x^2-x^5+x^4-x^2+2x-7\)
\(=x^7-x^5+x^4+\left(-3x^2-x^2\right)+2x-7\)
\(=x^7-x^5+x^4-4x^2+2x-7\)
\(B\left(x\right)=x-2x^2+x^4-x^5-x^7-4x^2-1\)
\(=-x^7-x^5+x^4+\left(-2x^2-4x^2\right)+x-1\)
\(=-x^7-x^5+x^4-6x^2+x-1\)
b: A(x)+B(x)
\(=x^7-x^5+x^4-4x^2+2x-7-x^7-x^5+x^4-6x^2+x-1\)
\(=-2x^5-10x^2+3x-8\)
A(x)-B(x)
\(=x^7-x^5+x^4-4x^2+2x-7+x^7+x^5-x^4+6x^2-x+1\)
\(=2x^7+2x^2+x-6\)
c: C(x)=A(x)+B(x
=>\(C\left(x\right)=-2x^5-10x^2+3x-8\)
Thay x=-1 vào C(x), ta được:
\(C\left(-1\right)=-2\cdot\left(-1\right)^5-10\cdot\left(-1\right)^2+3\cdot\left(-1\right)-8\)
=2-10-3-8
=-1-10-8=-19

Bài 1:
a) Để căn thức có nghĩa thì:
\(x+1\ge0\Leftrightarrow x\ge-1\)
b) Để căn thức có nghĩa thì:
\(3x-8\ge0\Leftrightarrow3x\ge8\Leftrightarrow x\ge\dfrac{8}{3}\)
c) Để căn thức có nghĩa thì:
\(2x^2+3>0\)
Mà điều này luôn đúng nên căn thức có nghĩa khi x ∈ R
d) Để căn thức có nghĩa thì:
\(16-x^2\ge0\Leftrightarrow\left(4-x\right)\left(4+x\right)\ge0\Leftrightarrow-4\le x\le4\)
Câu 1: B
Câu 2: D
Câu 3: ĐKXĐ: 2x+5>=0
=>2x>=-5
=>\(x>=-\dfrac{5}{2}\)
=>Chọn C
Câu 4: ĐKXĐ: 3-4x>=0
=>-4x>=-3
=>4x<=3
=>\(x< =\dfrac{3}{4}\)
=>Chọn D
Câu 5: \(\sqrt{7}-\sqrt{\left(1-\sqrt{7}\right)^2}\)
\(=\sqrt{7}-\left|1-\sqrt{7}\right|\)
\(=\sqrt{7}-\sqrt{7}+1=1\)
=>Chọn B
Câu 6: \(\sqrt{x^2-6x+9}=\sqrt{\left(x-3\right)^2}=\left|x-3\right|\)
x>=3 nên x-3>=0
=>\(\sqrt{x^2-6x+9}=\left|x-3\right|=x-3\)
=>Chọn B
Câu 7: \(\sqrt{25+x^2+10x}=\sqrt{x^2+10x+25}=\sqrt{\left(x+5\right)^2}=\left|x+5\right|\)
x<-6
=>x+6<0
mà x+5<x+6
nên x+5<0
=>\(\sqrt{25+x^2+10x}=-\left(x+5\right)\)
=>Chọn D
Câu 8: \(M=2x-\sqrt{x^4+2x^2+1}\)
\(=2x-\sqrt{\left(x^2+1\right)^2}\)
\(=2x-\left(x^2+1\right)=-\left(x^2-2x+1\right)=-\left(x-1\right)^2\)
Thay x=11 vào M, ta được:
\(M=-\left(11-1\right)^2=-10^2=-100\)
=>Chọn A
Câu 9: \(\sqrt{x-7}=2\)
=>\(x-7=2^2=4\)
=>x=4+7=11
=>Chọn C
Câu 10: \(\sqrt{a^4b^2}=\sqrt{a^4}\cdot\sqrt{b^2}=a^2\cdot\left|b\right|\)
=>Chọn D
Câu 11: \(\dfrac{1}{2+\sqrt{3}}+\dfrac{1}{2-\sqrt{3}}\)
\(=\dfrac{2-\sqrt{3}+2+\sqrt{3}}{\left(2+\sqrt{3}\right)\left(2-\sqrt{3}\right)}\)
\(=\dfrac{4}{4-3}=4\)
=>Chọn C
Câu 12: A

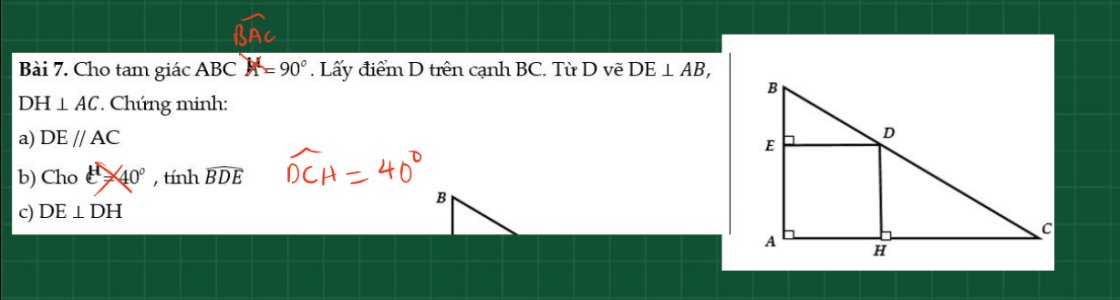
a, Ta có DE vuông AB
AH vuông AB
=> DE // AH
b, Ta có DE // AH => ^BDE = ^ACB ( 2 góc đồng vị )
=> ^BDE = ^DCH = 400
c, Ta có DH vuông AC
AB vuông AC
=> DH // AB
Ta có DH // AB; ED//AH ; ^EAH = ^AED = ^AHD = 900
Vậy tứ giác AEDH là hình vuông
=> DE vuông DH

Số xe cửa hàng nhập về là:
\(80:32\%=250\) (chiếc)
Số xe cửa hàng còn lại là:
`250 - 80 =170` (chiếc)
ĐS: ...
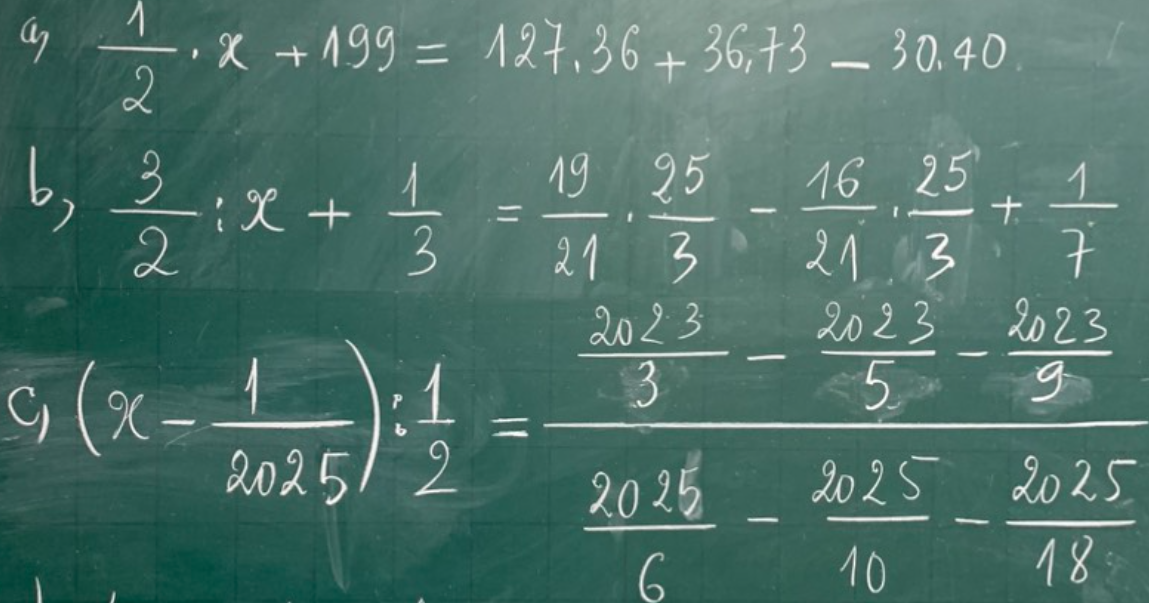
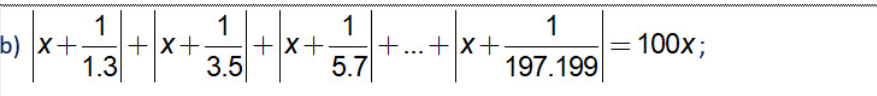
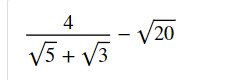
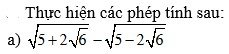



\(a)17\cdot85+15\cdot17-120\\ =17\cdot\left(85+15\right)-120\\ =17\cdot100-120\\ =1700-120\\ =1580\\ b)5\cdot7^2-24:2^3\\ =5\cdot49-24:8\\ =245-3\\ =242\\ c)3^3\cdot22-27\cdot19\\ =27\cdot22-27\cdot19\\ =27\cdot\left(22-19\right)\\ =27\cdot3\\ =81\\ d)-\left|-13\right|+\left(-23\right)\\ =-13+\left(-23\right)\\ =-36\\ e)-\left|-13\right|+\left|-25\right|+\left|12\right|\\ =-13+25+12\\ =12+12\\ =24\\ f)23-\left(12-4^2\right)+\left|15\right|\\ =23-\left(12-16\right)+15\\ =23-\left(-4\right)+15\\ =23+4+15\\ =27+15\\ =42\)