Giải chi tiết:

Bước 1: Xác định phương trình đường thẳng CD
Giả sử:

• Tọa độ của điểm A và B thay đổi, nhưng luôn thỏa mãn điều kiện bài toán.
• Điểm C và D được xác định dựa trên A và B qua một quy tắc cụ thể (ví dụ: trung điểm, hình chiếu, giao điểm đường phân giác...).
• Gọi phương trình đường thẳng CD có dạng:
  \(a x + b y + c = 0 (\text{ph}ụ\&\text{nbsp};\text{thu}ộ\text{c}\&\text{nbsp};\text{v} \overset{ˋ}{\text{a}} \text{o}\&\text{nbsp};\text{t}ọ\text{a}\&\text{nbsp};độ\&\text{nbsp};\text{A},\&\text{nbsp};\text{B})\)

Bước 2: Tìm điểm cố định mà CD luôn đi qua

• Giả định tồn tại điểm cố định \(M \left(\right. x_{0} , y_{0} \left.\right)\) sao cho CD luôn đi qua \(M\) với mọi vị trí của A và B (\(A \neq B\)).
• Thay \(M \left(\right. x_{0} , y_{0} \left.\right)\) vào phương trình CD:
  \(a \left(\right. x_{0} , y_{0} , A , B \left.\right) \cdot x_{0} + b \left(\right. x_{0} , y_{0} , A , B \left.\right) \cdot y_{0} + c \left(\right. x_{0} , y_{0} , A , B \left.\right) = 0 \forall A , B\)
• Phân tích phương trình:
  Biến đổi phương trình về dạng đa thức theo tham số liên quan đến A và B. Để phương trình đúng với mọi A, B, hệ số của các hạng tử chứa tham số phải bằng 0.

Bước 3: Giải hệ phương trình

• Ví dụ: Nếu phương trình có dạng:
  \(\left(\right. m + 1 \left.\right) x_{0} - \left(\right. 2 m - 3 \left.\right) y_{0} + 5 = 0 \forall m\)
• • Tách hệ số của \(m\):
    \(m \left(\right. x_{0} - 2 y_{0} \left.\right) + \left(\right. x_{0} + 3 y_{0} + 5 \left.\right) = 0 \forall m\)
  • Đồng nhất hệ số:
    \(\left{\right. x_{0} - 2 y_{0} = 0 \\ x_{0} + 3 y_{0} + 5 = 0\)
  • Giải hệ:
    \(x_{0} = 2 y_{0} 2 y_{0} + 3 y_{0} + 5 = 0 \textrm{ }\textrm{ } \Longrightarrow \textrm{ }\textrm{ } y_{0} = - 1 \textrm{ }\textrm{ } \Longrightarrow \textrm{ }\textrm{ } x_{0} = - 2\)
  • Kết luận: Điểm cố định là \(M \left(\right. - 2 , - 1 \left.\right)\).

Bước 4: Kiểm tra lại

• Thay \(M \left(\right. x_{0} , y_{0} \left.\right)\) vào phương trình CD với các vị trí khác nhau của A, B để xác nhận tính đúng đắn.

Ví dụ minh họa:
Cho tam giác ABC cố định. Trên AB lấy điểm D di động, trên AC lấy điểm E di động sao cho \(A D = C E\). Chứng minh DE luôn đi qua một điểm cố định.

Giải:

• Bước 1: Chọn hệ trục tọa độ, giả sử \(A \left(\right. 0 , 0 \left.\right)\), \(B \left(\right. 1 , 0 \left.\right)\), \(C \left(\right. 0 , 1 \left.\right)\).
• Bước 2: Gọi \(D \left(\right. t , 0 \left.\right)\) trên AB và \(E \left(\right. 0 , t \left.\right)\) trên AC (vì \(A D = C E = t\)).
• Bước 3: Phương trình DE:
  \(\frac{x - t}{- t} = \frac{y}{t - 0} \textrm{ }\textrm{ } \Longrightarrow \textrm{ }\textrm{ } x + y = t\)
• Bước 4: Phương trình \(x + y = t\) phụ thuộc vào \(t\). Để DE đi qua điểm cố định \(M \left(\right. x_{0} , y_{0} \left.\right)\):
  \(x_{0} + y_{0} = t \forall t \textrm{ }\textrm{ } \Longrightarrow \textrm{ }\textrm{ } x_{0} + y_{0} = 0\)
  Chọn \(M \left(\right. 1 , - 1 \left.\right)\) (nằm trên đường thẳng \(x + y = 0\)).

Kết luận: DE luôn đi qua điểm cố định \(M \left(\right. 1 , - 1 \left.\right)\).

Đáp án:
Đường thẳng CD luôn đi qua điểm cố định \(M \left(\right. x_{0} , y_{0} \left.\right)\) được xác định bằng cách giải hệ phương trình từ phương trình tổng quát của CD145.

Giải chi tiết:

Bước 1: Xác định vị trí các điểm P, I, K, Q
Giả thiết:

• P là trung điểm của AB.
• Q là trung điểm của AC.
• I và K lần lượt là trung điểm của BC và CA.

Bước 2: Tính chất hình học

• Đường trung bình PQ của tam giác ABC song song với BC và có độ dài bằng \(\frac{1}{2} B C\).
• Tứ giác PIKQ là hình bình hành (do PQ // IK và PI // QK).

Bước 3: Tính diện tích PIKQ

• Diện tích hình bình hành PIKQ = \(\frac{1}{2} \times \text{Di}ệ\text{n}\&\text{nbsp};\text{t} \overset{ˊ}{\imath} \text{ch}\&\text{nbsp};\text{tam}\&\text{nbsp};\text{gi} \overset{ˊ}{\text{a}} \text{c}\&\text{nbsp};\text{ABC}\).
• Giả sử tam giác ABC có diện tích \(S_{A B C}\), khi đó:
  \(S_{P I K Q} = \frac{1}{2} S_{A B C}\)

Ví dụ minh họa:
Cho tam giác ABC có diện tích \(20 \textrm{ } \text{cm}^{2}\).

• Diện tích tứ giác PIKQ là:
  \(S_{P I K Q} = \frac{1}{2} \times 20 = 10 \textrm{ } \text{cm}^{2}\)

Kết luận:
Diện tích tứ giác PIKQ bằng một nửa diện tích tam giác ABC nếu các điểm P, I, K, Q là trung điểm của các cạnh134.

Công thức tổng quát:

\(S_{P I K Q} = \frac{1}{2} S_{A B C}\)

Đáp án:
Diện tích tứ giác PIKQ là \(\boxed{\frac{1}{2} S_{A B C}}\).

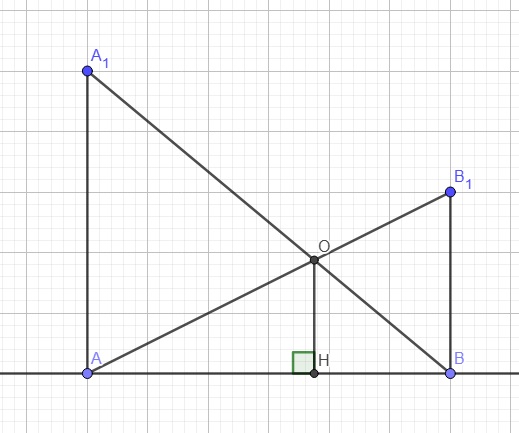
Gọi H là hình chiếu vuông góc của O lên d

\(\Rightarrow AA_1||OH||BB_1\)

Áp dụng định lý Thales trong tam giác \(ABA_1\)

\(\dfrac{OH}{AA_1}=\dfrac{BH}{AB}\)

Áp dụng định lý Thales trong tam giác \(ABB_1\)

\(\dfrac{OH}{BB1}=\dfrac{AH}{AB}\)

\(\Rightarrow\dfrac{OH}{AA_1}+\dfrac{OH}{BB_1}=\dfrac{BH}{AB}+\dfrac{AH}{AB}\)

\(\Rightarrow OH.\left(\dfrac{1}{a}+\dfrac{1}{b}\right)=1\)

\(\Rightarrow OH=\dfrac{a.b}{a+b}\)

Do a, b không đổi \(\Rightarrow OH\) không đổi

Hay khoảng cách từ O đến d không đổi khi A, B chạy trên d

3. Chứng minh công thức:

AF/AB + BE/BC + CN/CA = 1 trong tam giác ABC

Giả thiết:

• Tam giác ABC.
• Các điểm F, E, N lần lượt nằm trên các cạnh AB, BC, CA.

Cách chứng minh:

Trường hợp đặc biệt:
Nếu F, E, N là các điểm chia các cạnh theo cùng một tỉ lệ (ví dụ: F chia AB theo tỉ lệ x, E chia BC theo tỉ lệ y, N chia CA theo tỉ lệ z sao cho x + y + z = 1).

Chứng minh tổng quát:

• Gọi AF = x·AB, BE = y·BC, CN = z·CA, với x, y, z ∈ (0;1).
• Khi đó:
  \(\frac{A F}{A B} + \frac{B E}{B C} + \frac{C N}{C A} = x + y + z\)
• Nếu ba điểm F, E, N chia ba cạnh theo tỉ lệ x, y, z sao cho x + y + z = 1, thì tổng trên bằng 1.

Trường hợp đặc biệt:
Nếu F, E, N là trung điểm các cạnh, thì mỗi phân số đều bằng 1/2, tổng lại là 3/2 ≠ 1.
Vậy công thức đúng khi ba điểm chia ba cạnh theo tỉ lệ x, y, z với x + y + z = 1.

a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có

\(\widehat{HBA}\) chung

Do đó: ΔHBA~ΔABC

b: Xét ΔHBA vuông tại H  và ΔHAC vuông tại H có

\(\widehat{HBA}=\widehat{HAC}\left(=90^0-\widehat{HAB}\right)\)

Do đó: ΔHBA~ΔHAC

=>\(\dfrac{HB}{HA}=\dfrac{HA}{HC}\)

=>\(HA^2=HB\cdot HC\)

c: ΔABC vuông tại A

=>\(AB^2+AC^2=BC^2\)

=>\(BC=\sqrt{3^2+4^2}=5\left(cm\right)\)

ΔBHA~ΔBAC

=>\(\dfrac{S_{BHA}}{S_{BAC}}=\left(\dfrac{BA}{BC}\right)^2=\left(\dfrac{3}{5}\right)^2=\dfrac{9}{25}\)

a) Ta có đcao AH(H thuộc BC)->AH vuông góc với BC->AHB=AHC=90 xét ABH và CBA có AHB=CAB=90 CBA chung ->tg ABH đồng dạng với tg CBA(g-g) b)xét tg ABH vuông tại H có HBA+HAB=90(1) Xét tg ABC có ABC+ACB=90 hayHBA+ACH=90(2) Từ (1) và (2)->HAB=ACH Xét tgHAC và tg HBA có ACH=BAH(cmt) AHC=BHA=90 -> tg HAC đồng dạng với tg HBA(g-g)->AH/HB=CH/AH hay AH2=BH.CH

Giải:

ΔABC ∼ΔA'B'C' ta có:

Góc A = góc A'; Góc B = góc B'; Góc C = Góc C'

Và các tỉ số:

\(\frac{AB}{A^{\prime}B^{\prime}}=\frac{AC}{A^{\prime}C^{\prime}}=\frac{BC}{B^{\prime}C^{\prime}}\)

Vậy khẳng định không đúng là khẳng định:

C. \(\frac{AB}{A^{\prime}B^{\prime}}\) = \(\frac{A^{\prime}C^{\prime}}{AC}\)

Chọn C nha bạn

Giải:

y = (m -2)\(x\) + 2

⇒ (m- 2)\(x\) - y + 2 = 0

Gốc tọa độ O(0; 0)

Khoảng cách từ gốc tọa độ O(0; 0) đến đường thẳng (d) là:

d(O;d) = \(\frac{\left|\left(m-2\right)\right..0-1.0+2\left|\right.}{\sqrt{\left(m-2\right)^2+1}}\) = \(\frac{2}{\sqrt{\left(m-2\right)^2+1}}\)

Khoảng cách từ gốc tọa độ O đến đường thẳng (d) là lớn nhất khi A = \(\frac{2}{\sqrt{\left(m-2\right)^2+1}}\) lớn nhất.

Vì 2 > 0; \(\sqrt{\left(m-2\right)^2+1}\) > 0 ∀ m nên

A lớn nhất khi (m - 2)\(^2\) + 1 là nhỏ nhất.

(m - 2)\(^2\) ≥ 0 ∀ m

(m - 2)\(^2\) + 1 ≥ 1 ∀ m

\(\sqrt{\left(m-2\right)^2+1}\) ≥ 1 ∀ m

A = \(\frac{2}{\sqrt{\left(m-2^{}\right)^2+1}}\) ≤ \(\frac21=2\) dấu bằng xảy khi m - 2 = 0

suy ra m = 2

Vậy khoảng cách từ gốc tọa độ đến đồ thị lớn nhất là \(2\) khi m = 2

B =\(\frac{1}{1.5}\) + \(\frac{1}{5.9}\) + ...+ \(\frac{1}{\left(4n-3\right).\left(4n+1\right)}\)

B = \(\frac14\).(\(\frac{4}{1.5}+\frac{4}{5.9}+\cdots+\frac{4}{\left(4n-3\right).\left(4n+1\right)}\)

B = \(\frac14\).(\(\frac11\) - \(\frac15\) + \(\frac15\) - \(\frac19\) + ... + \(\frac{1}{4n-3}-\frac{1}{4n+1}\))

B = \(\frac14\).(\(\frac11\) - \(\frac{1}{4n+1}\))

B = \(\frac14\).\(\frac{4n}{4n+1}\)

B = \(\frac{n}{4n+1}\)

\(-\dfrac{15x^2y^3}{18x^3y^5}=-\dfrac{15}{18}\cdot\dfrac{x^2}{x^3}\cdot\dfrac{y^3}{y^5}=\dfrac{-5}{6\cdot x\cdot y^2}\)

Bài 2:

a: Khi x=4 thì \(M=\dfrac{4+3}{4-2}=\dfrac{7}{2}\)

b: \(M=\dfrac{2}{3}\)

=>\(\dfrac{x+3}{x-2}=\dfrac{2}{3}\)

=>3(x+3)=2(x-2)

=>3x+9=2x-4

=>3x-2x=-4-9

=>x=-13(nhận)

c: Để M là số nguyên dương thì \(\left\{{}\begin{matrix}x+3⋮x-2\\M>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-2+5⋮x-2\\\dfrac{x+3}{x-2}>0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}5⋮x-2\\\left[{}\begin{matrix}x>2\\x< -3\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-2\in\left\{1;-1;5;-5\right\}\\\left[{}\begin{matrix}x>2\\x< -3\end{matrix}\right.\end{matrix}\right.\)

=>\(x\in\left\{3;7\right\}\)

Bài 3:

ΔMIN vuông tại I

=>\(IM^2+IN^2=MN^2\)

=>\(x=MI=\sqrt{12^2-5^2}=\sqrt{144-25}=\sqrt{119}\left(cm\right)\)

ΔMIP vuông tại I

=>\(IM^2+IP^2=PM^2\)

=>\(y=\sqrt{119+100}=\sqrt{219}\left(cm\right)\)

Bài 4:

a: Xét ΔBAC vuông tại A và ΔBHA vuông tại H có

\(\widehat{ABC}\) chung

Do đó: ΔBAC~ΔBHA

b: Xét ΔHBA vuông tại H và ΔHAC vuông tại H có

\(\widehat{HBA}=\widehat{HAC}\left(=90^0-\widehat{HAB}\right)\)

Do đó: ΔHBA~ΔHAC

=>\(\dfrac{HB}{HA}=\dfrac{HA}{HC}\)

=>\(HA^2=HB\cdot HC\)

c: Xét tứ giác AIHK có \(\widehat{AIH}=\widehat{AKH}=\widehat{KAI}=90^0\)

nên AIHK là hình chữ nhật

=>\(\widehat{AKI}=\widehat{AHI}\)

mà \(\widehat{AHI}=\widehat{ABC}\left(=90^0-\widehat{HAB}\right)\)

nên \(\widehat{AKI}=\widehat{ABC}\)

ΔABC vuông tại A

mà AM là đường trung tuyến

nên MA=MC

=>ΔMAC cân tại M

=>\(\widehat{MAC}=\widehat{MCA}\)

\(\widehat{AKI}+\widehat{MAC}=\widehat{ABC}+\widehat{ACB}=90^0\)

=>AM\(\perp\)IK