 giúp em vs ạ em cảm ơn nhiều
giúp em vs ạ em cảm ơn nhiều
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Giải:
Câu a tự làm
b; Phương trình hoành độ giao điểm của (p) và (d) là:
\(x^2\) = - 2\(x\) + 3
\(x^2\) + 2\(x\) - 3 = 0
a + b + c = 1 + 2 - 3 = 0
Vậy phương trình có hai nghiệm phân biệt lần lượt là:
\(x_1\) = 1; \(x_2\) = - 3
\(x_1\) = 1 ⇒ y1 = 12 = 1; \(x_2\) = - 3 ⇒ y2 = (\(x_2\))2 = (- 3)2 = 9
Vậy (p) cắt (d) tại hai điểm A; B lần lượt có tọa độ là:
A(1; 1); B(-3; 9)

a.
Do MA, MB là các tiếp tuyến \(\Rightarrow\widehat{MAO}=\widehat{MBO}=90^0\)
\(\Rightarrow A,B\) cùng nhìn OM dưới 1 góc vuông nên AOBM nội tiếp
b.
\(C_{\left(O\right)}=2\pi R=10\pi=31,42\left(cm\right)\)
Trong tam giác vuông OAM:
\(cos\widehat{AOM}=\dfrac{OA}{OM}=\dfrac{R}{2R}=\dfrac{1}{2}\Rightarrow\widehat{AOM}=60^0\)
\(\Rightarrow\widehat{AOB}=2\widehat{AOM}=120^0\)
\(\Rightarrow S_{OAB}=S_{\left(O\right)}.\dfrac{120}{360}=\dfrac{\pi.R^2}{3}=\dfrac{5^2.\pi}{3}\approx26,18\)
c.
Ta có \(CM=OM-OC=2R-R=R\)
\(\Rightarrow CM=OC\Rightarrow C\) là trung điểm OM
\(\Rightarrow AC\) là trung tuyến ứng với cạnh huyền trong tam giác vuông OAM
\(\Rightarrow AC=\dfrac{1}{2}OM=R=OA\)
Tương tự có BC là trung tuyến ứng với cạnh huyền trong tam giác vuông OBM
\(\Rightarrow BC=OC=R\)
\(\Rightarrow OA=AC=BC=OB\Rightarrow AOBC\) là hình thoi
Gọi D là giao điểm AB và OC \(\Rightarrow AD\perp OC\) (hai đường chéo hình thoi)
Trong tam giác vuông AOD:
\(sin\widehat{AOD}=\dfrac{AD}{OA}\Rightarrow AD=OA.sin\widehat{AOD}=5.sin60^0=\dfrac{5\sqrt{3}}{2}\left(cm\right)\)
\(\Rightarrow AB=2AD=5\sqrt{3}\) (cm)
\(\Rightarrow S_{AOBC}=\dfrac{1}{2}AD.OC=\dfrac{25\sqrt{3}}{2}\approx21,65\left(cm^2\right)\)


Giải
Gọi số ngày mà tổ đó phải hoàn thành theo kế hoạch là: \(x\) (ngày)
Điều kiện: \(x\) \(\in\) N
Số ngày thực tế đội đó hoàn thành là: \(x\) - 2 (ngày)
Số áo mỗi ngày đội đó làm được theo kế hoạch là: \(\dfrac{1200}{x}\) (chiếc áo)
Số áo mỗi ngày mà đội đó làm được trên thực tế là: \(\dfrac{1200}{x-2}\) (chiếc áo)
Theo bài ra ta có phương trình:
\(\dfrac{1200}{x-2}\) - \(\dfrac{1200}{x}\) = 20
\(\dfrac{60}{x-2}\) - \(\dfrac{60}{x}\) = 1
60\(x\) - 60\(x\) + 120 = \(x^2\) - 2\(x\)
\(x^2\) - 2\(x\) + 1 = 121
(\(x\) - 1)2 = 112
\(\left[{}\begin{matrix}x-1=11\\x-1=-11\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=12\\x=-10\end{matrix}\right.\)
Vì \(x\) > 0 nên \(x\) = 12
Kêt luận số ngày mà đội đó phải hoàn thành theo kế hoạch là 12 ngày.

Gọi thời gian tổ may xong áo theo kế hoạch là \(x(\text{ngày};x\in \mathbb{N}^*)\)
Theo kế hoạch thì mỗi ngày tổ may được: \(\dfrac{1200}{x}\) (chiếc áo)
Thời gian tổ may xong trên thực tế là: \(x-2\) (ngày)
Trên thực tế thì mỗi ngày tổ may được: \(\dfrac{1200}{x-2}\) (chiếc áo)
Do cải tiến kỹ thuật nên mỗi ngày tổ may thêm được 20 chiếc áo, khi đó ta có pt:
\(\dfrac{1200}{x}+20=\dfrac{1200}{x-2}\)
\(\Leftrightarrow1200\cdot\left(\dfrac{1}{x-2}-\dfrac{1}{x}\right)=20\)
\(\Leftrightarrow\dfrac{x-\left(x-2\right)}{x\left(x-2\right)}=\dfrac{20}{1200}\)
\(\Leftrightarrow\dfrac{2}{x^2-2x}=\dfrac{1}{60}\)
\(\Rightarrow x^2-2x=120\)
\(\Leftrightarrow x^2-2x-120=0\)
\(\Leftrightarrow\left(x-1\right)^2-121=0\)
\(\Leftrightarrow\left(x-12\right)\left(x+10\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-12=0\\x+10=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=12\left(tm\right)\\x=-10\left(ktm\right)\end{matrix}\right.\)
Vậy theo kế hoạch tổ phải may số áo trên trong 12 ngày.
Giải
Gọi số ngày mà tổ đó phải hoàn thành theo kế hoạch là: \(x\) (ngày)
Điều kiện: \(x\) \(\in\) N
Số ngày thực tế đội đó hoàn thành là: \(x\) - 2 (ngày)
Số áo mỗi ngày đội đó làm được theo kế hoạch là: \(\dfrac{1200}{x}\) (chiếc áo)
Số áo mỗi ngày mà đội đó làm được trên thực tế là: \(\dfrac{1200}{x-2}\) (chiếc áo)
Theo bài ra ta có phương trình:
\(\dfrac{1200}{x-2}\) - \(\dfrac{1200}{x}\) = 20
\(\dfrac{60}{x-2}\) - \(\dfrac{60}{x}\) = 1
60\(x\) - 60\(x\) + 120 = \(x^2\) - 2\(x\)
\(x^2\) - 2\(x\) + 1 = 121
(\(x\) - 1)2 = 112
\(\left[{}\begin{matrix}x-1=11\\x-1=-11\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=12\\x=-10\end{matrix}\right.\)
Vì \(x\) > 0 nên \(x\) = 12
Kêt luận số ngày mà đội đó phải hoàn thành theo kế hoạch là 12 ngày.

Bài 1:
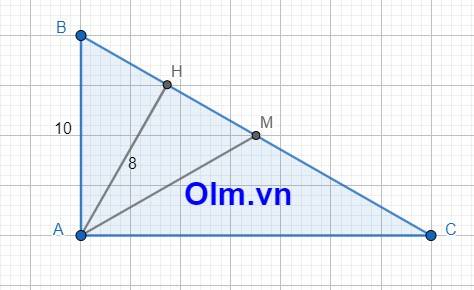
Theo pytago ta có: HB2 + AH2 = AB2
⇒ HB2 = AB2 - AH2
HB2 = 102 - 82 = 36
HB = \(\sqrt{36}\) = 6 (cm)
Xét tam giác ABC và tam giác HBA có:
\(\widehat{BAC}\) = \(\widehat{BHA}\) = 900
\(\widehat{ABC}\) = \(\widehat{HBA}\)
⇒ \(\Delta\) ABC \(\sim\) \(\Delta\) HBA (g - g)
⇒ \(\dfrac{AB}{HB}\) = \(\dfrac{BC}{BA}\)
BC = \(\dfrac{AB}{HB}\) \(\times\) AB
BC = \(\dfrac{10.10}{6}\) = \(\dfrac{50}{3}\) (cm)
SABC = \(\dfrac{1}{2}\)BC \(\times\) AH = \(\dfrac{1}{2}\) \(\times\) \(\dfrac{50}{3}\) \(\times\) 8 = \(\dfrac{200}{3}\) (cm2)
Vì M là trung điểm của tam giác ABC nên
SABM = \(\dfrac{1}{2}\) SABC (hai tam giác có chung chiều cao hạ từ đỉnh A xuống đáy BC và BM = \(\dfrac{1}{2}\) BC)
SABM = \(\dfrac{200}{3}\).\(\dfrac{1}{2}\) = \(\dfrac{100}{3}\) (cm2)
SAHB = \(\dfrac{1}{2}\)AH.HB = \(\dfrac{8.6}{2}\) = 24 (cm2)
SAHB + SAHM = SABM
⇒ SAHM = SABM - SAHB
SAHM = \(\dfrac{100}{3}\) - 24 = \(\dfrac{28}{3}\) (cm2)
Kết luận: BC dài \(\dfrac{50}{3}\) cm; Diện tích tam giác AHM là \(\dfrac{28}{3}\) cm2

Bài 1:
Theo pytago ta có: HB2 + AH2 = AB2
⇒ HB2 = AB2 - AH2
HB2 = 102 - 82 = 36
HB = \(\sqrt{36}\) = 6 (cm)
Xét tam giác ABC và tam giác HBA có:
\(\widehat{BAC}\) = \(\widehat{BHA}\) = 900
\(\widehat{ABC}\) = \(\widehat{HBA}\)
⇒ \(\Delta\) ABC \(\sim\) \(\Delta\) HBA (g - g)
⇒ \(\dfrac{AB}{HB}\) = \(\dfrac{BC}{BA}\)
BC = \(\dfrac{AB}{HB}\) \(\times\) AB
BC = \(\dfrac{10.10}{6}\) = \(\dfrac{50}{3}\) (cm)
SABC = \(\dfrac{1}{2}\)BC \(\times\) AH = \(\dfrac{1}{2}\) \(\times\) \(\dfrac{50}{3}\) \(\times\) 8 = \(\dfrac{200}{3}\) (cm2)
Vì M là trung điểm của tam giác ABC nên
SABM = \(\dfrac{1}{2}\) SABC (hai tam giác có chung chiều cao hạ từ đỉnh A xuống đáy BC và BM = \(\dfrac{1}{2}\) BC)
SABM = \(\dfrac{200}{3}\).\(\dfrac{1}{2}\) = \(\dfrac{100}{3}\) (cm2)
SAHB = \(\dfrac{1}{2}\)AH.HB = \(\dfrac{8.6}{2}\) = 24 (cm2)
SAHB + SAHM = SABM
⇒ SAHM = SABM - SAHB
SAHM = \(\dfrac{100}{3}\) - 24 = \(\dfrac{28}{3}\) (cm2)
Kết luận: BC dài \(\dfrac{50}{3}\) cm; Diện tích tam giác AHM là \(\dfrac{28}{3}\) cm2


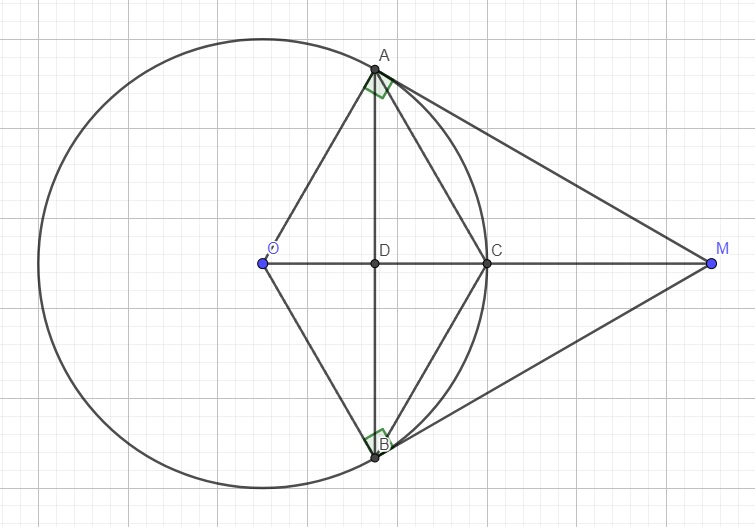


a: Xét tứ giác AOBM có \(\widehat{OAM}+\widehat{OBM}=90^0+90^0=180^0\)
nên AOBM là tứ giác nội tiếp
b: Xét ΔAOM vuông tại A có \(sinAMO=\dfrac{AO}{OM}=\dfrac{1}{2}\)
nên \(\widehat{AMO}=30^0\)
Xét (O) có
MA,MB là các tiếp tuyến
DO đó: MA=MB và MO là phân giác của góc AMB
MO là phân giác của góc AMB
=>\(\widehat{AMB}=2\cdot\widehat{AMO}=60^0\)
AOBM nội tiếp
=>\(\widehat{AOB}+\widehat{AMB}=180^0\)
=>\(\widehat{AOB}=120^0\)
Độ dài đường tròn (O) là:
\(C=2\cdot5\cdot3,14=31,4\left(cm\right)\)
Diện tích hình quạt tròn ứng với cung nhỏ AB là:
\(S_{q\left(AB\right)}=\Omega\cdot5^2\cdot\dfrac{120}{360}=5^2\cdot\dfrac{3.14}{3}=\dfrac{157}{6}\left(cm^2\right)\)
c: Xét (O) có
MA,MB là các tiếp tuyến
Do đó: OM là phân giác của góc AOB
=>\(\widehat{AOM}=\widehat{BOM}=\dfrac{120^0}{2}=60^0\)
Xét ΔOAC có OA=OC và \(\widehat{AOC}=60^0\)
nên ΔOAC đều
=>AC=OC=OA=R
Xét ΔOCB có OC=OB và \(\widehat{COB}=60^0\)
nên ΔOCB đều
=>OC=CB=OB=R
Xét tứ giác OACB có
OA=AC=CB=OB
nên OACB là hình thoi