Help me 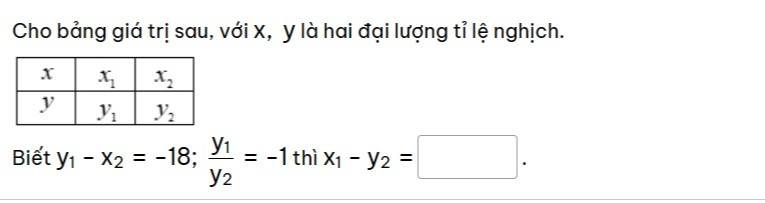
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(x\) tỉ lệ thuận với \(y\) theo hệ số tỉ lệ là 2
\(\Rightarrow x=2y\)
\(y\) tỉ lệ thuận với \(z\) theo hệ số tỉ lệ \(-\dfrac{1}{2}\)
\(\Rightarrow y=\dfrac{-1}{2}.z\)
\(\Rightarrow x=2y=2.\left(-\dfrac{1}{2}.z\right)=-z\)
Khi \(x=5\Rightarrow-z=5\Rightarrow z=-5\)
x tỉ lệ thuận y theo hệ số tỉ lệ \(k=2\Rightarrow x=2y\)
y và z tỉ lệ nghịch theo hệ số tỉ lệ \(k=-\dfrac{1}{2}\Rightarrow yz=-\dfrac{1}{2}\)
Khi \(x=-5\Rightarrow y=\dfrac{x}{2}=-\dfrac{5}{2}\)
\(\Rightarrow\left(-\dfrac{5}{2}\right).z=-\dfrac{1}{2}\)
\(\Rightarrow z=-\dfrac{1}{2}:\left(-\dfrac{5}{2}\right)=\dfrac{1}{5}\)

\(2x\left(3x^2+4x+1\right)\)
\(=2x.3x^2+2x.4x+2x.1\)
\(=6x^3+8x^2+2x\)
------------------
\(\left(2x+1\right)\left(x-2\right)\)
\(=2x\left(x-2\right)+1.\left(x-2\right)\)
\(=2x.x-2x.2+x-2\)
\(=2x^2-4x+x-2\)
\(=2x^2+\left(-4x+x\right)-2\)
\(=2x^2-3x-2\)

a, Thu gọn và sắp xếp đa thức theo lũy thừa giảm dần của biến.
P(\(x\)) = 7\(x^3\) + 4\(x^4\) - 2\(x^2\) + 3\(x^2\) - 3\(x^3\) - \(x^4\) + 5 - 4\(x^3\)
P(\(x\)) = (7\(x^3\) - 3\(x^3\) - 4\(x^3\))+ (4\(x^4\) - \(x^4\)) - (2\(x^2\) - 3\(x^2\)) + 5
P(\(x\)) = 0 + 3\(x^4\) - (-\(x^2\)) +5
P(\(x\)) = 3\(x^4\) + \(x^2\) + 5
b; Hệ số cao nhất là 3; bậc của đa thức là 4; hệ số tự do của đa thức trên là 5

a: Xét ΔBAH vuông tại A và ΔBMH vuông tại M có
BH chung
\(\widehat{ABH}=\widehat{MBH}\)
Do đó: ΔBAH=ΔBMH
b: ΔBAH=ΔBMH
=>BA=BM và HA=HM
Ta có: BA=BM
=>B nằm trên đường trung trực của AM(1)
ta có: HA=HM
=>H nằm trên đường trung trực của AM(2)
Từ (1),(2) suy ra BH là đường trung trực của AM
c: Xét ΔBMN vuông tại M và ΔBAC vuông tại A có
BM=BA
\(\widehat{MBN}\) chung
Do đó: ΔBMN=ΔBAC
=>BN=BC
Xét ΔBNC có \(\dfrac{BA}{BN}=\dfrac{BM}{BC}\)
nên AM//NC
d: Xét ΔBNC có
NM,CA là các đường cao
NM cắt CA tại H
Do đó: H là trực tâm của ΔBNC
=>BH\(\perp\)CN

a: Xét ΔABC có \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)
=>\(\widehat{A}+84^0+48^0=180^0\)
=>\(\widehat{A}+132^0=180^0\)
=>\(\widehat{A}=48^0\)
b: Xét ΔCAB có \(\widehat{BAC}=\widehat{BCA}\left(=48^0\right)\)
nên ΔBAC cân tại B
Do x và y là hai đại lượng tỉ lệ nghịch
\(\Rightarrow\dfrac{y_1}{y_2}=\dfrac{x_2}{x_1}\)
Do \(\dfrac{y_1}{y_2}=-1\Rightarrow\dfrac{x_2}{x_1}=-1\)
\(\Rightarrow x_1=-x_2;y_2=-y_1\)
\(\Rightarrow x_1-y_2=-x_2-\left(-y_1\right)=y_1-x_2=-18\)
Do x;y là 2 đại lượng tỉ lệ nghịch
\(\Rightarrow x_1y_1=x_2y_2\Rightarrow\dfrac{y_1}{y_2}=\dfrac{x_2}{x_1}=\dfrac{y_1-x_2}{y_2-x_1}=-1\)
\(\Rightarrow\dfrac{-18}{y_2-x_1}=-1\Rightarrow y_2-x_1=18\)
\(\Rightarrow x_1-y_2=-18\)