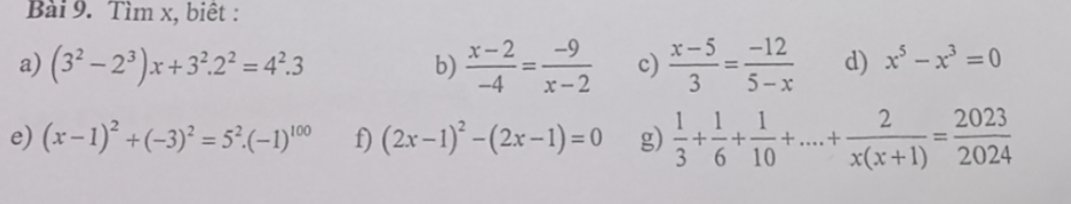\(a)\sqrt{2+\sqrt{3}}-\sqrt{2-\sqrt{3}}\\ =\dfrac{\sqrt{4+2\sqrt{3}}}{\sqrt{2}}-\dfrac{\sqrt{4-2\sqrt{3}}}{\sqrt{2}}\\ =\dfrac{\sqrt{1^2+2\cdot1\cdot\sqrt{3}+\left(\sqrt{3}\right)^2}-\sqrt{\left(\sqrt{3}\right)^2-2\cdot\sqrt{3}\cdot1+1^2}}{\sqrt{2}}\\ =\dfrac{\sqrt{\left(\sqrt{3}+1\right)^2}-\sqrt{\left(\sqrt{3}-1\right)^2}}{\sqrt{2}}\\ =\dfrac{\sqrt{3}+1-\sqrt{3}+1}{\sqrt{2}}\\ =\dfrac{2}{\sqrt{2}}\\ =\sqrt{2}\) 

b) 

\(\sqrt{3+\sqrt{5}}-\sqrt{3-\sqrt{5}}-\sqrt{2}\\ =\dfrac{\sqrt{6+2\sqrt{5}}}{\sqrt{2}}-\dfrac{\sqrt{6-2\sqrt{5}}}{\sqrt{2}}-\sqrt{2}\\ =\dfrac{\sqrt{\left(\sqrt{5}\right)^2+2\cdot\sqrt{5}\cdot1+1^2}}{\sqrt{2}}-\dfrac{\sqrt{\left(\sqrt{5}\right)^2-2\cdot\sqrt{5}\cdot1+1^2}}{\sqrt{2}}-\sqrt{2}\\ =\dfrac{\sqrt{\left(\sqrt{5}+1\right)^2}}{\sqrt{2}}-\dfrac{\sqrt{\left(\sqrt{5}-1\right)^2}}{\sqrt{2}}-\sqrt{2}\\ =\dfrac{\sqrt{5}+1-\sqrt{5}+1-2}{\sqrt{2}}\\ =\dfrac{0}{\sqrt{2}}\\ =0\)

Bài 1:

\(a)8^2\cdot8^3\\ =8^{2+3}\\ =8^5\\ b)12^5:12^2\\ =12^{5-2}\\ =12^3\\ c)7^4:7\\ =7^{4-1}\\ =7^3\\ d)9^{15}\cdot9\\ =9^{15+1}\\ =9^{16}\\ e)64:4^2\\ =4^3:4^2\\=4^{3-2}\\ =4\\ f)216\cdot6^{20}\\ =6^3\cdot6^{20}\\ =6^{3+20}\\ =6^{23}\\ g)64:16\\ =2^6:2^4\\ =2^{6-4}\\ =2^2\\ h)a^2\cdot a^7:a=a^{2+7-1}\\ =a^8\)

Bài 2:

a: \(3^x=81\)

=>\(3^x=3^4\)

=>x=4

b: \(\left(3x-5\right)^2=49\)

=>\(\left[{}\begin{matrix}3x-5=7\\3x-5=-7\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}3x=12\\3x=-2\end{matrix}\right.\)

=>\(\left[{}\begin{matrix}x=4\\x=-\dfrac{2}{3}\end{matrix}\right.\)

c: \(6^{x-5}=36\)

=>\(6^{x-5}=6^2\)

=>x-5=2

=>x=5+2=7

d: \(\left(7-2x\right)^3=27\)

=>7-2x=3

=>2x=7-3=4

=>x=4/2=2

a) 

\(\left(3^2-2^3\right)x+3^2\cdot2^2=4^2\cdot3\\ \left(9-8\right)x+36=48\\ x=48-36\\ x=12\)

b) 

\(\dfrac{x-2}{-4}=\dfrac{-9}{x-2}\left(x\ne2\right)\\\left(x-2\right)^2 =-4\cdot-9\\ \left(x-2\right)^2=36\\ \left(x-2\right)^2=6^2 \)

TH1: x - 2 = 6 

x = 8

TH2: x - 2 = -6

x = -4

c) 

\(\left(x-1\right)^2+\left(-3\right)^2=5^2\cdot\left(-1\right)^{100}\\ \left(x-1\right)^2+9=25\cdot1\\ \left(x-1\right)^2=25-9=16\\ \left(x-1\right)^2=4^2\)

TH1:  x - 1 = 4

x = 5

TH2: x - 1 = -4

x = -3

d) x⁵-x³=0

⇔ x³(x²-1)=0

⇔ x³(x-1)(x+1)=0

TH1: x=0

TH2: x-1=0 ⇔ x =1

TH3: x + 1=0 ⇔ x =-1

c) x-5 / 3 = -12 /5-x

⇔ x-5 / 3  = 12 / x-5 

⇔ (x-5)²= 36

⇔ (x-5)²= 6²

^{TH1: x -5 =6} 

⇔ x = 11

TH2: x- 5 = -6

⇔ x = -1

f)  ⇔ (2x-1)(2x-2)=0

TH1: 2x-1 = 0 

⇔ x = 1/2

TH2: 2x-2 = 0

⇔ x=1

g) bài toán có quy luật

⇔ \(\dfrac{2}{6}+\dfrac{2}{12}+\dfrac{2}{20}+...+\dfrac{2}{x\left(x+1\right)}=\dfrac{2023}{2024}\)   (nhân 2 cả tử và mẫu)

⇔\(\dfrac{1}{6}+\dfrac{1}{12}+\dfrac{1}{20}+...+\dfrac{1}{x\left(x+1\right)}=\dfrac{2023}{4048}\)   ( chia hai vế cho 2 )

⇔\(\dfrac{1}{2.3}+\dfrac{1}{3.4}+\dfrac{1}{4.5}+...+\dfrac{1}{x\left(x+1\right)}=\dfrac{2023}{4048}\)

⇔\(\dfrac{3-2}{2.3}+\dfrac{4-3}{3.4}+\dfrac{5-4}{4.5}+...+\dfrac{\left(x+1\right)-x}{x\left(x+1\right)}=\dfrac{2023}{4048}\) 

⇔\(\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+...+\dfrac{1}{x}-\dfrac{1}{x+1}=\dfrac{2023}{4048}\)

⇔\(\dfrac{1}{2}-\dfrac{1}{x+1}=\dfrac{2023}{4048}\)    ( rút gọn ta đc)

⇔\(\dfrac{\left(x+1\right)-2}{2.\left(x+1\right)}=\dfrac{2023}{4048}\) ( quy đồng)

⇔ \(\dfrac{x-1}{x+1}=\dfrac{2023}{2024}\)    ( nhân 2 vế cho 2 )

⇔ 2024.(x-1)= 2023. ( x+1)

⇔ 2024x -2024 = 2023x + 2023

⇔ 2024x - 2023x= 2023+2024

⇔ x = 4047

tick cho tui nha! 

Chiều rộng của căn phòng là:

 2/3 x 60 = 40 (m)

Diện tích căn phòng là:

 60 x 40 = 2400 (m^2)

Diện tích mỗi viên gạch là:

20 x 20 = 400 (cm^2)

Đổi: 400 cm^2 = 0,04 m^2

Cần phài dùng số viên gạch để lát nền là:

2400 : 0,04 = 60000 (viên)

ĐS: .. 

bạn học đâu vậy

A, B,L,H là tuổi của An, Ba, Lan và Hương

A+B=L+H ⇒A-H=L-B

mà A>H ⇒ A-H>0 ⇒L-B>0 ⇒L>B
Vậy Lan già hơn Ba

Ba và An bằng tuổi lan và Hương nên An hơn Hương bao nhiêu tuổi thì An kém Lan bấy nhiêu tuổi. 

\(1+3+5+...+101\)

Số số hạng của dãy \(1+3+5+...+101\) là:

\(\left(101-1\right):2+1=51\) (số hạng)

Tổng dãy \(1+3+5+...+101\) là :

\(\left(101+1\right)\times51:2=2601\)

Đáp số : \(2601\)

Số số hạng của tổng là:

\(\left(101-1\right):2+1=51\) (số)

Giá trị của tổng là:

\(1+3+5+...+101=\left(101+1\right)\cdot51:2=2601\)

\(\left(\dfrac{2}{7}-\dfrac{9}{4}\right)-\left(-\dfrac{3}{7}+\dfrac{5}{4}\right)-\left(\dfrac{2}{4}-\dfrac{9}{7}\right)\)

\(=\dfrac{2}{7}-\dfrac{9}{4}+\dfrac{3}{7}-\dfrac{5}{4}-\dfrac{2}{4}+\dfrac{9}{7}\)

\(=\left(\dfrac{2}{7}+\dfrac{3}{7}+\dfrac{9}{7}\right)-\left(\dfrac{9}{4}+\dfrac{5}{4}+\dfrac{2}{4}\right)\)

\(=2-4\)

\(=-2\)

-2

Quãng đường Nam đi được trong 3 giờ đầu là:

\(12\cdot3=36\left(km\right)\)

Quãng đường Nam đi được trong 2 giờ sau là:

\(11\cdot2=22\left(km\right)\)

Quãng đường Nam đi được trong 5 giờ là:

\(36+22=58\left(km\right)\)

Vậy...

Tổng quãng đường mà bạn Nam đi được trong 3 giờ đầu là:

\(3\times12=36\left(km\right)\)

Tổng quãng đường mà bạn Nam đi được trong 2 giờ sau là:

\(2\times11=22\left(km\right)\)

Tổng quãng đường mà bạn Nam đi được trong 5 giờ là:

\(36+22=58\left(km\right)\)

Đáp số : \(58km\)

Số gà và vịt sau khi bán là:

\(145-13-22=110\) (con)

Số vịt sau khi bán là:

\(110:\left(2+3\right)\times3=66\) (con)

Số vịt trước khi bán là:

\(66+22=88\) (con)

Đ/s:...

tổng số gà và vịt còn lại là: 145-13-22 = 110

số vịt còn lại: 110:(2+3)x3=66

số vịt lúc chưa bán: 66+22=88