Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương trình hoành độ giao điểm:
\(-x^2=2mx-3m+4\Leftrightarrow x^2+2mx-3m+4=0\) (1)
(P) tiếp xúc (d) khi và chỉ khi (1) có nghiệm kép
\(\Leftrightarrow\Delta'=m^2-\left(-3m+4\right)=0\Leftrightarrow m^2+3m-4=0\)
\(\Rightarrow\left[{}\begin{matrix}m=1\\m=-4\end{matrix}\right.\)
Với \(m=1\Rightarrow x_{1,2}=-\dfrac{2m}{2}=-m=-1\)
Với \(m=-4\Rightarrow x_{1,2}=-m=4\)


\(P=\dfrac{x\sqrt{2}}{2\sqrt{x}+x\sqrt{2}}+\dfrac{\sqrt{2x}-2}{x-2}=\dfrac{x\sqrt{2}}{\sqrt{2x}\left(\sqrt{2}+\sqrt{x}\right)}+\dfrac{\sqrt{2}\left(\sqrt{x}-\sqrt{2}\right)}{\left(\sqrt{x}-\sqrt{2}\right)\left(\sqrt{x}+\sqrt{2}\right)}\)
\(=\dfrac{\sqrt{x}}{\sqrt{x}+\sqrt{2}}+\dfrac{\sqrt{2}}{\sqrt{x}+\sqrt{2}}=\dfrac{\sqrt{x}+\sqrt{2}}{\sqrt{x}+\sqrt{2}}=1\)

\(\sqrt{4x^2+xy+4y^2}=\sqrt{\dfrac{7}{2}\left(x^2+y^2\right)+\dfrac{1}{2}\left(x^2+2xy+y^2\right)}\ge\sqrt{\dfrac{7}{4}\left(x+y\right)^2+\dfrac{1}{2}\left(x+y\right)^2}=\dfrac{3}{2}\left(x+y\right)\)
Tương tự:
\(\sqrt{4y^2+yz+4z^2}\ge\dfrac{3}{2}\left(y+z\right)\); \(\sqrt{4z^2+zx+4x^2}\ge\dfrac{3}{2}\left(z+x\right)\)
Cộng vế:
\(B\ge\dfrac{3}{2}\left(x+y+y+z+z+x\right)=3\left(x+y+z\right)\)
\(B\ge3.\dfrac{1}{3}\left(\sqrt{x}+\sqrt{y}+\sqrt{z}\right)^2=1\)
\(B_{min}=1\) khi \(x=y=z=\dfrac{1}{9}\)

\(\left(1-\frac{x}{x-\sqrt{x}+1}\right):\frac{x+2\sqrt{x}+1}{x\sqrt{x}+1}\)
\(=\frac{x-\sqrt{x}+1-x}{x-\sqrt{x}+1}.\frac{\left(\sqrt{x}\right)^3+1}{\left(\sqrt{x}+1\right)^2}\)
\(=\frac{1-\sqrt{x}}{x-\sqrt{x}+1}.\frac{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)^2}\)
\(=\frac{1-\sqrt{x}}{\sqrt{x}+1}\)

\(a,P=\frac{3x+3\sqrt{x}-3}{x+\sqrt{x}-2}+\frac{1}{\sqrt{x}-1}+\frac{1}{\sqrt{x}+2}-2\)
\(P=\frac{3x+3\sqrt{x}-3+\sqrt{x}+2+\sqrt{x}-1-2x-2\sqrt{x}+4}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}\)
\(P=\frac{x+3\sqrt{x}+2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}=\frac{\left(\sqrt{x}+1\right)\left(\sqrt{x}+2\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}=\frac{\sqrt{x}+1}{\sqrt{x}-1}\)
\(b,P=\frac{\sqrt{x}+1}{\sqrt{x}-1}=\frac{\sqrt{x}-1+2}{\sqrt{x}-1}=1+\frac{2}{\sqrt{x}-1}\)
\(\sqrt{x}-1\ge-1\)
\(\Leftrightarrow\frac{2}{\sqrt{x}-1}\le-2\)
\(\Leftrightarrow P\le1-2=-1\)
\(c,P=4\)\(\Leftrightarrow\sqrt{x}+1=4\sqrt{x}-4\Leftrightarrow3\sqrt{x}=5\Leftrightarrow x=\frac{25}{9}\)
d, Do câu b, \(P\le-1\)\(\Rightarrow P< -3\)
 giúp mik với nhé ^^
giúp mik với nhé ^^
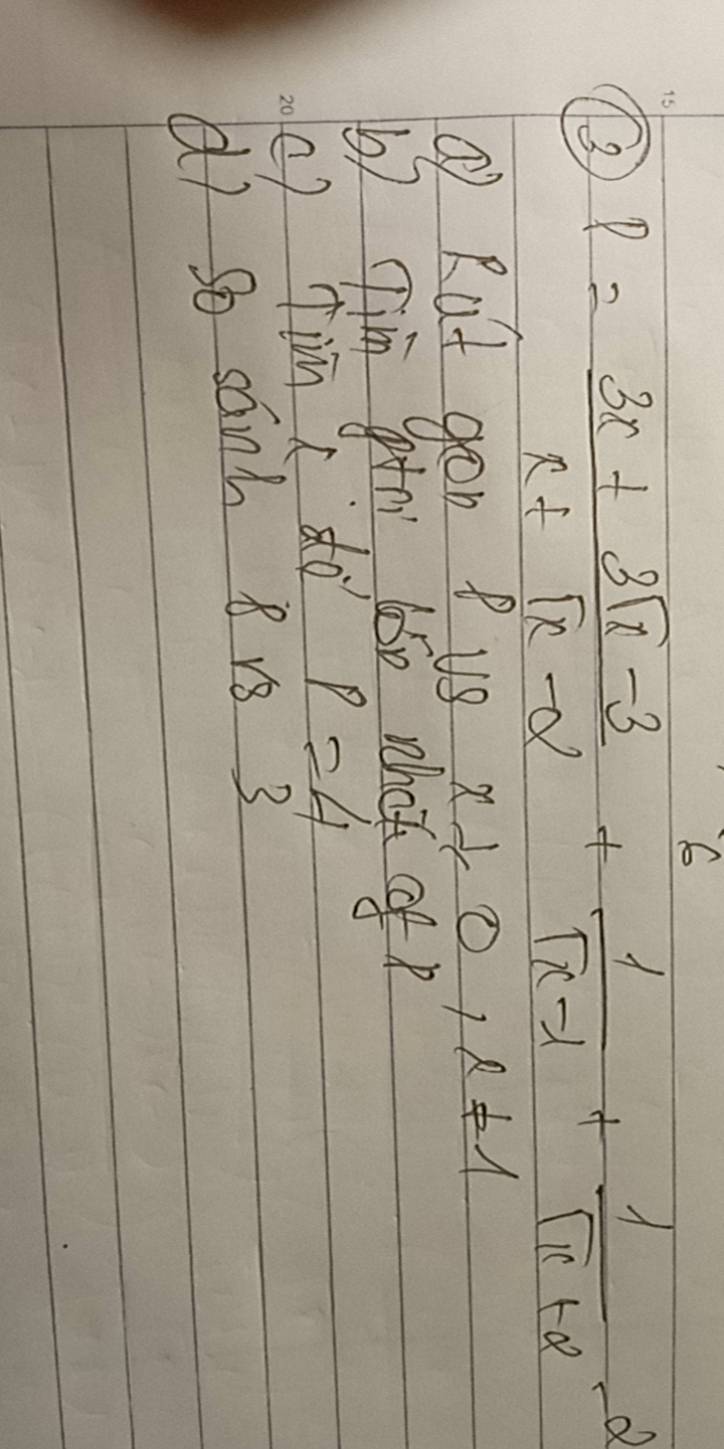
Hai tam giác AEF và ABF có chung đường cao hạ từ F nên ta có \(\frac{S_{AEF}}{S_{ABF}}=\frac{AE}{AB}=\frac{4}{6}=\frac{2}{3}\)(1)
Hai tam giác ABF và ABC có chung đường cao hạ từ B nên ta có \(\frac{S_{ABF}}{S_{ABC}}=\frac{AF}{AC}=\frac{4}{9}\)(2)
Từ (1) và (2) \(\Rightarrow\frac{S_{AEF}}{S_{ABF}}.\frac{S_{ABF}}{S_{ABC}}=\frac{2}{3}.\frac{4}{9}\)\(\Rightarrow\frac{S_{AEF}}{S_{ABC}}=\frac{8}{27}\)\(\Rightarrow S_{AEF}=\frac{8}{27}S_{ABC}=\frac{8}{27}.27=8\left(cm^2\right)\)
Vậy \(S_{AEF}=8cm^2\)
Bạn vào thống kê hỏi đáp của mình xem câu trả lời nhé. Nó chưa duyệt lên.