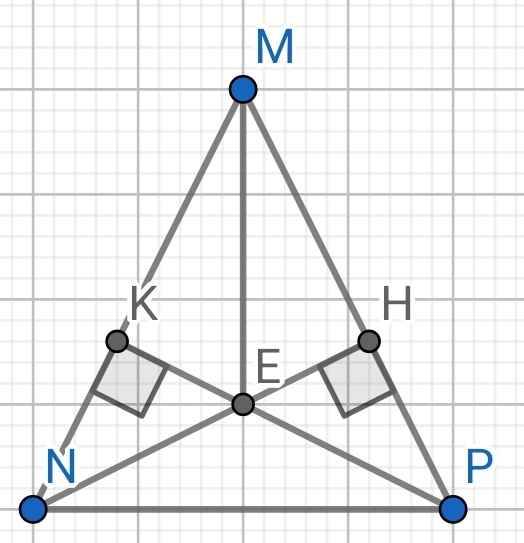
a) Do ∆MNP cân tại M (gt)

⇒ ∠MPN = ∠MNP

⇒ ∠HPN = ∠KNP

Xét hai tam giác vuông: ∆NHP và ∆PKN có:

NP là cạnh chung

∠HPN = ∠KNP (cmt)

⇒ ∆NHP = ∆PKN (cạnh huyền - góc nhọn)

b) Do ∆NHP = ∆PKN (cmt)

⇒ ∠HNP = ∠KPN (hai góc tương ứng)

⇒ ∠ENP = ∠EPN

∆ENP có:

∠ENO = ∠EPN (cmt)

⇒ ∆ENP cân tại E

c) ∆MNP có hai đường cao NH và PK cắt nhau tại E

⇒ ME là đường cao thứ ba của ∆MNP

Mà ∆MNP cân tại M (gt)

⇒ ME vừa là đường cao cũng vừa là đường phân giác của ∆MNP

⇒ ME là tia phân giác của ∠NMP

Câu 16:

a: Xét ΔBAH và ΔBDH có

BA=BD

AH=DH

BH chung

Do đó: ΔBAH=ΔBDH

b: ΔBAH=ΔBDH

=>\(\widehat{ABH}=\widehat{DBH}\)

Xét ΔBAE và ΔBDE có

BA=BD

\(\widehat{ABE}=\widehat{DBE}\)

BE chung

Do đó: ΔBAE=ΔBDE

=>EA=ED
=>ΔEAD cân tại E

c: ta có: ED=EA

mà EA<EM(ΔEAM vuông tại A)

nên ED<EM

Câu 13:

a: Đặt P(x)=0

=>x-5=0

=>x=5

Đặt M(x)=0

=>2x+4=0

=>2x=-4

=>x=-2

b: \(A\left(-3\right)=2\cdot\left(-3\right)+6=-6+6=0\)

=>x=-3 là nghiệm của A(x)

c: B(2)=-6

=>\(a\cdot2+4=-6\)

=>2a=-10

=>a=-5

If fossil fuels run out, they will take millions of years to form.

TK:

Để chứng minh rằng \( BE \) vuông góc với \( AC \), ta sẽ sử dụng các định lí về tam giác vuông và tính chất của phân giác trong tam giác.

Vì tam giác \( ABC \) vuông tại \( A \), nên phân giác \( BE \) sẽ chia góc \( CAB \) thành hai góc nhỏ bằng nhau, tức là \( \angle BAE = \angle CAE \).

Vì \( EH \) là đường cao của tam giác \( BEC \), nên \( EH \) vuông góc với \( BC \).

Xét tam giác \( BEH \) và \( CEA \):
- \( \angle BEH = \angle CEA \) (vì cùng là góc phân giác)
- \( \angle EHB = \angle EAC \) (vì \( EH \) song song với \( AC \))
- \( EH \) vuông góc với \( BC \) và \( AC \) (do phân giác chia góc \( CAB \))
=> \( BE \) là đường cao của tam giác \( BEC \) (theo tính chất của tam giác vuông).
=> \( BE \) vuông góc với \( AC \), vì đường cao luôn vuông góc với đáy của tam giác.

Vậy, ta đã chứng minh được rằng \( BE \) vuông góc với \( AC \).

Sửa đề; Chứng minh BE\(\perp\)KC

Xét ΔBKC có

CA,KH là các đường cao

CA cắt KH tại E

Do đó: E là trực tâm của ΔBKC

=>BE\(\perp\)KC

a) Việc làm của bạn Tuấn trong tình huống trên là sai.

b) Nếu em là bạn của Tuấn trong trường hợp đó, em sẽ khuyên bạn không nên làm như vậy, giải thích cho bạn hiểu, nói những tác hại của những việc làm đó và thuyết phục bạn để bạn hiểu và tỉnh ngộ.

TK:

a. Về việc làm của Tuấn trong tình huống trên, có một số nhận xét sau:
- Tuấn đã bắt đầu từ việc nói dối và lừa dối mẹ để có tiền đi chơi điện tử, đây là dấu hiệu của hành vi không trung thực và không tôn trọng người khác.
- Việc Tuấn quen nhiều bạn bè và rủ rê vào các hành vi xấu như ăn chơi, đua đòi và thường xuyên nghỉ học cho thấy sự mất kiểm soát và không ý thức về trách nhiệm của một học sinh.
- Hành vi thử ma túy và sau đó nghiện là một hành động nguy hiểm và đầy hậu quả. Nghiện ma túy không chỉ ảnh hưởng đến sức khỏe mà còn gây ra các hành vi phạm tội và tội ác khác.
- Việc lấy trộm xe máy và tham gia cướp giật tài sản là hành vi phạm pháp nghiêm trọng, ảnh hưởng đến an ninh và trật tự công cộng.

b. Nếu em là bạn của Tuấn trong trường hợp đó, em sẽ:
- Cố gắng thuyết phục Tuấn hiểu được hậu quả của hành vi của mình và thúc đẩy anh ta tìm kiếm sự giúp đỡ từ người thân, bạn bè hoặc cơ quan chức năng.
- Khuyến khích Tuấn tham gia vào các hoạt động tích cực và xây dựng, như các hoạt động văn hóa, thể thao hoặc các khóa huấn luyện kỹ năng sống.
- Báo cáo về tình trạng của Tuấn cho người thân hoặc giáo viên, nhằm giúp anh ta nhận ra và thực hiện các biện pháp cần thiết để cải thiện tình hình của mình.

A(x)+B(x)= x^3 + 2x^2 -x+1+2x^3 +3x^2 +4x +5

= ( x^3 +2x^3) + ( 2x^2 + 3x^2) + ( -x +4x ) + ( 1 +5) 

= 3x^3 + 5x^2 + 3x +6

A(x) - B(x) = x^3 +2x^2 -x+1 - 2x^3 - 3x^2 -4x-5

= (x^3 - 2x^3) + ( 2x^2 - 3x^2) + ( -x -4x ) + ( 1-5)

= -x^3 - x^2 - 5x-4

 Đây nha bạn :)

a: Xét ΔAIB và ΔAIC có

AI chung

IB=IC

AB=AC

Do đó: ΔAIB=ΔAIC

b: ΔABC cân tại A

=>\(\widehat{ABC}=\widehat{ACB}\)(hai góc ở đáy)

TK:

- Đẻ trứng: thực chất là đẻ trứng nhưng trứng được giữ lại trong cơ thể mẹ đến khi nở ra con mới sinh ra ngoài, vì vậy trứng được bảo vệ tốt hơn. Phôi thai vẫn phát triển nhờ chất dinh dưỡng có trong noãn hoàng.
- Đẻ con: Phôi thai phát triển tốt hơn nhờ chất dinh dưỡng lấy từ cơ thể mẹ qua nhau thai. Thai cũng được bảo vệ tốt hơn trong suốt thời gian phát triển. (Ở những loài đẻ con, số lượng con thường ít).

TK:

- Đẻ trứng: thực chất là đẻ trứng nhưng trứng được giữ lại trong cơ thể mẹ đến khi nở ra con mới sinh ra ngoài, vì vậy trứng được bảo vệ tốt hơn. Phôi thai vẫn phát triển nhờ chất dinh dưỡng có trong noãn hoàng.
- Đẻ con: Phôi thai phát triển tốt hơn nhờ chất dinh dưỡng lấy từ cơ thể mẹ qua nhau thai. Thai cũng được bảo vệ tốt hơn trong suốt thời gian phát triển. (Ở những loài đẻ con, số lượng con thường ít).

Bài 1:

a: \(A\left(x\right)=2x^4+3x^2-x+3-x^2-x^4-6x^3\)

\(=\left(2x^4-x^4\right)-6x^3+\left(3x^2-x^2\right)-x+3\)

\(=x^4-6x^3+2x^2-x+3\)

\(B\left(x\right)=10x^3+3-x^4-4x^3+4x-2x^2\)

\(=-x^4+\left(10x^3-4x^3\right)-2x^2+4x+3\)

\(=-x^4+6x^3-2x^2+4x+3\)

b: M(x)=A(x)+B(x)

\(=x^4-6x^3+2x^2-x+3-x^4+6x^3-2x^2+4x+3\)

=3x+6

N(x)=A(x)-B(x)

\(=x^4-6x^3+2x^2-x+3+x^4-6x^3+2x^2-4x-3\)

\(=2x^4-12x^3+4x^2-5x\)

c: M(x)=0

=>3x+6=0

=>3x=-6

=>x=-2

Bài 3: 

a: \(A\left(x\right)=x-5x^3-2x^2+9x^3-\left(x-1\right)-2x^2\)

\(=\left(-5x^3+9x^3\right)+\left(-2x^2-2x^2\right)+\left(x-x\right)+1\)

\(=4x^3-4x^2+1\)

\(B\left(x\right)=-4x^3-2\left(x^2+1\right)+6x+2x^2-9x+2x^3\)

\(=\left(-4x^3+2x^3\right)+\left(-2x^2+2x^2\right)+6x-9x-2\)

\(=-2x^3-3x-2\)

\(C\left(x\right)=2x-6x^2-4+x^3\)

\(=x^3-6x^2+2x-4\)

b: M(x)=A(x)+B(x)-C(x)

\(=4x^3-4x^2+1-2x^3-3x-2-x^3+6x^2-2x+4\)

\(=x^3+2x^2-5x+3\)

c: \(P\left(x\right)=3\cdot M\left(x\right)-3x^3-9\)

\(=3x^3+6x^2-15x+9-3x^3-9=6x^2-15x\)

Đặt P(x)=0

=>\(6x^2-15x=0\)

=>\(2x^2-5x=0\)

=>x(2x-5)=0

=>\(\left[{}\begin{matrix}x=0\\x=\dfrac{5}{2}\end{matrix}\right.\)

Câu 3: 

a: Xét ΔACE vuông tại A và ΔKCE vuông tại K có

CE chung

\(\widehat{ACE}=\widehat{KCE}\)

Do đó: ΔACE=ΔKCE

=>CA=CK và EA=EK

Ta có: CA=CK

=>C nằm trên đường trung trực của AK(1)

Ta có: EA=EK

=>E nằm trên đường trung trực của AK(2)

Từ (1),(2) suy ra CE là đường trung trực của AK

=>CE\(\perp\)AK

b: Xét ΔABC vuông tại A có \(cosACB=\dfrac{AC}{BC}\)

=>\(\dfrac{AC}{BC}=cos60=\dfrac{1}{2}\)

=>BC=2AC

Xét ΔABC vuông tại A có \(\widehat{ABC}+\widehat{ACB}=90^0\)

=>\(\widehat{ABC}=90^0-60^0=30^0\)

CE là phân giác của góc ACB

=>\(\widehat{ACE}=\widehat{BCE}=\dfrac{\widehat{ACB}}{2}=30^0\)

Xét ΔEBC có \(\widehat{EBC}=\widehat{ECB}\left(=30^0\right)\)

nên ΔEBC cân tại E

=>EB=EC

mà EC>AC(ΔEAC vuông tại A)

nên EB>AC

c: Gọi H là giao điểm của BD với CA

Xét ΔCHB có

CD,BA là các đường cao

CD cắt BA tại E

Do đó: E là trực tâm của ΔCHB

=>HE\(\perp\)CB

mà EK\(\perp\)CB

nên H,E,K thẳng hàng

=>CA,EK,BD đồng quy

Bài 4:

a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có

BD chung

\(\widehat{ABD}=\widehat{EBD}\)

Do đó: ΔBAD=ΔBED

=>BA=BE

b: Xét ΔABC có AB<AC

mà \(\widehat{ACB};\widehat{ABC}\) lần lượt là góc đối diện của các cạnh AB,AC

nên \(\widehat{ACB}< \widehat{ABC}\)

mà \(\widehat{ACB}=\widehat{AMD}\left(=90^0-\widehat{ABC}\right);\widehat{ABC}=\widehat{ADM}\left(=90^0-\widehat{BME}\right)\)

nên \(\widehat{AMD}< \widehat{ADM}< \widehat{DAM}\)

=>AD<AM<DM

c: Xét ΔDAM vuông tại A và ΔDEC vuông tại E có

DA=DE

\(\widehat{ADM}=\widehat{EDC}\)(hai góc đối đỉnh)

Do đó: ΔDAM=ΔDEC

=>DM=DC

=>D nằm trên đường trung trực của MC(1)

ta có: BA+AM=BM

BE+EC=BC

mà BA=BE và AM=EC(ΔDAM=ΔDEC)

nên BM=BC

=>B nằm trên đường trung trực của MC(2)

Ta có: KM=KC

=>K nằm trên đường trung trực của MC(3)

từ (1),(2),(3) suy ra B,D,K thẳng hàng