`P=(x-1)+(y-3)z4`

`=x-1+4yz - 12z`

X - 1/2 y đóng ngoặc mũ 2 là

\(2x^2+x+1=2\left(x^2+\dfrac{1}{2}x+\dfrac{1}{16}\right)+\dfrac{7}{8}=2\left(x+\dfrac{1}{4}\right)^2+\dfrac{7}{8}\ge\dfrac{7}{8}>0;\forall x\)

= ( x² + x + \(\dfrac{1}{4}\)) + x² + \(\dfrac{3}{4}\)

= (x+1/2) ² + x² + 3/4

biểu thức trên luôn lớn hơn 0 với ∀x

\(a+b+c=0\Rightarrow a+b=-c\)

\(\Rightarrow\left(a+b\right)^3=\left(-c\right)^3\)

\(\Rightarrow a^3+b^3+3ab\left(a+b\right)=-c^3\)

\(\Rightarrow a^3+b^3+3ab\left(-c\right)=-c^3\) (do \(a+b+c=0\Rightarrow a+b=-c\))

\(\Rightarrow a^3+b^3+c^3=3abc\)

(a+b+c)³=a³+b³+c³+3(a+b)(b+c)(a+c) (1)

Ta có

a+b+c=0(2)

=>(a+b)=-c (3)

(b+c)=-a (4)

(a+c)=-b (5)

Thay (2) (3) (4) (5) vào (1)

0=a³+b³+c³=3(-c)(-a)(-b)

=> a³+b³+c³=3abc (đpcm)

\(P=\dfrac{a^3+b^3+3ab\left(a+b\right)-3ab\left(a+b\right)+c^3}{a^2+b^2+c^2-ab-bc-ca}=\dfrac{\left(a+b\right)^3+c^3-3ab\left(a+b+c\right)}{a^2+b^2+c^2-ab-bc-ca}\)

\(=\dfrac{\left(a+b+c\right)\left[\left(a+b\right)^2-\left(a+b\right)c+c^2\right]-3ab\left(a+b+c\right)}{a^2+b^2+c^2-ab-bc-ca}\)

\(=\dfrac{\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ca\right)}{a^2+b^2+c^2-ab-bc-ca}\)

\(=a+b+c=2022\)

\(3x^2-4xy+2y^2=3\)

\(\Leftrightarrow x^2+2\left(x-y\right)^2=3\)

\(\Rightarrow x^2\le3\Rightarrow\left[{}\begin{matrix}x^2=0\\x^2=1\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=0\Rightarrow y^2=\dfrac{3}{2}\left(ktm\right)\\x=-1\Rightarrow2y^2+4y=0\Rightarrow y=\left\{-2;0\right\}\\x=1\Rightarrow2y^2-4y=0\Rightarrow y=\left\{0;2\right\}\end{matrix}\right.\)

\(\Rightarrow M=...\)

a) △ABC cân ⇒ trung tuyến AH đồng thời là đg cao, đg phân giác

→ AH \(\perp\)BC 

xét △ vuông AHC có HM là đường trung tuyến (do CM là trung tuyến tgiac ABC → M là trung điểm của AB) 

⇒ HM = 1/2 AB = 1/2AC = 5

b) xét tứ giác AGBN có AB và GN cắt nhau tại trung điểm M của mỗi đường

⇒ AGBN là hbh

C) câu này mình chua nghi ra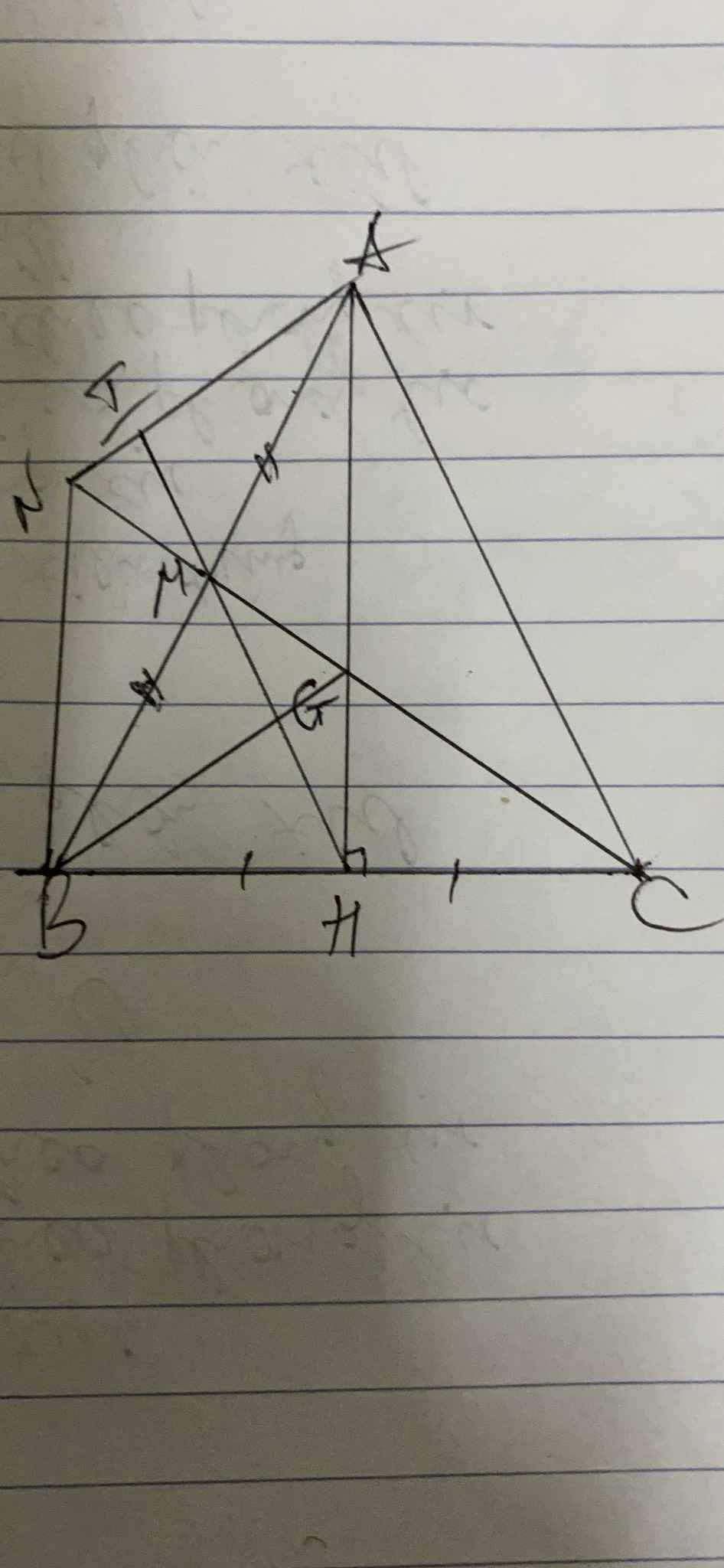 

\(M=\left(x^2-2xy+y^2\right)+\left(9x^2-6x+1\right)=\left(x-y\right)^2+\left(3x-1\right)^2\ge0\)

\(M_{min}=0\) khi \(x=y=\dfrac{1}{3}\)

a/

\(BC=\sqrt{AB^2+AC^2}\) (Pitago)

\(\Rightarrow BC=\sqrt{6^2+8^2}=10cm\)

\(IB=IC\Rightarrow AI=\dfrac{BC}{2}\) (trong tg vuông trung tuyến thuộc cạnh huyền bằng nửa cạnh huyền)

\(\Rightarrow AI=\dfrac{BC}{2}=\dfrac{10}{2}=5cm\)

b/

Ta có

OA=OC (gt)

OI=ON (gt)

=> AICN là hình bình hành (Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường) (1)

\(AI=IC=\dfrac{BC}{2}\) (2)

Từ (1) và (2)

=> AICN là hình thoi (Hình bình hành có hai cạnh liền kề bằng nhau)

Không đủ dữ kiện để c/m AICN là HCN