\(x\left(x-5\right)+3\left(x-5\right)=0\\ \Leftrightarrow\left(x-5\right)\left(x+3\right)=0\\ \Rightarrow\left[{}\begin{matrix}x-5=0\\x+3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=5\\x=-3\end{matrix}\right.\)

Vậy tập nghiệm pt là: \(S=\left\{5;-3\right\}\)

x(x-5)+3(x-5)=0

=>(x-5)(x+3)=0

=>\(\left[{}\begin{matrix}x-5=0\\x+3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=5\\x=-3\end{matrix}\right.\)

a: \(\dfrac{1}{4003}>0;0>-\dfrac{75}{106}\)

Do đó: \(\dfrac{1}{4003}>-\dfrac{75}{106}\)

b: \(-19< -17\)

=>\(-\dfrac{19}{31}< -\dfrac{17}{31}\)

c: \(\dfrac{-33}{37}>\dfrac{-34}{37}\)

mà \(-\dfrac{34}{37}>-\dfrac{34}{35}\)

nên \(\dfrac{-33}{37}>-\dfrac{34}{35}\)

d: \(\dfrac{-13}{77}=\dfrac{-13\cdot205}{77\cdot205}=\dfrac{-2665}{77\cdot205}\)

\(\dfrac{-34}{205}=\dfrac{-34\cdot77}{205\cdot77}=\dfrac{-2618}{205\cdot77}\)

mà -2665<-2618

nên \(\dfrac{-13}{77}< \dfrac{-34}{205}\)

e: \(\dfrac{-456}{461}=-1+\dfrac{5}{461};\dfrac{-123}{128}=-1+\dfrac{5}{128}\)

461>128

=>\(\dfrac{5}{461}< \dfrac{5}{128}\)

=>\(\dfrac{5}{461}-1< \dfrac{5}{128}-1\)

=>\(\dfrac{-456}{461}< \dfrac{-123}{128}\)

\(2x^3+10x^2=0\)

=>\(2x^2\left(x+5\right)=0\)

=>\(x^2\left(x+5\right)=0\)(Vì 2>0)

=>\(\left[{}\begin{matrix}x^2=0\\x+5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-5\end{matrix}\right.\)

\(2x^3+10x^2=0\Leftrightarrow x^2\left(2x+10\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-5\end{matrix}\right.\)

15x8+6x15-15x4

=15x(8+6-4)

=15x10=150

15 x 8 + 6 x15 - 15 x 4

= 15 x (8 + 6 - 4)

= 15 x (14 - 4)

= 15 x 10

= 150

`x^2-6x=0`

`<=>x(x-6)=0`

TH1: `x =0 `

TH2: `x - 6=0<=>x=6`

Vậy: ... 

\(x^2-6x=0\Leftrightarrow x\left(x-6\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=6\end{matrix}\right.\)

a: A={x∈N|x=3k+1; k∈N; 0<=k<=6}

b: B={x∈N|x=k³; 1<=k<=5}

a)Mỗi phần tử đều cách nhau 3 đơn vị

b)ko biết làm

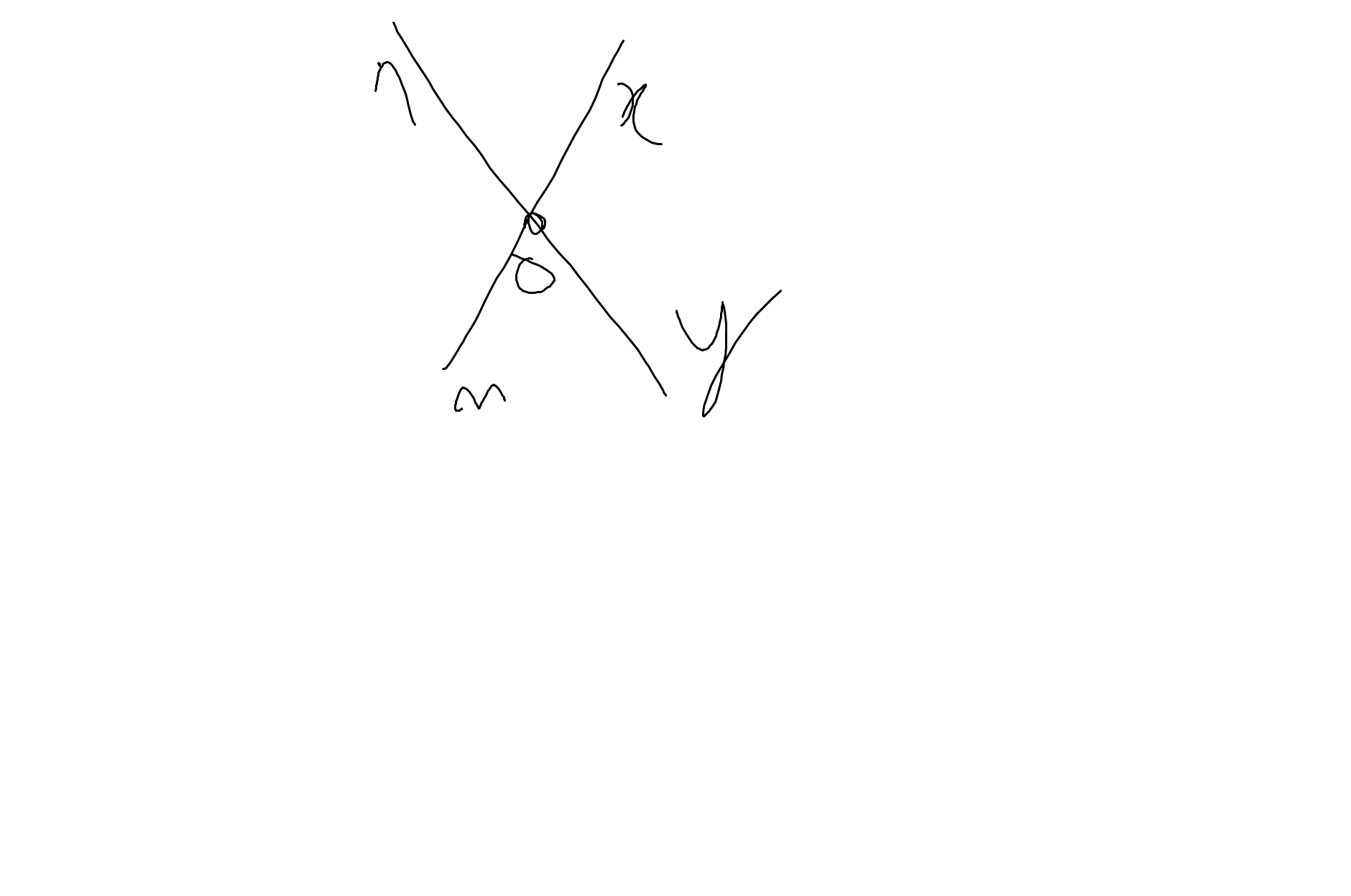
\(\widehat{mOn}=\widehat{xOy}\)(hai góc đối đỉnh)

mà \(\widehat{xOy}=85^0\)

nên \(\widehat{mOn}=85^0\)

Ta có: \(\widehat{nOm}+\widehat{xOn}=180^0\)(hai góc kề bù)

=>\(\widehat{xOn}+85^0=180^0\)

=>\(\widehat{xOn}=180^0-85^0=95^0\)

Ta có: \(\widehat{xOn}=\widehat{yOm}\)(hai góc đối đỉnh)

mà \(\widehat{xOn}=95^0\)

nên \(\widehat{yOm}=95^0\)

\(a)\dfrac{7}{x+4}-\dfrac{3x}{x^2-16}\left(x\ne\pm4\right)\\ =\dfrac{7}{x+4}-\dfrac{3x}{\left(x+4\right)\left(x-4\right)}\\ =\dfrac{7\left(x-4\right)}{\left(x+4\right)\left(x-4\right)}-\dfrac{3x}{\left(x+4\right)\left(x-4\right)}\\ =\dfrac{7x-28-3x}{\left(x+4\right)\left(x-4\right)}\\ =\dfrac{4x-28}{\left(x+4\right)\left(x-4\right)}\\ =\dfrac{4x-28}{x^2-16}\)

\(b)\dfrac{x^2-3}{\left(x-1\right)\left(x-2\right)}-\dfrac{x+1}{x-1}\left(x\ne1;x\ne2\right)\\ =\dfrac{x^2-3}{\left(x-1\right)\left(x-2\right)}-\dfrac{\left(x+1\right)\left(x-2\right)}{\left(x-1\right)\left(x-2\right)}\\ =\dfrac{x^2-3-\left(x^2-2x+x-2\right)}{\left(x-1\right)\left(x-2\right)}\\ =\dfrac{x^2-3-x^2+x+2}{\left(x-1\right)\left(x-2\right)}\\ =\dfrac{x-1}{\left(x-1\right)\left(x-2\right)}\\ =\dfrac{1}{x-2}\) 

\(c)\dfrac{x-3}{x^2-3x+2}+\dfrac{3}{x-2}\left(x\ne1;x\ne2\right)\\ =\dfrac{x-3}{\left(x-1\right)\left(x-2\right)}+\dfrac{3}{x-2}\\ =\dfrac{x-3}{\left(x-1\right)\left(x-2\right)}+\dfrac{3\left(x-1\right)}{\left(x-1\right)\left(x-2\right)}\\ =\dfrac{x-3+3x-3}{\left(x-1\right)\left(x-2\right)}\\ =\dfrac{4x-6}{\left(x-1\right)\left(x-2\right)}\)

a: ĐKXĐ: \(x\notin\left\{-4;4\right\}\)

\(\dfrac{7}{x+4}-\dfrac{3x}{x^2-16}\)

\(=\dfrac{7}{x+4}-\dfrac{3x}{\left(x-4\right)\left(x+4\right)}\)

\(=\dfrac{7\left(x-4\right)-3x}{\left(x+4\right)\left(x-4\right)}=\dfrac{4x-28}{\left(x+4\right)\left(x-4\right)}\)

b: ĐKXĐ: \(x\notin\left\{2;1\right\}\)

\(\dfrac{x^2-3}{\left(x-1\right)\left(x-2\right)}+\dfrac{x+1}{x-1}\)

\(=\dfrac{x^2-3+\left(x+1\right)\left(x-2\right)}{\left(x-1\right)\left(x-2\right)}\)

\(=\dfrac{x^2-3+x^2-x-2}{\left(x-1\right)\left(x-2\right)}=\dfrac{2x^2-x-5}{\left(x-1\right)\left(x-2\right)}\)

c: ĐKXĐ: \(x\notin\left\{1;2\right\}\)

\(\dfrac{x-3}{x^2-3x+2}+\dfrac{3}{x-2}\)

\(=\dfrac{x-3}{\left(x-1\right)\left(x-2\right)}+\dfrac{3}{x-2}\)

\(=\dfrac{x-3+3\left(x-1\right)}{\left(x-1\right)\left(x-2\right)}=\dfrac{4x-6}{\left(x-1\right)\left(x-2\right)}\)

Để viết các số theo yêu cầu, bạn chỉ cần ghép các giá trị số học tương ứng:

a. Mười nghìn, năm chục, một đơn vị:

- Mười nghìn: 10000
- Năm chục: 50
- Một đơn vị: 1

Số đó là: 10000 + 50 + 1 = 10051

b. Năm mười nghìn, năm chục, một đơn vị:

- Năm mười nghìn: 50000
- Năm chục: 50
- Một đơn vị: 1

Số đó là: 50000 + 50 + 1 = 50051

a. 10 051.

b. 50 051.

đề là rút gọn đk bn 

a,đk x khác 3 

 \(\dfrac{2}{x-3}-\dfrac{x-1}{x-3}=\dfrac{2-x+1}{x-3}=\dfrac{3-x}{x-3}=-1\)đ

b,đk x khác -1/2

 \(\dfrac{x-4}{2x+1}+\dfrac{3x-3}{2x+1}=\dfrac{x-4+3x-3}{2x+1}=\dfrac{4x-7}{2x+1}\)

c, đk x khác -4;4 

\(\dfrac{7}{x+4}-\dfrac{3x}{x^2-16}=\dfrac{7\left(x-4\right)-3x}{x^2-16}=\dfrac{7x-28-3x}{x^2-16}=\dfrac{4x-28}{x^2-16}\)

d, đk x khác -1 

\(\dfrac{3x-3}{2x+2}-\dfrac{6}{x+1}=\dfrac{3x-3-12}{2\left(x+1\right)}=\dfrac{3x-15}{2\left(x+1\right)}\)