giải phương trình :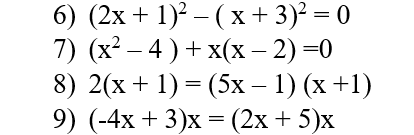
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 4:
\(a)x-7< 2-x\\ \Leftrightarrow x+x< 2+7\\ \Leftrightarrow2x< 9\\ \Leftrightarrow x< \dfrac{9}{2}\\ b)x+2\le2+3x\\ \Leftrightarrow3x-x\ge2-2=0\\ \Leftrightarrow2x\ge0\\ \Leftrightarrow x\ge0\\ c)4+x>5-3x\\ \Leftrightarrow x+3x>5-4\\ \Leftrightarrow4x>1\\ \Leftrightarrow x>\dfrac{1}{4}\\ d)-x+7\ge x-3\\ \Leftrightarrow x+x\le7+3\\ \Leftrightarrow2x\le10\\ \Leftrightarrow x\le\dfrac{10}{2}=5\)

\(\dfrac{3}{x}+\dfrac{4}{x-1}=\dfrac{5x-2}{x^2-x}\left(x\notin\left\{0;1\right\}\right)\\ \Leftrightarrow\dfrac{3\left(x-1\right)}{x\left(x-1\right)}+\dfrac{4x}{x\left(x-1\right)}=\dfrac{5x-1}{x\left(x-1\right)}\\ \Leftrightarrow3\left(x-1\right)+4x=5x-1\\ \Leftrightarrow3x-3+4x=5x-1\\ \Leftrightarrow7x-3=5x+1\\ \Leftrightarrow7x-5x=1+3\\ \Leftrightarrow2x=4\\ \Leftrightarrow x=\dfrac{4}{2}\\ \Leftrightarrow x=2\left(tm\right)\)

a: Ta có: ΔOCK vuông tại C
=>\(CK^2+CO^2=OK^2\)
=>\(CK=\sqrt{10^2-8^2}=6\left(cm\right)\)
Xét ΔOCK vuông tại C có CA là đường cao
nên \(OA\cdot OK=OC^2;CA\cdot OK=CO\cdot CK\)
=>\(OA=\dfrac{OC^2}{OK}=\dfrac{8^2}{10}=6,4\left(cm\right);CA=\dfrac{6\cdot8}{10}=4,8\left(cm\right)\)
Xét ΔCOK vuông tại C có \(sinCOK=\dfrac{CK}{OK}=\dfrac{6}{10}=\dfrac{3}{5}\)
nên \(\widehat{COK}=\widehat{xOy}\simeq36^052'\)
b: Xét ΔCAO vuông tại A có AH là đường cao
nên \(CH\cdot CO=CA^2\left(1\right)\)
Xét ΔCOK vuông tại O có CA là đường cao
nên \(AO\cdot AK=AC^2\left(2\right)\)
Từ (1),(2) suy ra \(CH\cdot CO=AO\cdot AK\)

Xét đường tròn (O) có tiếp tuyến MB tại B nên
\(\widehat{MBI}=\dfrac{1}{2}sđ\stackrel\frown{IB}\)
Lại có \(\widehat{IBH}=90^o-\widehat{BIH}\)
\(=90^o-\widehat{OIB}\)
\(=90^o-\dfrac{180^o-\widehat{IOB}}{2}\)
\(=\dfrac{180^o-180^o+sđ\stackrel\frown{IB}}{2}\)
\(=\dfrac{1}{2}sđ\stackrel\frown{IB}\)
Do đó \(\widehat{MBI}=\widehat{IBH}\) hay BI là tia phân giác của \(\widehat{MBH}\)
\(\Rightarrow d\left(I,MB\right)=d\left(I,BH\right)=IH=R_I\)
Suy ra MB là tiếp tuyến của (I)

\(\left\{{}\begin{matrix}x-ay=a\\ax+y=1\end{matrix}\right.\)
Để hpt có nghiệm thì: \(\dfrac{1}{a}\ne\dfrac{-a}{1}\Leftrightarrow a^2\ne-1\) (luôn đúng)
\(\Leftrightarrow\left\{{}\begin{matrix}x-ay=a\\a^2x+ay=a\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(a^2+1\right)x=2a\\ax+y=1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{2a}{a^2+1}\\\dfrac{2a^2}{a^2+1}+y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{2a}{a^2+1}\\y=1-\dfrac{2a^2}{a^2+1}=\dfrac{1-a^2}{a^2+1}\end{matrix}\right.\)
Ta có: \(\left\{{}\begin{matrix}\text{x}>0\\y>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2a}{a^2+1}>0\\\dfrac{1-a^2}{a^2+1}>0\end{matrix}\right.\)
Mà: \(a^2+1>0\forall a=>\left\{{}\begin{matrix}2a>0\\1-a^2>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a>0\\-1< a< 1\end{matrix}\right.\Leftrightarrow0< a< 1\)

\(\dfrac{3}{4}x-6< =0\)
=>\(\dfrac{3}{4}x< =6\)
=>\(x< =6:\dfrac{3}{4}=6\cdot\dfrac{4}{3}=8\)

không hiểu chỗ nào cứ hỏi nha
a: \(\left\{{}\begin{matrix}4x+3y=6\\5x-y=11\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4x+3y=6\\15x-3y=33\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4x+3y+15x-3y=6+33\\5x-y=11\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}19x=39\\y=5x-11\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{39}{19}\\y=5\cdot\dfrac{39}{19}-11=-\dfrac{14}{19}\end{matrix}\right.\)
b: \(\left\{{}\begin{matrix}\dfrac{1}{5}x-\dfrac{1}{6}y=0\\5x-4y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{x}{5}=\dfrac{y}{6}\\5x-4y=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{5}{6}y\\5\cdot\dfrac{5}{6}y-4y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{5}{6}y\\\dfrac{25}{6}y-4y=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{5}{6}y\\\dfrac{1}{6}y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=12\\x=\dfrac{5}{6}\cdot12=10\end{matrix}\right.\)
c: \(\left\{{}\begin{matrix}\dfrac{1}{3}x-\dfrac{1}{8}y=3\\7x+9y=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{x}{3}-\dfrac{y}{8}=3\\7x+9y=-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{8x-3y}{24}=3\\7x+9y=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}8x-3y=72\\7x+9y=-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}24x-9y=216\\7x+9y=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}24x-9y+7x+9y=216-2\\8x-3y=72\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}31x=214\\3y=8x-72\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{214}{31}\\y=\dfrac{8x-72}{3}=\dfrac{-520}{93}\end{matrix}\right.\)

a: \(\left\{{}\begin{matrix}4x+3y=6\\5x-y=11\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4x+3y=6\\15x-3y=33\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4x+3y+15x-3y=6+33\\5x-y=11\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}19x=39\\y=5x-11\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{39}{19}\\y=5\cdot\dfrac{39}{19}-11=-\dfrac{14}{19}\end{matrix}\right.\)
b: \(\left\{{}\begin{matrix}\dfrac{1}{5}x-\dfrac{1}{6}y=0\\5x-4y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{x}{5}=\dfrac{y}{6}\\5x-4y=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{5}{6}y\\5\cdot\dfrac{5}{6}y-4y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{5}{6}y\\\dfrac{25}{6}y-4y=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{5}{6}y\\\dfrac{1}{6}y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=12\\x=\dfrac{5}{6}\cdot12=10\end{matrix}\right.\)
c: \(\left\{{}\begin{matrix}\dfrac{1}{3}x-\dfrac{1}{8}y=3\\7x+9y=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{x}{3}-\dfrac{y}{8}=3\\7x+9y=-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{8x-3y}{24}=3\\7x+9y=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}8x-3y=72\\7x+9y=-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}24x-9y=216\\7x+9y=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}24x-9y+7x+9y=216-2\\8x-3y=72\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}31x=214\\3y=8x-72\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{214}{31}\\y=\dfrac{8x-72}{3}=\dfrac{-520}{93}\end{matrix}\right.\)

a: \(\left\{{}\begin{matrix}4x+3y=6\\5x-y=11\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4x+3y=6\\15x-3y=33\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4x+3y+15x-3y=6+33\\5x-y=11\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}19x=39\\y=5x-11\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{39}{19}\\y=5\cdot\dfrac{39}{19}-11=-\dfrac{14}{19}\end{matrix}\right.\)
b: \(\left\{{}\begin{matrix}\dfrac{1}{5}x-\dfrac{1}{6}y=0\\5x-4y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{x}{5}=\dfrac{y}{6}\\5x-4y=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{5}{6}y\\5\cdot\dfrac{5}{6}y-4y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{5}{6}y\\\dfrac{25}{6}y-4y=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{5}{6}y\\\dfrac{1}{6}y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=12\\x=\dfrac{5}{6}\cdot12=10\end{matrix}\right.\)
c: \(\left\{{}\begin{matrix}\dfrac{1}{3}x-\dfrac{1}{8}y=3\\7x+9y=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{x}{3}-\dfrac{y}{8}=3\\7x+9y=-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{8x-3y}{24}=3\\7x+9y=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}8x-3y=72\\7x+9y=-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}24x-9y=216\\7x+9y=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}24x-9y+7x+9y=216-2\\8x-3y=72\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}31x=214\\3y=8x-72\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{214}{31}\\y=\dfrac{8x-72}{3}=\dfrac{-520}{93}\end{matrix}\right.\)





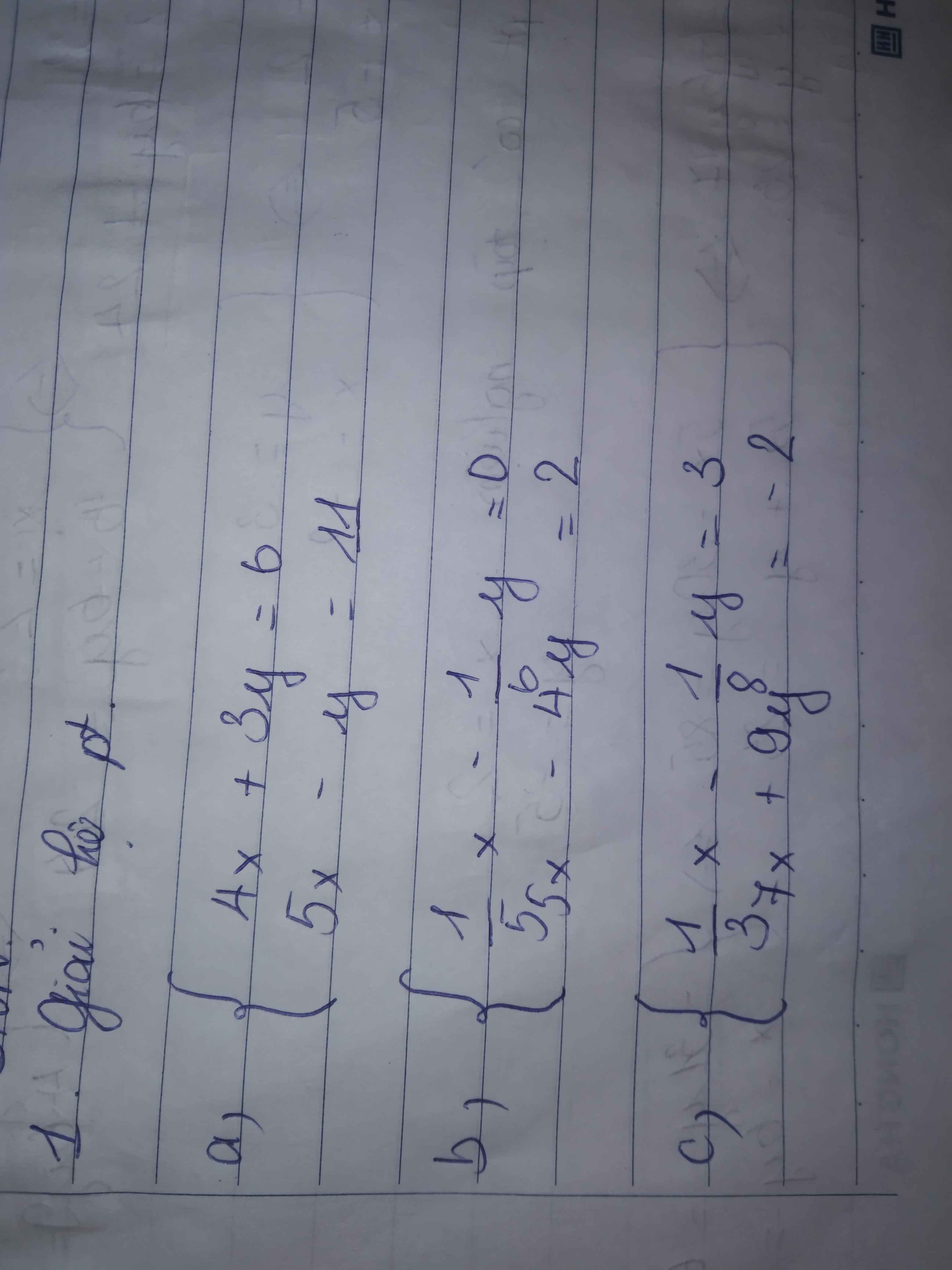
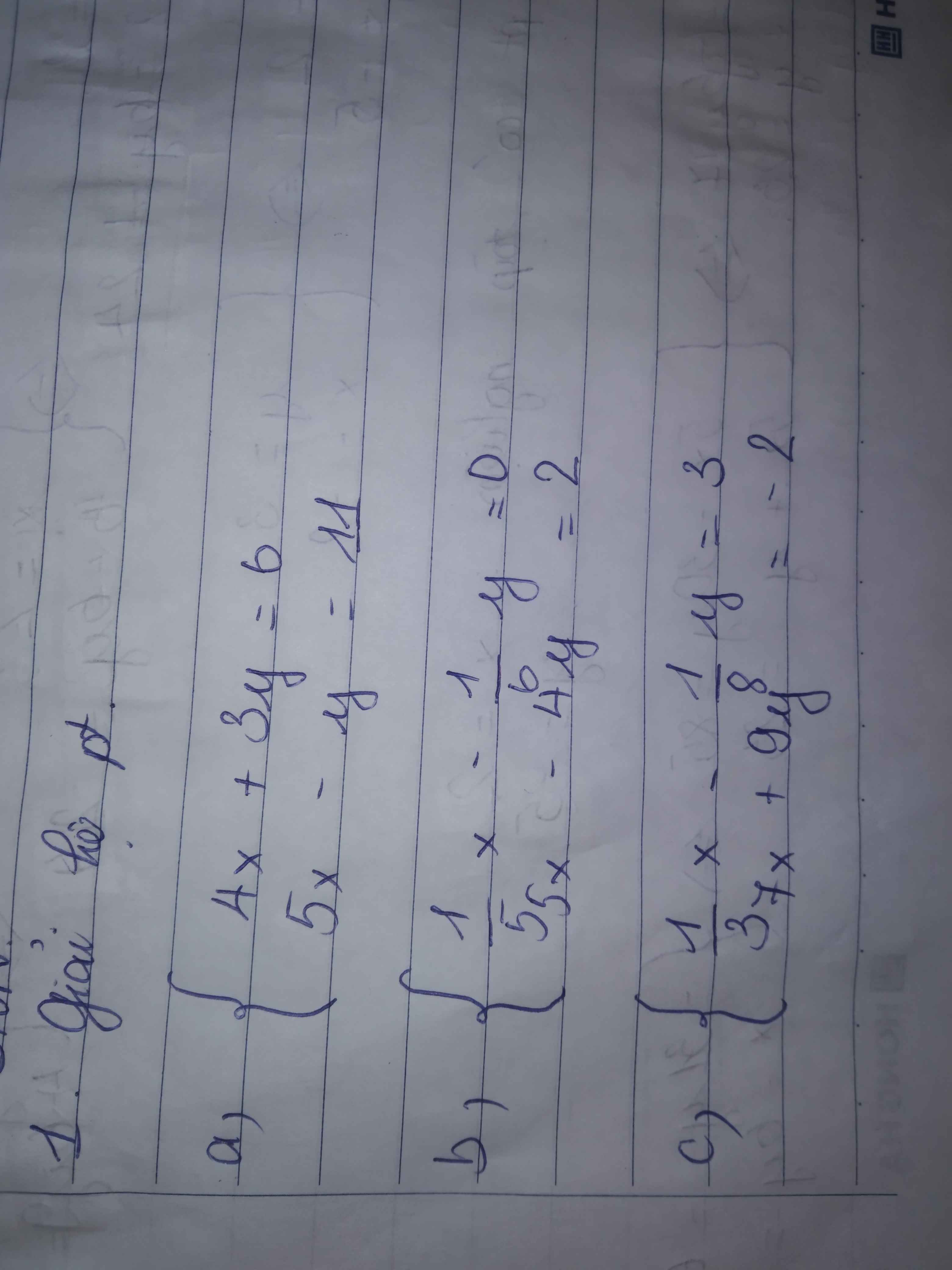
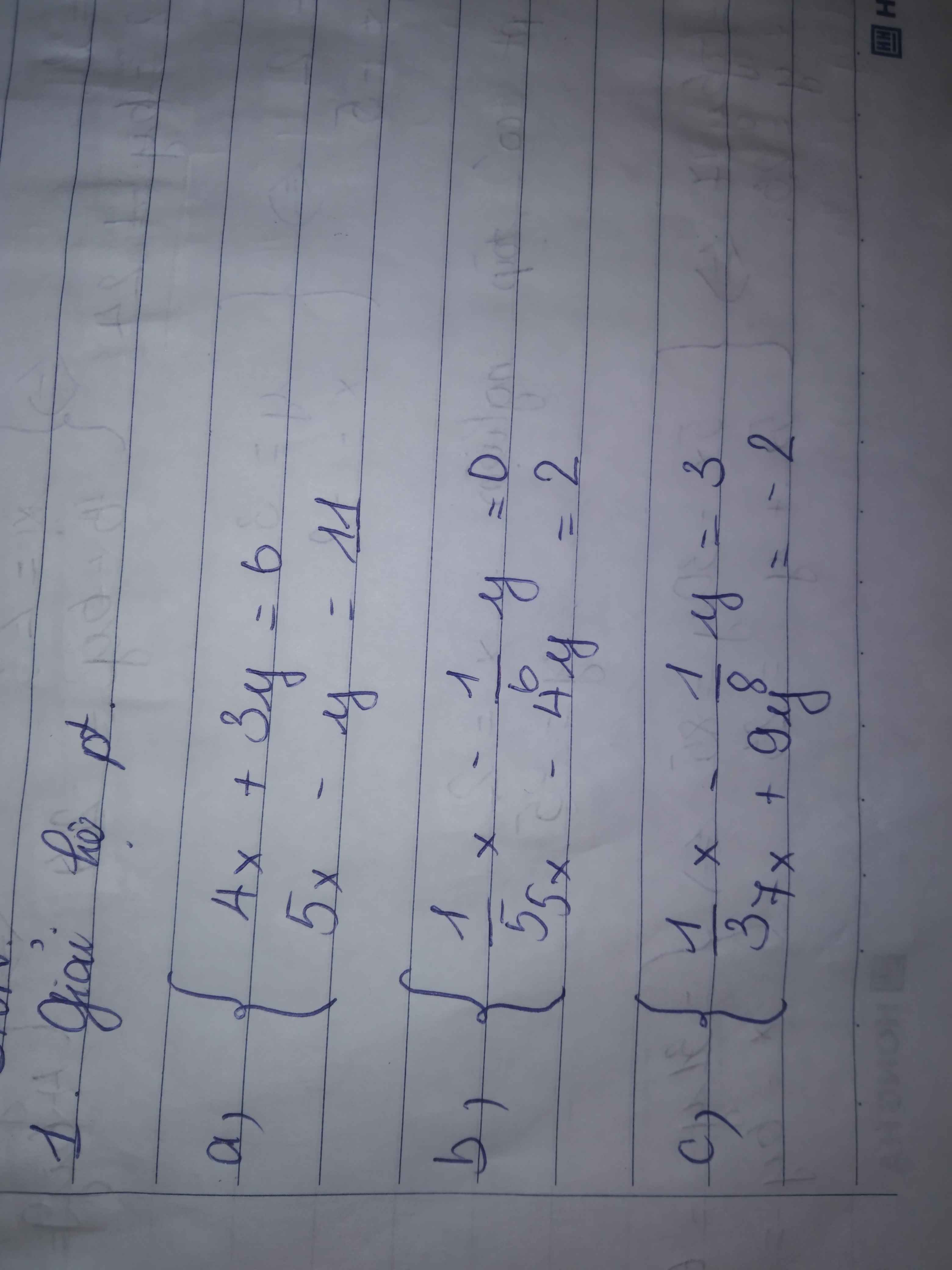
\(6)\left(2x+1\right)^2-\left(x+3\right)^2=0\\ \Leftrightarrow\left(2x+1-x-3\right)\left(2x+1+x+3\right)=0\\ \Leftrightarrow\left(x-2\right)\left(3x+4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x-2=0\\3x+4=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=2\\x=-\dfrac{4}{3}\end{matrix}\right.\\ 7)\left(x^2-4\right)+x\left(x-2\right)=0\\ \Leftrightarrow\left(x-2\right)\left(x+2\right)+x\left(x-2\right)=0\\ \Leftrightarrow\left(x-2\right)\left(x+2+x\right)=0\\ \Leftrightarrow\left(x-2\right)\left(2x+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x-2=0\\2x+2=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\\ 8)2\left(x+1\right)=\left(5x-1\right)\left(x+1\right)\\ \Leftrightarrow2\left(x+1\right)-\left(5x-1\right)\left(x+1\right)=0\\ \Leftrightarrow\left(x+1\right)\left(2-5x+1\right)=0\\ \Leftrightarrow\left(x+1\right)\left(3-5x\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=-1\\x=\dfrac{3}{5}\end{matrix}\right.\\ 9)\left(-4x+3\right)x=\left(2x+5\right)x\\ \Leftrightarrow\left(-4x+3\right)x-\left(2x+5\right)x=0\\ \Leftrightarrow x\left(-4x+3-2x-5\right)=0\\ \Leftrightarrow x\left(-6x-2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=-\dfrac{1}{3}\end{matrix}\right.\)