Xét A=(5/4x23)+(3/4.31)+(4/5x31)+(6/5x41) và B=(1/6x23)+(5/6x29)+(3/6x29)+(9/8x41) tính hiệu A-B . nhanh gúp mình ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


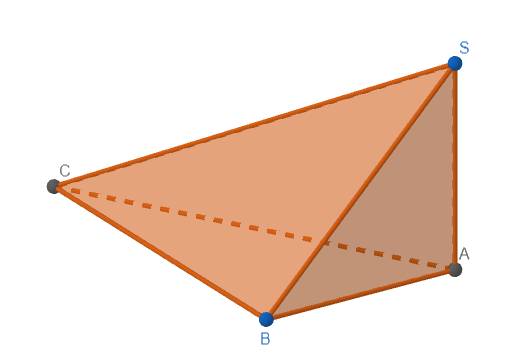
Ta có \(SA\perp\left(ABC\right)\) nên \(SA\perp BC\)
Lại có \(BC\perp AB\) nên \(CB\perp\left(SAB\right)\)
Do đó \(\widehat{SC,\left(SAB\right)}=\widehat{CSB}\)
Mặt khác, \(CB\perp\left(SAB\right)\Rightarrow CB\perp SB\) \(\Rightarrow\Delta SBC\) vuông tại B
Có \(SC=\sqrt{SA^2+AC^2}=\sqrt{a^2+\left(2a\right)^2}=a\sqrt{5}\)
\(CB=AC.\cos30^o=2a.\dfrac{\sqrt{3}}{2}=a\sqrt{3}\)
\(\Rightarrow\sin\widehat{CSB}=\dfrac{CB}{CS}=\dfrac{a\sqrt{3}}{a\sqrt{5}}=\sqrt{\dfrac{3}{5}}\)
\(\Rightarrow\widehat{CSB}=arc\sin\left(\sqrt{\dfrac{3}{5}}\right)\approx50,768^o\)
Vậy \(\widehat{SC,\left(SAB\right)}\approx50,768^o\)
Mình gửi đáp án rồi đó nhưng vì có hình nên nó chưa duyệt lên được. Bạn vào trang cá nhân của mình xem nhé.

Lời giải:
Vì $y^2\geq 0$ với mọi $y$ nên $14(x-2023)^2=26-3y^2\leq 26$
$\Rightarrow (x-2023)^2\leq \frac{26}{14}< 2$
Mà $(x-2023)^2$ là scp nên $(x-2023)^2=0$ hoặc $(x-2023)^2=1$
Nếu $(x-2023)^2=0$ thì: $26-3y^2=0\Rightarrow y^2=\frac{26}{3}$ (vô lý - loại)
Nếu $(x-2023)^2=1$ thì:
$x-2023=\pm 1\Rightarrow x=2022$ hoặc $x=2024$
$26-3y^2=14\Rightarrow 3y^2=12\Rightarrow y^2=4\Rightarrow y=\pm 2$
Vậy $(x,y)=(2022, 2), (2022, -2), (2024,2), (2024,-2)$
