thu gọn biểu thức C D biết: C=5^3 +5^5+ ... +5^101 và D=1+ 3^2+ 3^4+ 3^6+ ... +3^100
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


C = 53 + 55 + ... + 5101
52.C = 55 + 57 + ... + 5103
25.C - C = (55 + 57 + ... + 5103) - (53 + 55 + ... + 5101)
24C = 55 + 57 + ... + 5103 - 53 - 55 - ... - 5101
24C = (55 - 55) + (57 - 57) +...+ (5101 - 5101) + 5103 - 53
24C = 5103 - 53
C = \(\dfrac{5^{103}-5^3}{24}\)

Lời giải:
Đặt $\frac{a}{b}=\frac{c}{d}=k\Rightarrow a=bk, c=dk$. Khi đó:
$\frac{a}{b}=\frac{bk}{b}=k(1)$
$\frac{a^2+c^2}{b^2+c^2}=\frac{(bk)^2+(dk)^2}{b^2+(dk)^2}=\frac{k^2(b^2+d^2)}{b^2+d^2k^2}(2)$
Từ $(1); (2)$ suy ra đề sai.

Đặt: \(\dfrac{x}{4}=\dfrac{y}{7}=k\)
\(\Rightarrow\left\{{}\begin{matrix}x=4k\\y=7k\end{matrix}\right.\)
Ta có: \(xy=112\Rightarrow4k\cdot7k=112\)
\(\Rightarrow28k^2=112\)
\(\Rightarrow k^2=4\)
\(\Rightarrow\left[{}\begin{matrix}k=-2\\k=2\end{matrix}\right.\)
Với k = -2
\(\Rightarrow\left\{{}\begin{matrix}x=4\cdot-2=-8\\y=7\cdot-2=-14\end{matrix}\right.\)
Với k = 2
\(\Rightarrow\left\{{}\begin{matrix}x=4\cdot2=8\\y=7\cdot2=14\end{matrix}\right.\)

a, △ABC = △NMP
b, em xem lại em ghi đúng đề chưa
c, △ABC = △PNM
d, △ABC = △PMN
e, △ABC = △NPM

A B C K x y
Xét tg ABC có
\(\widehat{B}+\widehat{C}=180^o-\widehat{A}=180^o-68^o=112^o\)
\(\widehat{KBC}=\dfrac{\widehat{ABx}-\widehat{B}}{2}=\dfrac{180^o-\widehat{B}}{2}=90^o-\dfrac{\widehat{B}}{2}\)
\(\widehat{KCB}=\dfrac{\widehat{ACy}-\widehat{C}}{2}=\dfrac{180^o-\widehat{C}}{2}=90^o-\dfrac{\widehat{C}}{2}\)
Xét tg KBC có
\(\widehat{BKC}=180^o-\left(\widehat{KBC}+\widehat{KCB}\right)=\)
\(=180^o-\left(90^o-\dfrac{\widehat{B}}{2}+90^o-\dfrac{\widehat{C}}{2}\right)=\dfrac{\widehat{B}+\widehat{C}}{2}=\dfrac{112^o}{2}=56^o\)

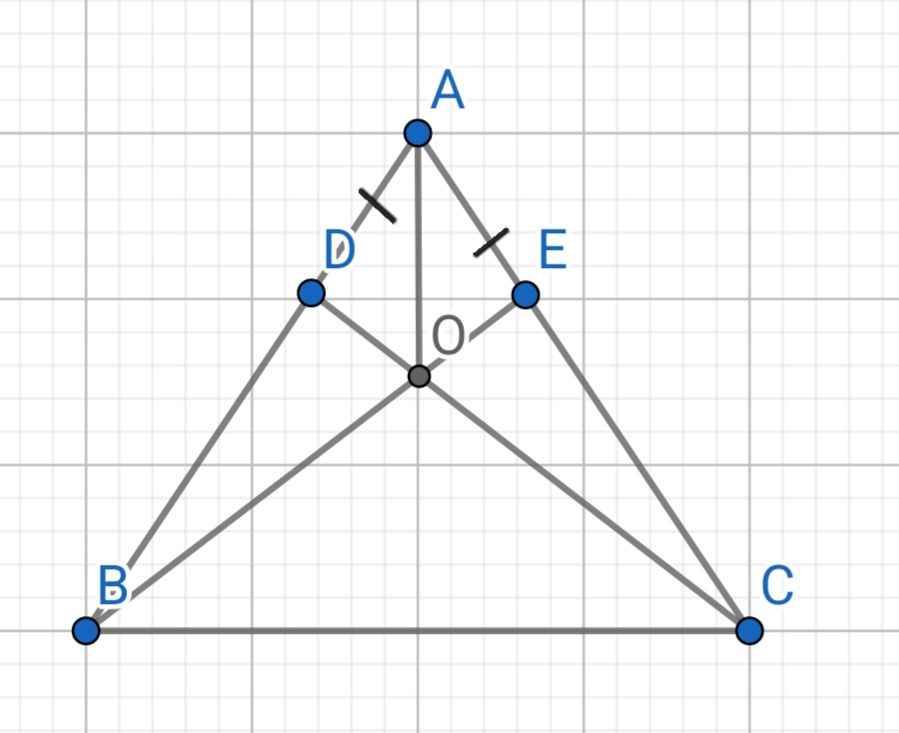 ∆ABC có:
∆ABC có:
AB = AC (gt)
⇒ ∆ABC cân tại A
⇒ ∠ABC = ∠ACB
⇒ ∠DBC = ∠ECB
Do AB = AC (gt)
AD = AE (gt)
⇒ BD = AB - AD = AC - AE = CE
Xét ∆DBC và ∆ECB có:
DB = EC (cmt)
∠DBC = ∠ECB (cmt)
BC là cạnh chung
⇒ ∆DBC = ∆ECB (c-g-c)
⇒ ∠BDC = ∠CEB (hai góc tương ứng)
⇒ ∠BDO = ∠CEO
Do ∆DBC = ∆ECB (cmt)
⇒ ∠BCD = ∠CBE (hai góc tương ứng)
Mà ∠ACB = ∠ABC (cmt)
⇒ ∠ECO = ∠ACB - ∠BCD
= ∠ABC - ∠CBE
= ∠DBO
Xét ∆BOD và ∆COE có:
∠DBO = ∠ECO (cmt)
BD = CE (cmt)
∠BDO = ∠CEO (cmt)
⇒ ∆BOD = ∆COE (g-c-g)
⇒ OD = OE (hai cạnh tương ứng)
Xét ∆ADO và ∆AEO có:
AD = AE (gt)
AO là cạnh chung
OD = OE (cmt)
∆ADO = ∆AEO (c-c-c)
⇒ ∠DAO = ∠EAO (hai góc tương ứng)
⇒ AO là tia phân giác của ∠DAE
Hay AO là tia phân giác của ∠BAC

Ta có: Vì B=20o, C = 40o nên A bằng 120o
=>ABC là tam giác tù
Vì AD phân giác CAB nên CAD=60o
=>CDA=180-40-60=80o
Vậy CDA=60o


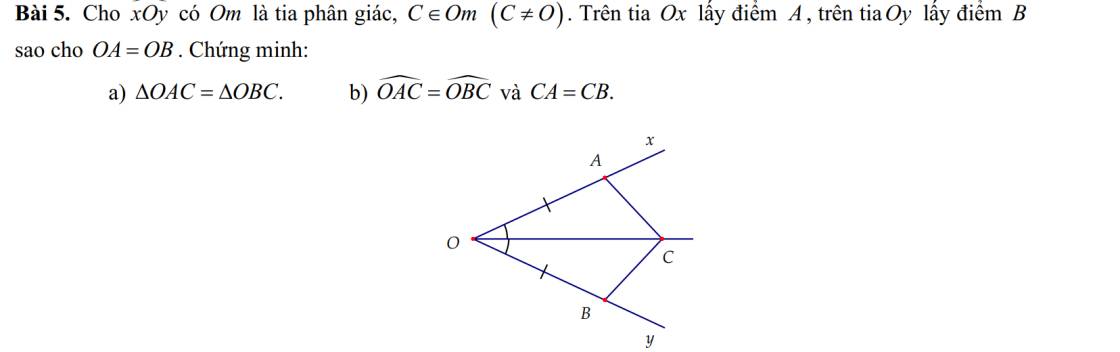
Do Om là tia phân giác của xOy (gt)
⇒ ∠xOm = ∠yOm
⇒ ∠AOC = ∠BOC
Xét ∆OAC và ∆OBC có:
OA = OB (gt)
∠AOC = ∠BOC (cmt)
OC là cạnh chung
⇒ ∆OAC = ∆OBC (c-g-c)
b) Do ∆OAC = ∆OBC (cmt)
⇒ ∠OAC = ∠OBC (hai góc tương ứng)
Do ∆OAC = ∆OBC (cmt)
⇒ CA = CB (hai cạnh tương ứng)
C= 53+55+... +5101
⇔25C= 55+ 57+...+5103
⇔25C-C=(55+57+...+5103) - ( 53+55+...+5101)
⇔24C=5103 - 53
⇔C=(5103 - 53 ) / 24
CMTT : D=1 + 32+34+36+ ... + 3100
⇔9D= 32+34+36+38+...+ 3102
⇔9D-D=(32+34+36+38+...+ 3102) - (1 + 32+34+36+ ... + 3100)
⇔8D=3102-1
⇔D=(3102-1)/8
Để thu gọn biểu thức \( C D \), chúng ta cần tính giá trị của \( C \) và \( D \) trước.
Đầu tiên, ta tính giá trị của \( C \):
\[ C = 5^{3} + 5^{5} + \ldots + 5^{101} \]
Đây là một dãy số hình học với công bội là 5. Ta có thể sử dụng công thức tổng của dãy số hình học để tính tổng này. Công thức tổng của dãy số hình học là:
\[ S = \frac{a(1 - r^n)}{1 - r} \]
Trong đó:
- \( S \) là tổng của dãy số hình học
- \( a \) là số hạng đầu tiên của dãy
- \( r \) là công bội của dãy
- \( n \) là số lượng số hạng trong dãy
Áp dụng công thức này vào biểu thức \( C \), ta có:
\[ C = \frac{5^3(1 - 5^{99})}{1 - 5} \]
Tiếp theo, ta tính giá trị của \( D \):
\[ D = 1 + 3^2 + 3^4 + \ldots + 3^{100} \]
Đây là một dãy số hình học với công bội là 9. Ta cũng có thể sử dụng công thức tổng của dãy số hình học để tính tổng này. Áp dụng công thức này vào biểu thức \( D \), ta có:
\[ D = \frac{1(1 - 3^{100})}{1 - 3^2} \]
Cuối cùng, để thu gọn biểu thức \( C D \), ta tính giá trị của \( C D \) bằng cách nhân giá trị của \( C \) và \( D \):
\[ C D = \frac{5^3(1 - 5^{99})}{1 - 5} \times \frac{1(1 - 3^{100})}{1 - 3^2} \]
Bạn có thể tính giá trị cuối cùng của biểu thức \( C D \) bằng cách thực hiện các phép tính trên.