Lời giải:

a. Tổng độ dài hai đáy:
$48\times 2:6=16$ (cm) 

Độ dài đáy nhỏ: $(16-4):2=6$ (cm) 

Độ dài đáy lớn: $6+4=10$ (cm) 

b. 

$S_{ABD}=AB\times h:2=6\times 6:2=18$ (cm²)

$S_{ABC}=AB\times h:2 = 6\times 6:2=18$ (cm²)

$\Rightarrow S_{ABD}=S_{ABC}$

$\Rightarrow S_{ABD}-S_{AOB}=S_{ABC}-S_{AOB}$

$\Rightarrow S_{AOD}=S_{BOC}$

d.

$\frac{S_{AOB}}{S_{AOD}}=\frac{OB}{OD}$

$\Rightarrow S_{AOB}=\frac{OB}{OD}\times S_{AOD}$
$\frac{S_{BOC}}{S_{DOC}}=\frac{OB}{OD}$

$\Rightarrow S_{BOC}=\frac{OB}{OD}\times S_{DOC}$

Suy ra:

$S_{AOB}+S_{BOC}=\frac{OB}{OD}\times (S_{AOD}+S_{DOC})$

$S_{ABC}=\frac{OB}{OD}\times S_{ADC}$

$6\times 6:2=\frac{OB}{OD}\times 10\times 6:2$

$18=\frac{OB}{OD}\times 30$

$\frac{OB}{OD}=\frac{18}{30}=\frac{3}{5}$

$\Rightarrow \frac{OB}{BD}=\frac{3}{8}$
$\frac{S_{AOB}}{S_{ABD}}=\frac{OB}{BD}=\frac{3}{8}$

$\Rightarrow S_{AOB}=\frac{3}{8}\times S_{ABD}=\frac{3}{8}\times 18=6,75$ (cm²)

Hình vẽ:

12. D

13. D

14. A

15. B

16. C

17. A

18. A

19. A

12. D

13.D

14.A

15.B

16.C

17.A (Mình không chắc lắm )

18.A

19.A

Xin các bạn giúp ạ!

giải rồi mà

A. Me

A

\(3-\left(\dfrac{1}{6}+x\right)\cdot\dfrac{2}{3}=\dfrac{2}{3}\\ \left(\dfrac{1}{6}+x\right)\cdot\dfrac{2}{3}=\dfrac{7}{3}\\ \dfrac{1}{6}+x=\dfrac{7}{2}\\ x=\dfrac{7}{2}-\dfrac{1}{6}=\dfrac{10}{3}\)

HD:

\(\dfrac{2}{3}\) x\(\left(\dfrac{1}{6}+x\right)=3-\dfrac{2}{3}\)

\(\left(\dfrac{1}{6}+x\right)=\dfrac{7}{3}:\dfrac{2}{3}\)

\(x=\dfrac{7}{2}-\dfrac{1}{6}\)

\(x=\dfrac{10}{3}\)

\(\dfrac{6}{5}+\left[\dfrac{1}{12}\cdot\left(x-2\right)\right]:\dfrac{1}{18}=\dfrac{21}{10}\\ \left[\dfrac{1}{12}\cdot\left(x-2\right)\right]:\dfrac{1}{18}=\dfrac{9}{10}\\ \dfrac{1}{12}\cdot\left(x-2\right)=\dfrac{1}{20}\\ x-2=\dfrac{3}{5}\\ x=\dfrac{13}{5}\)

Theo bài ra, ta có sơ đồ:Tổng số phần bằng nhau :

3 + 1 + 3 = 7 (phần)

Giá trị 7 phần:

420 - 14 = 406

Số thứ hai là:

  406 : 7 = 58

Số thứ nhất là:

  58 x 3 = 174

Số thứ ba là:

  174 + 14 = 188

a. ( 24 x 3 + 56 x 2 ) : ( 96 : 24 )

= ( 72 + 56 x 2 ) : ( 96 : 24 )

= ( 72 + 112 ) : ( 96 : 24 )

= ( 72 + 112 ) : 4

= 184 : 4

= 46

b. 481 : ( 21 + 16 ) x 21

= 481 : 37 x 21

= 13 x 21

= 273

giup tui voi troiiiii oiii

Lời giải:

Gọi số thứ ba là $x$. 

Theo bài ra thì:

Số thứ hai là: $2\times x+1$

Số thứ nhất là: $2\times (2\times x+1)+1=4\times x+3$

Tổng ba số: $4\times x+3+2\times x+1+x=123$

$7\times x+4=123$

$7\times x=119$

$x=119:7=17$

Vậy số thứ ba là 17. Số thứ hai là $17\times 2+1=35$. Số thứ nhất là $35\times 2+1=71$

Tổng 3 số là:

  75 x 3 = 225

Nếu thêm chữ số 0 vào bên phải số thứ hai thì được số thứ nhất

Do đó nên số thứ nhất gấp 10 lần số thứ hai

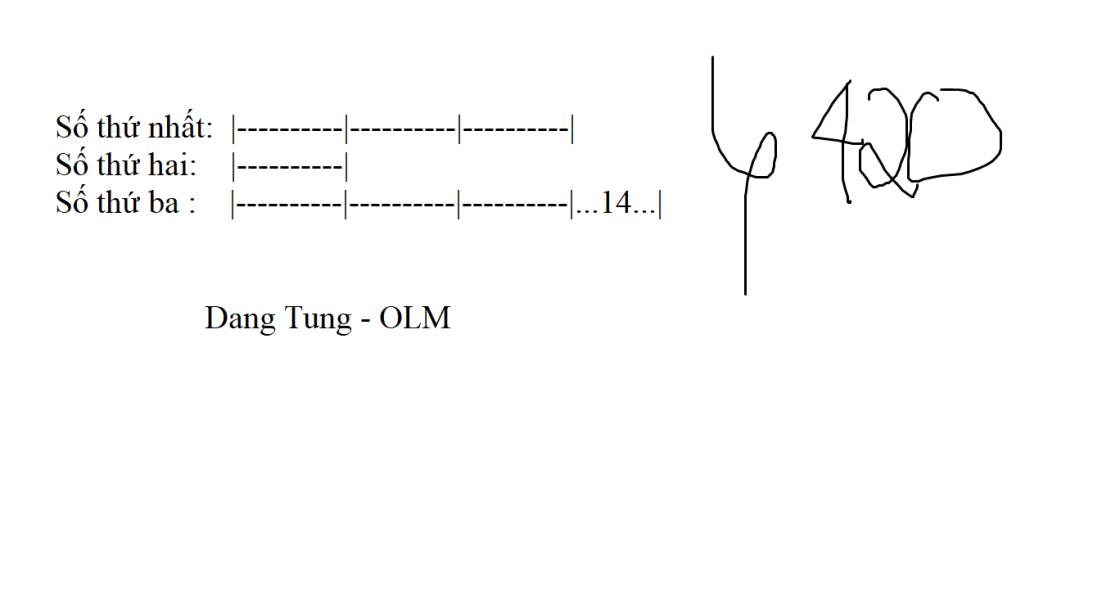
Ta có sơ đồ:

Số thứ nhất: |--|--|--|--|--|--|--|--|--|--|

Số thứ hai:   |--|

Số thứ ba:    |--|--|--|--|

Tổng số phần bằng nhau là:

  10 + 1 + 4 = 15 (phần)

Số thứ hai là:

  225 : 15 = 15

Số thứ ba là:

  15 x 4 = 60

Số thứ nhất là :

  15 x 10 = 150