Bác dũng cần di chuyển một đoạn đường dài 6km nên đã đi tắc xi, đến nơi tài xế nói rằng: với 2km đầu tiên giá cước là 29 000 đồng và 4km tiếp theo giá cước là 10 000 đồng cho mỗi một km. Hỏi bác Dũng cần trả cho tài xế bao nhiêu tiền?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1000 - 94 - 81 - 50 - 10
= (1000 - 50 - 10) - 94 - 81
= (950 - 10) - 94 - 81
= 940 - 94 - 81
= 846 - 81
= 765

Olm chào em, cảm ơn đánh giá của em về chất lượng bài giảng của Olm, cảm ơn em đã đồng hành cùng Olm trên hành trình tri thức. Chúc em học tập hiệu quả và vui vẻ cùng Olm em nhé!

\(\dfrac{1}{4}+\dfrac{1}{9}=\dfrac{9}{36}+\dfrac{4}{36}=\dfrac{9+4}{36}=\dfrac{13}{36}\)

Giải:
Thời gian Mai đi đến trường là:
7 giờ 10 phút - 6 giờ 45 phút = 25 phút
Đáp số: 25 phút
đổi/7giờ10 phút =6giờ70phút
thời gian mai đi từ nhà đến trường là
6giờ70phút trừ 6giờ 45phút=25phút
đáp số 25phút

a: Sửa đề: \(S=\dfrac{1}{\sqrt{1}+\sqrt{5}}+\dfrac{1}{\sqrt{5}+\sqrt{9}}+...+\dfrac{1}{\sqrt{4n-3}+\sqrt{4n+1}}\)
\(=\dfrac{-\sqrt{1}+\sqrt{5}}{4}+\dfrac{-\sqrt{5}+\sqrt{9}}{4}+...+\dfrac{-\sqrt[]{4n-3}+\sqrt{4n+1}}{4}\)
\(=\dfrac{-\sqrt{1}+\sqrt{5}-\sqrt{5}+\sqrt{9}-...-\sqrt{4n-3}+\sqrt{4n+1}}{4}=\dfrac{\sqrt{4n+1}-1}{4}\)
b: \(T=\dfrac{\sqrt{2-\sqrt{3}}}{1-\sqrt{3}}-\dfrac{\sqrt{5-\sqrt{21}}}{\sqrt{3}-\sqrt{7}}\)
\(=\dfrac{1}{\sqrt{2}}\left(\dfrac{\sqrt{4-2\sqrt{3}}}{1-\sqrt{3}}-\dfrac{\sqrt{10-2\sqrt{21}}}{\sqrt{3}-\sqrt{7}}\right)\)
\(=\dfrac{1}{\sqrt{2}}\cdot\left(\dfrac{\sqrt{\left(\sqrt{3}-1\right)^2}}{1-\sqrt{3}}-\dfrac{\sqrt{\left(\sqrt{7}-\sqrt{3}\right)^2}}{\sqrt{3}-\sqrt{7}}\right)\)
\(=\dfrac{1}{\sqrt{2}}\cdot\left(\dfrac{\sqrt{3}-1}{1-\sqrt[]{3}}-\dfrac{\sqrt{7}-\sqrt{3}}{\sqrt{3}-\sqrt{7}}\right)\)
\(=\dfrac{1}{\sqrt{2}}\left(-1+\dfrac{\sqrt{7}-\sqrt{3}}{\sqrt{7}-\sqrt{3}}\right)=0\)

Ta có: \(\dfrac{x-1}{3}=\dfrac{x-2}{2}\)
=>3(x-2)=2(x-1)
=>3x-6=2x-2
=>3x-2x=-2+6
=>x=4


Olm chào em, cảm ơn đánh giá của em về chất lượng bài giảng của Olm, cảm ơn em đã đồng hành cùng Olm trên hành trình tri thức. Chúc em học tập hiệu quả và vui vẻ cùng Olm em nhé!
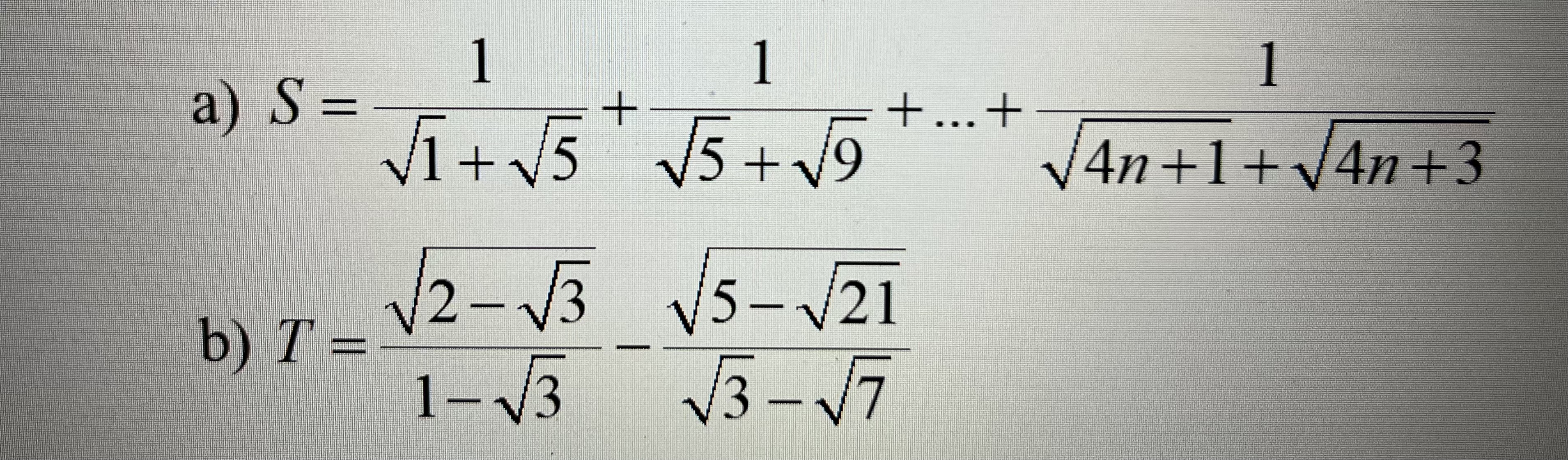
Số tiền phải trả cho 4km tiếp theo là:
10000x4=40000(đồng)
Số tiền bác Dũng cần trả là:
29000+40000=69000(đồng)