Mình có câu đố này:
“Hãy chuẩn bị cho ta 9 cái bánh, nhưng chỉ được đựng vào 4 cái hộp bánh, và mỗi hộp chỉ được đựng đúng 3 cái bánh!”
Ông chủ đang ngơ ngác thì một cậu bé tên Gauss – người sau này trở thành nhà toán học nổi tiếng người Đức – chạy ra giúp ông chủ:
“Xin ngài cứ yên tâm, bánh của ngài sẽ được xếp theo đúng yêu cầu ạ”.
Vậy cậu bé Gauss đã làm cách nào?

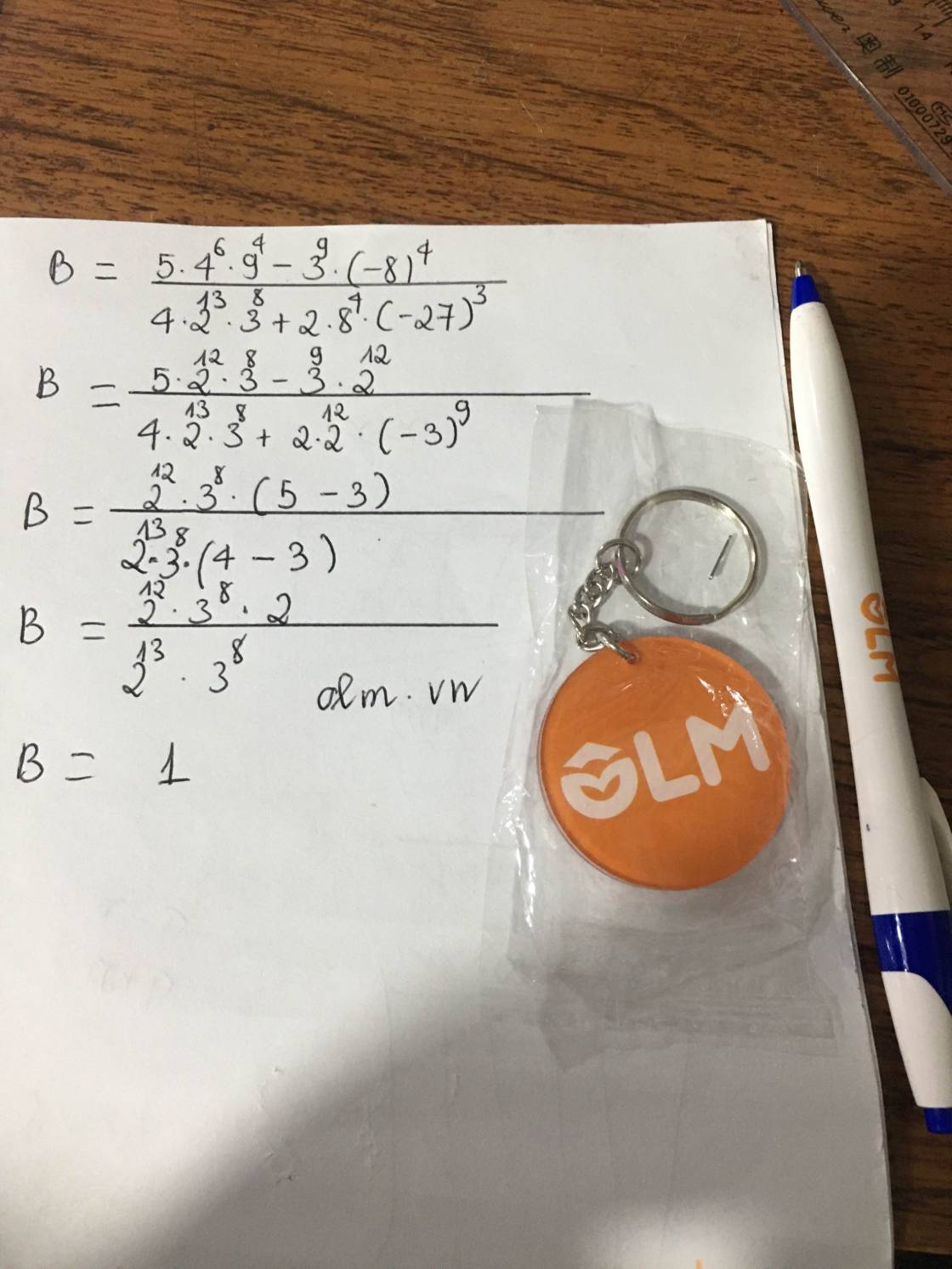
bạn nhận được cái này từ đâu?
Mê tín dị đoan à?
bạn nghĩ tôi tin chắc?