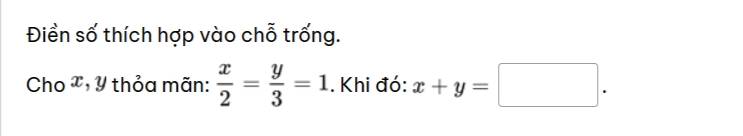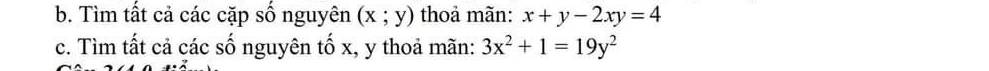Lời giải:

Độ dài đường chéo HCN: $\sqrt{7^2+8^2}=10,6$ (cm)

Đặt \(\widehat{A}=a;\widehat{B}=b;\widehat{C}=c\)

Số đo góc A bằng 6 lần số đo góc B bằng 3 lần số đo góc C

=>a=6b=3c

=>\(\dfrac{a}{6}=\dfrac{6b}{6}=\dfrac{3c}{6}\)

=>\(\dfrac{a}{6}=\dfrac{b}{1}=\dfrac{c}{2}\)

Xét ΔABC có \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)

=>\(a+b+c=180^0\)

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{a}{6}=\dfrac{b}{1}=\dfrac{c}{2}=\dfrac{a+b+c}{6+1+2}=\dfrac{180}{9}=20\)

=>\(a=20\cdot6=120;b=1\cdot20=20;c=2\cdot20=40\)

Vậy: \(\widehat{A}=120^0;\widehat{B}=20^0;\widehat{C}=40^0\)

Lời giải:

Ta có: $\widehat{A}+\widehat{B}+\widehat{C}=180^0$ (tổng 3 góc trong 1 tam giác)

Áp dụng TCDTSBN:

$\widehat{A}=6\widehat{B}=3\widehat{C}=\frac{\widehat{A}}{1}=\frac{\widehat{B}}{\frac{1}{6}}=\frac{\widehat{C}}{\frac{1}{3}}=\frac{\widehat{A}+\widehat{B}+\widehat{C}}{1+\frac{1}{6}+\frac{1}{3}}=\frac{180^0}{\frac{3}{2}}=120^0$

$\Rightarrow \widehat{A}=120^0; \widehat{B}=120^0:6=20^0; \widehat{C}=120^0:3=40^0$

\(\dfrac{x}{2}=\dfrac{y}{3}=1\)

=>\(x=2\cdot1=2;y=3\cdot1=3\)

x+y=2+3=5

Số bánh Khang chia cho Ý là : 20 * 2/5 =8 (cái bánh)

Số bánh còn lại sau khi chia cho Ý là: 20 - 8 = 12 (cái bánh)

Số bánh Khang chia cho Mai  là : 12 * 1/3 = 4 (cái bánh)

Cuối cùng Khang còn lại số bánh là : 12 - 4 = 8 (cái bánh)

Số bánh sau khi chia cho Ý là: 20 * (1-2/5) = 12 cái bánh.

Số bánh sau khi chia cho Mai là: 12 * (1-1/3) = 8 cái bánh

a: Xét ΔAHB và ΔAHC có

AH chung

HB=HC

AB=AC

Do đó: ΔAHB=ΔAHC

=>\(\widehat{BAH}=\widehat{CAH}\)

=>AH là phân giác của góc BAC

b: Ta có: \(\widehat{DHA}=\widehat{HAC}\)(hai góc so le trong, DH//AC)

\(\widehat{DAH}=\widehat{HAC}\)(Cmt)

Do đó: \(\widehat{DHA}=\widehat{DAH}\)

=>ΔDAH cân tại D

c: Xét ΔABC có

H là trung điểm của BC

HD//AC

Do đó:D là trung điểm của AB

Trên tia đối của tia DC lấy K sao cho DK=DC

=>D là trung điểm của CK

Xét ΔDBK và ΔDAC có

DB=DA

\(\widehat{BDK}=\widehat{ADC}\)(hai góc đối đỉnh)

DK=DC

Do đó: ΔDBK=ΔDAC

=>BK=AC

Xét ΔCBK có BK+BC>CK

mà BK=AC và CK=2CD

nên AC+BC>2CD

=>\(CD< \dfrac{AC+BC}{2}\)

CM=1,5MB

=>\(\dfrac{BM}{BC}=\dfrac{2}{5}\)

=>\(S_{AMB}=\dfrac{2}{5}\cdot S_{ABC}=6\left(cm^2\right)\)

BN=1,5AN

=>\(\dfrac{AN}{AB}=\dfrac{2}{5}\)

=>\(S_{ANM}=\dfrac{2}{5}\cdot S_{ABM}=\dfrac{2}{5}\cdot6=2,4\left(cm^2\right)\)

Lời giải:

b.

$x+y-2xy=4$

$\Rightarrow (x-2xy)+y-4=0$

$\Rightarrow x(1-2y)+y-4=0$

$\Rightarrow 2x(1-2y)+2y-8=0$

$\Rightarrow 2x(1-2y)-(1-2y)-7=0$

$\Rightarrow (2x-1)(1-2y)=7$

Do $x,y$ nguyên nên $2x-1,1-2y$ cũng là số nguyên. Mà $(2x-1)(1-2y)=7$ nên xét các TH sau:

TH1: $2x-1=1, 1-2y=7\Rightarrow x=1; y=-3$

TH2: $2x-1=-1, 1-2y=-7\Rightarrow x=0; y=4$

TH3: $2x-1=7, 1-2y=1\Rightarrow x=4; y=0$

TH4: $2x-1=-7, 1-2y=-1\Rightarrow x=-3; y=1$

c.

Nếu $x$ chẵn thì $x=2$. Khi đó: $19y^2=3x^2+1=3.2^2+1=13$ (vô lý) 

Nếu $x$ lẻ thì $19y^2=3x^2+1$ chẵn

$\Rightarrow y$ chẵn

$\Rightarrow y=2$

Khi đó: $3x^2+1=19y^2=19.2^2=76$

$\Rightarrow x^2=25\Rightarrow x=5$ (tm)

Vậy........

  Vận tốc này à bn :)

Gọi vận tốc lúc đầu của người đó là x(km/h)

(Điều kiện: x>0)

Thời gian dự kiến ban đầu là \(\dfrac{90}{x}\left(giờ\right)\)

1h9p=1,15h

Sau 1,15h, người đó đi được 1*x=x(km)

Độ dài quãng đường còn lại là 90-x(km)

Thời gian thực tế đi hết quãng đường là:

\(1,15+\dfrac{90-x}{x+4}\left(giờ\right)\)

Theo đề, ta có: 

\(\dfrac{90}{x}=1,15+\dfrac{90-x}{x+4}\)

=>\(\dfrac{90}{x}-\dfrac{90-x}{x+4}=1,15\)

=>\(\dfrac{90x+360-90x+x^2}{x\left(x+4\right)}=1,15\)

=>\(1,15\left(x^2+4x\right)=x^2+360\)

=>\(1,15x^2+4,6x-x^2-360=0\)

=>\(0,15x^2+4,6x-360=0\)

=>\(\left[{}\begin{matrix}x=36\left(nhận\right)\\x=-\dfrac{200}{3}\left(loại\right)\end{matrix}\right.\)

Vậy: Vận tốc lúc đầu của người đó là 36km/h

a: ΔABC vuông cân tại A

mà AM là đường trung tuyến

nên AM là phân giác của góc BAC

=>\(\widehat{BAM}=\widehat{CAM}=\dfrac{90^0}{2}=45^0\)

Xét tứ giác ADME có \(\widehat{EMD}+\widehat{EAD}=90^0+90^0=180^0\)

nên ADME là tứ giác nội tiếp

=>\(\widehat{MAD}=\widehat{MED};\widehat{MDE}=\widehat{MAE}\)

mà \(\widehat{MAD}=\widehat{MAE}=45^0\)

nên \(\widehat{MED}=\widehat{MDE}=45^0\)

=>MD=ME

b: Kẻ DF\(\perp\)AB(F\(\in\)BC)

mà AC\(\perp\)AB

nên DF//AC

DF//AC

=>\(\widehat{DFB}=\widehat{ACB}\)

mà \(\widehat{ACB}=\widehat{ABC}\)

nên \(\widehat{DFB}=\widehat{FBD}\)

=>ΔDFB cân tại D

=>DF=DB

mà DB=CK

nên DF=CK

Xét tứ giác DFKC có

DF//CK

DF=CK

Do đó: DFKC là hình bình hành

=>DK cắt FC tại trung điểm của mỗi đường

=>I là trung điểm chung của DK và FC