Cho \(\overline{abc+def}⋮37.\) Chứng minh \(\overline{abcdef⋮37}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔMAE và ΔMDB có
MA=MD
\(\widehat{AME}=\widehat{DMB}\)(hai góc đối đỉnh)
ME=MB
Do đó: ΔMAE=ΔMDB
=>AE=BD
b: Xét ΔABC có \(\widehat{ACB}< \widehat{ABC}\)
mà AB,AC lần lượt là cạnh đối diện của các góc ACB,ABC
nên AB<AC
Xét ΔABC có AB<AC
mà BD,CD lần lượt là hình chiếu của AB,AC trên BC
nên BD<CD
c: Xét ΔMAF và ΔMDC có
MA=MD
\(\widehat{AMF}=\widehat{DMC}\)(hai góc đối đỉnh)
MF=MC
Do đó: ΔMAF=ΔMDC
=>\(\widehat{MAF}=\widehat{MDC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AF//DC
=>AF//BC
Ta có: ΔMAE=ΔMDB
=>\(\widehat{MAE}=\widehat{MDB}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AE//BD
=>AE//BC
Ta có: AE//BC
AF//BC
AE,AF có điểm chung là A
Do đó: E,A,F thẳng hàng

Bổ sung đề; MB\(\perp\)OB tại B
a: Xét ΔOAM vuông tại A và ΔOBM vuông tại B có
OM chung
\(\widehat{AOM}=\widehat{BOM}\)(OM là phân giác của góc AOB)
Do đó: ΔOAM=ΔOBM
=>MA=MB
b: Ta có: ΔOAM=ΔOBM
=>OA=OB
=>ΔOAB cân tại O
c: Xét ΔMAD vuông tại A và ΔMBE vuông tại B có
MA=MB
\(\widehat{AMD}=\widehat{BME}\)(hai góc đối đỉnh)
Do đó: ΔMAD=ΔMBE
=>MD=ME

Viết bài văn nghị luận về vấn đề học sinh hút thuốc lá
Thuốc lá điện tử đang trở thành một hiện tượng phổ biến ở Việt Nam, đặc biệt là trong giới trẻ. Theo số liệu năm 2020, tỷ lệ sử dụng thuốc lá điện tử ở nam giới trưởng thành là 5,6%, còn ở nữ giới là 1%. Nghiên cứu tại Hà Nội năm 2020 cũng chỉ ra rằng tỷ lệ hút thuốc lá điện tử ở học sinh lớp 8-12 là 8,35% (nam 12,39%, nữ 4,8%). Thói quen này không chỉ ảnh hưởng đến sức khỏe cá nhân mà còn gây nguy hiểm cho tương lai của thế hệ trẻ.
Hiện nay, việc hút thuốc lá điện tử đã trở nên quá phổ biến, đặc biệt là trong giới trẻ. Sức khỏe của những người sử dụng thuốc lá điện tử đang bị đe dọa bởi những hậu quả nặng nề của chính thói quen này. Nicotin, chất có trong thuốc lá điện tử, cùng với các chất độc hại khác đang tạo nên một vấn đề sức khỏe công cộng ngày càng trầm trọng. Điều này đặt ra câu hỏi lớn về ý thức và trách nhiệm của từng cá nhân trong việc ngăn chặn lan truyền của thói quen nguy hại này.Để giảm thiểu tác động tiêu cực của thuốc lá điện tử, chúng ta cần tăng cường công tác tuyên truyền và giáo dục về tác hại của nó. Người dân, đặc biệt là giới trẻ và học sinh, cần được thông tin đầy đủ về những nguy cơ và hậu quả của việc sử dụng thuốc lá điện tử. Ngoài ra, việc xử lý nghiêm những trường hợp hút thuốc lá điện tử ở nơi công cộng là một biện pháp cần thiết để ngăn chặn sự lan truyền của thói quen này. Mỗi cá nhân cần nhận thức được vai trò quan trọng của bản thân trong việc bảo vệ sức khỏe cộng đồng.
Vấn đề của thuốc lá điện tử không chỉ là vấn đề cá nhân mà còn là vấn đề xã hội, đòi hỏi sự chung tay của toàn xã hội. Để xây dựng một môi trường sống lành mạnh và bảo vệ tương lai của thế hệ trẻ, chúng ta cần cùng nhau đối mặt và giải quyết hiệu quả vấn nạn này. Bằng sự tìm hiểu, nhận thức, và hành động đồng lòng, chúng ta có thể hạn chế tối đa tác động tiêu cực của thuốc lá điện tử và giữ gìn sức khỏe cho bản thân và cộng đồng.

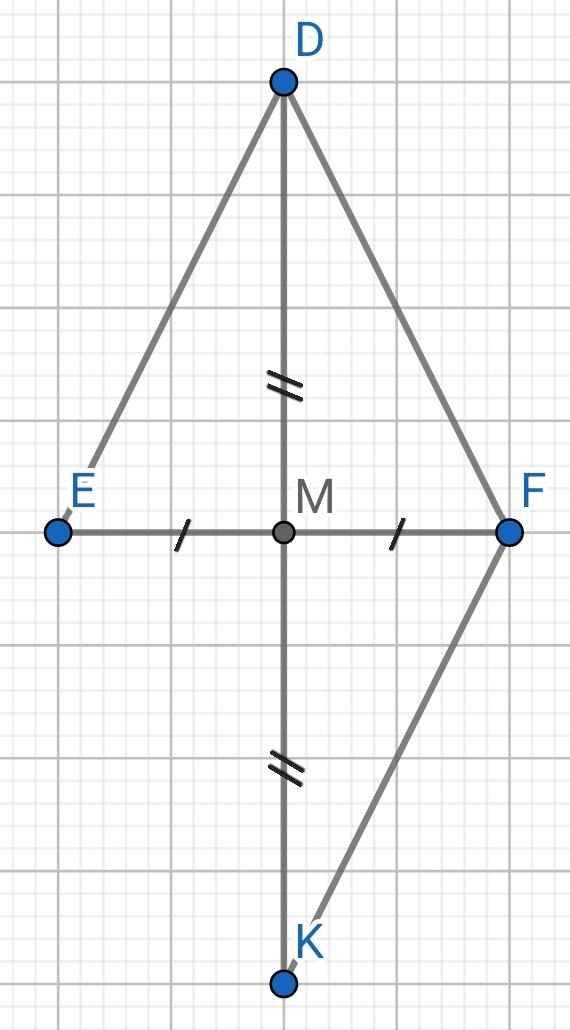
a) Do ∆DEF cân tại D (gt)
⇒ DE = DF
Do M là trung điểm của EF (gt)
⇒ ME = MF
Xét ∆DEM và ∆DFM có:
DE = DF (cmt)
DM là cạnh chung)
ME = MF (cmt)
⇒ ∆DEM = ∆DFM (c-c-c)
b) Sửa đề: Chứng minh DM ⊥ EF
Do ∆DEM = ∆DFM (cmt)
⇒ ∠DME = ∠DMF (hai góc tương ứng)
Mà ∠DME + ∠DMF = 180⁰ (kề bù)
⇒ ∠DME = ∠DMF = 180⁰ : 2 = 90⁰
⇒ DM ⊥ EF
c) Xét ∆DEM và ∆KFM có:
DM = KM (gt)
∠DME = ∠KMF (đối đỉnh)
ME = MF (cmt)
⇒ ∆DEM = ∆KFM (c-g-c)
⇒ DE = KF (hai cạnh tương ứng)
Mà DE = DF (cmt)
⇒ KF = DF
⇒ ∆FDK cân tại F
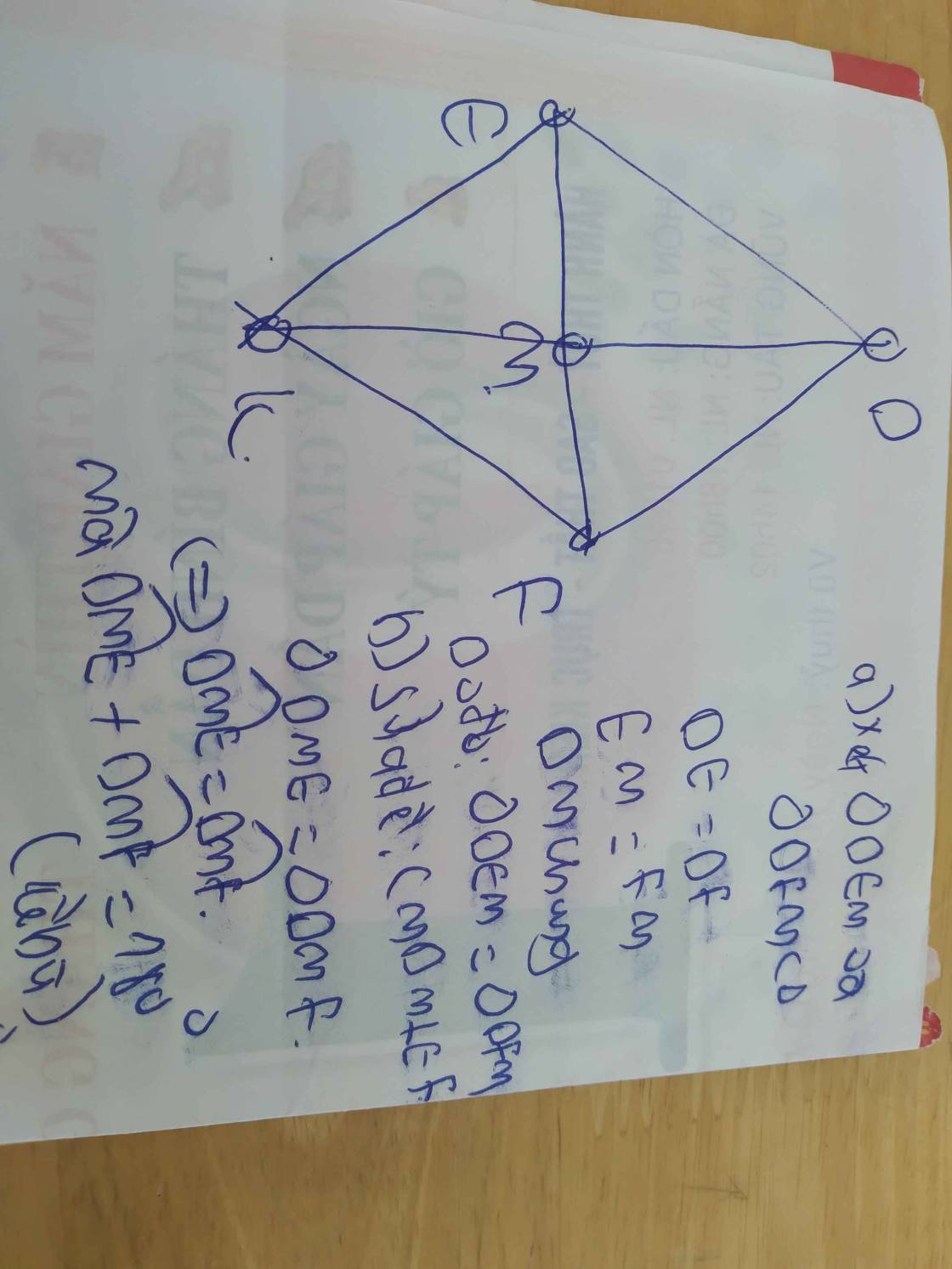
a) tìm ba số x,y,z biết x/3=y/4=z/5 và x.y.z=480
b) tìm ba số a,b,c biết a/4=b/8=c/16 và a^2-b^2=-60

a) Ta có :
\(\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{z}{5}=k\)
\(\Rightarrow k^3=\dfrac{x}{3}.\dfrac{y}{4}.\dfrac{z}{5}=\dfrac{480}{3.4.5}=8\)
\(\Rightarrow k=2\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{x}{3}=2\\\dfrac{y}{4}=2\\\dfrac{z}{5}=2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=6\\y=8\\z=10\end{matrix}\right.\)
Vậy \(\left\{{}\begin{matrix}x=6\\y=8\\z=10\end{matrix}\right.\)
b) Ta có :
\(\dfrac{a}{4}=\dfrac{b}{8}=\dfrac{c}{16}\)
\(\Rightarrow\left(\dfrac{a}{4}\right)^2=\left(\dfrac{b}{8}\right)^2=\left(\dfrac{c}{16}\right)^2\)
\(\Rightarrow\dfrac{a^2}{16}=\dfrac{b^2}{64}=\dfrac{c^2}{256}\)
Áp dụng TCDTSBN, ta có :
\(\dfrac{a^2}{16}=\dfrac{b^2}{64}=\dfrac{c^2}{256}=\dfrac{a^2-b^2}{16-64}=\dfrac{-60}{-48}=\dfrac{5}{4}\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{a^2}{16}=\dfrac{5}{4}\\\dfrac{b^2}{64}=\dfrac{5}{4}\\\dfrac{c^2}{256}=\dfrac{5}{4}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a^2=4.5\\b^2=16.5\\c^2=256.5\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}a=\pm2\sqrt[]{5}\\b=\pm4\sqrt[]{5}\\c=\pm16\sqrt[]{5}\end{matrix}\right.\)
Vậy \(\left\{{}\begin{matrix}a=\pm2\sqrt[]{5}\\b=\pm4\sqrt[]{5}\\c=\pm16\sqrt[]{5}\end{matrix}\right.\)

a) Áp dụng TCDTSBN, ta có :
\(\dfrac{x}{1}=\dfrac{y}{2}=\dfrac{z}{4}=\dfrac{2x-4y+z}{1.2-4.2+4}=\dfrac{-6}{-2}=3\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{x}{1}=3\\\dfrac{y}{2}=3\\\dfrac{z}{4}=3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=3\\y=6\\z=12\end{matrix}\right.\)
Vậy \(\left\{{}\begin{matrix}x=3\\y=6\\z=12\end{matrix}\right.\)
b) Áp dụng TCDTSBN, ta có :
\(\dfrac{a}{2}=\dfrac{b}{-4}=\dfrac{c}{6}=\dfrac{a-5b+4c}{2-5.\left(-4\right)+4.6}=\dfrac{23}{46}=\dfrac{1}{2}\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{a}{2}=\dfrac{1}{2}\\\dfrac{b}{-4}=\dfrac{1}{2}\\\dfrac{c}{4}=\dfrac{1}{2}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=1\\b=-2\\c=2\end{matrix}\right.\)
Vậy \(\left\{{}\begin{matrix}a=1\\b=-2\\c=2\end{matrix}\right.\)

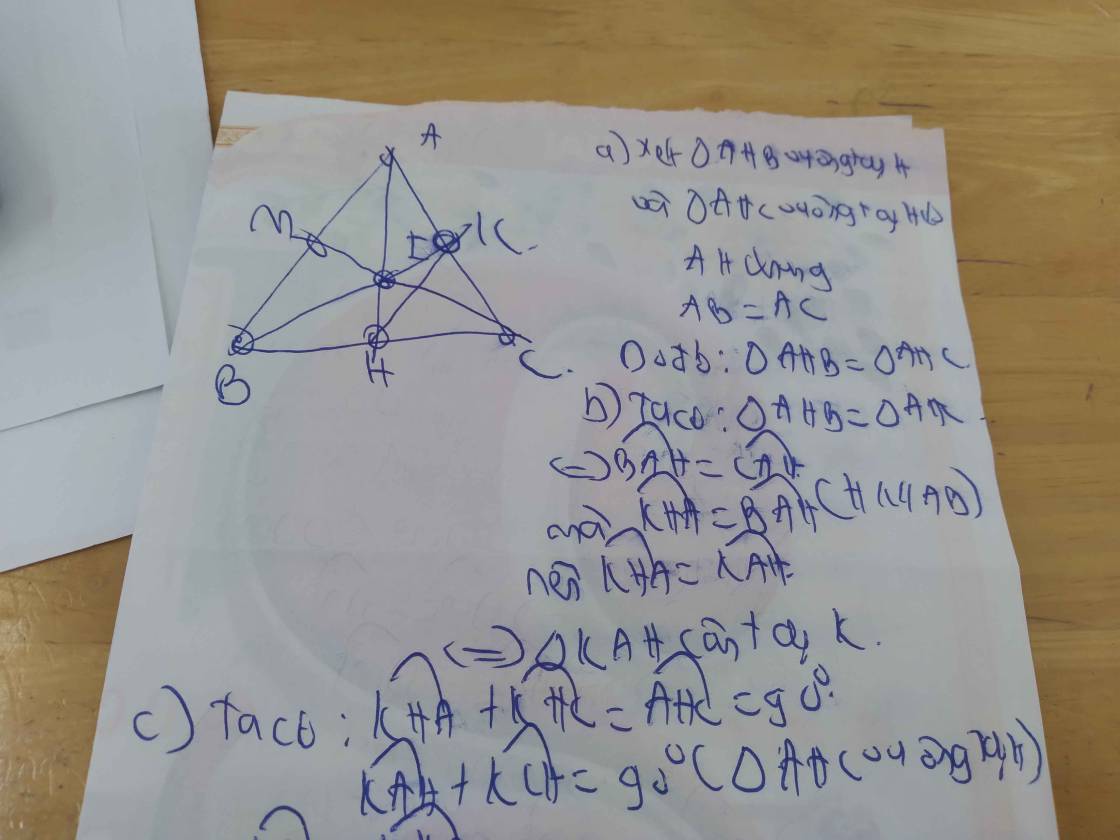
a/
Xét tg vuông AHB và tg vuông AHC có
AB = AC (cạnh bên tg cân)
HB = HC (trong tg cân đường cao hạ từ đỉnh tg cân đồng thời là đường trung tuyến)
=> tg AHB = tg AHC (Hai tg vuông có cạnh huyền và cạnh góc vuông tương ứng bằng nhau)
b/
Xét tg ABC có
HB = HC (cmt); HK//AB (gt) => KA=KC (trong tg đường thẳng đi qua trung điểm của 1 cạnh và // với 1 cạnh thì đi qua trung điểm cạnh còn lại)
Xét tg vuông AHC có
KA=KC (cmt)
\(\Rightarrow HK=KA=KC=\dfrac{AC}{2}\) (trong tg vuông trung tuyến thuộc cạnh huyền bằng nửa cạnh huyền)
=> tg AHK cân tại K
c/
Xét tg vuông ABC có
HB=HC (cmt); KA=KC (cmt) => I là trọng tâm của tg ABC
=> CI là trung uyến của tg ABC (trong tg 3 đường trung tuyến đồng quy) \(\Rightarrow M\in CI\) => C, I, M thẳng hàng

Kéo dài AM cắt BC tại A'.
Xét ΔABA' ta có BĐT: AB + BA' > AA' = MA + MA'
hay AB + BA' > MA + MA' (1)
Xét ΔCMA' ta có BĐT: CA' > MC - MA' (2) Cộng theo vế (1) và (2) ta được:
(AB + BA' ) + CA' > ( MA + MA' ) + ( MC - MA' ) <===> AB + (BA' + CA') > MA + MC
Hay: AB + CB > MA + MC (I) Chứng minh tương tự ta có:
AB + AC > MB + MC (II)
CB + AC > MA + MB (III) Cộng theo vế (I),(II) và (III) ta được:
2(AB+AC+CB) > 2(MA + MB + MC)
Hay: MA+MB+MC < AB+AC+CB (đpcm).

Số nguyên dương này không thể xác định vì số chữ số của số đó chưa xác định là bao nhiêu.

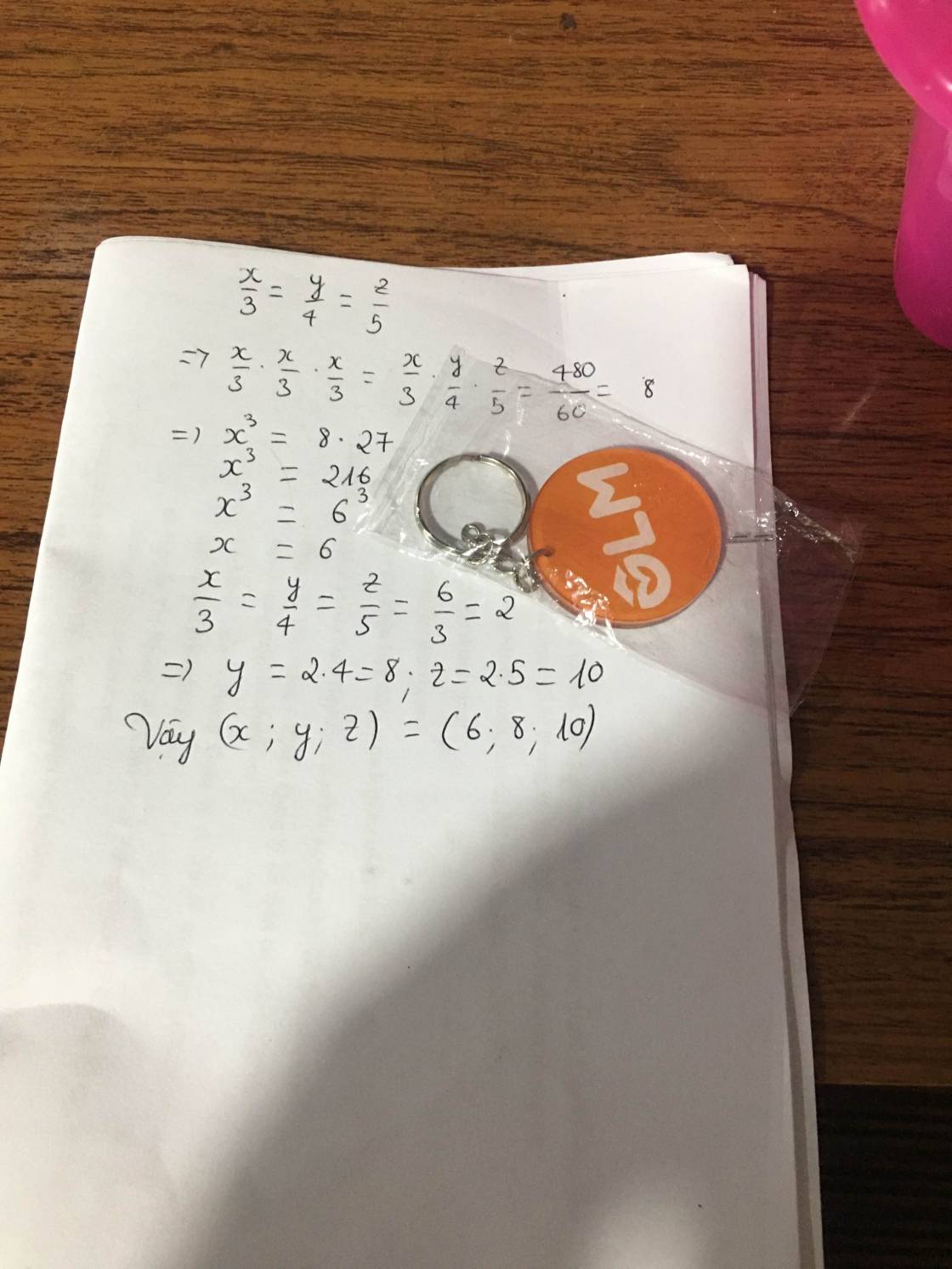


Ta có:
abcdef = 1000abc + def
Do (abc + def) ⋮ 37
Mà 37 là số nguyên tố
⇒ abc ⋮ 37 và def ⋮ 37
*) abc ⋮ 37
⇒ 1000abc ⋮ 37
⇒ (1000abc + def) ⋮ 37
⇒ abcdef ⋮ 37