K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NV
Nguyễn Việt Dũng
CTVVIP
1 tháng 5
- Về mặt quân sự:
+ Là chiến thắng quân sự oanh liệt: Chiến dịch Điện Biên Phủ là chiến dịch quy mô lớn nhất trong cuộc kháng chiến chống Pháp, với sự huy động lực lượng và nguồn lực to lớn của cả nước. Quân và dân ta đã dũng cảm chiến đấu, lập nên những chiến công vang dội, tiêu diệt hoàn toàn tập đoàn cứ điểm Điện Biên Phủ - "pháo đài không thể công phá" của thực dân Pháp.
+ Làm phá sản chiến lược Nava của Pháp: Chiến lược Nava của Pháp nhằm giành thắng lợi quân sự quyết định trong vòng 18 tháng (từ tháng 11/1953 đến tháng 4/1954) để buộc ta ký kết hiệp định hòa bình có lợi cho Pháp. Tuy nhiên, với chiến thắng Điện Biên Phủ, âm mưu của Pháp hoàn toàn bị phá sản, buộc chúng phải ký Hiệp định Genève, chấm dứt chiến tranh xâm lược Việt Nam.
- Về mặt chính trị:
+ Nâng cao uy tín quốc tế của Việt Nam: Chiến thắng Điện Biên Phủ khẳng định sức mạnh của dân tộc Việt Nam, buộc các nước đế quốc phải nhìn nhận Việt Nam là một quốc gia độc lập, tự chủ.
+ Góp phần thúc đẩy phong trào giải phóng dân tộc trên thế giới: Chiến thắng Điện Biên Phủ là nguồn cổ vũ to lớn cho các phong trào giải phóng dân tộc ở các nước thuộc địa, góp phần vào sự sụp đổ của hệ thống thuộc địa trên thế giới.
+ Tạo điều kiện thuận lợi cho việc thống nhất đất nước: Sau chiến thắng Điện Biên Phủ, miền Bắc hoàn toàn giải phóng, tạo điều kiện thuận lợi cho việc tiến lên giải phóng miền Nam, thống nhất đất nước.
2 tháng 5
a: ΔOBA cân tại O
mà OI là đường trung tuyến
nên OI\(\perp\)AB tại I
Ta có: \(\widehat{OIM}=\widehat{OCM}=\widehat{ODM}=90^0\)
=>O,I,C,M,D cùng thuộc đường tròn đường kính OM
b: Xét (O) có
MC,MD là các tiếp tuyến
Do đó: MC=MD
=>M nằm trên đường trung trực của CD(1)
Ta có: OC=OD
=>O nằm trên đường trung trực của CD(2)
Từ (1),(2) suy ra OM là đường trung trực của CD
=>OM\(\perp\)CD tại H và H là trung điểm của CD
Xét ΔEOM có
MI,EH là các đường cao
MI cắt EH tại S
Do đó: S là trực tâm của ΔEOM
=>OS\(\perp\)EM
2 tháng 5
bài 1:
a: \(\left\{{}\begin{matrix}3x+2y=5\\2x+y=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3x+2y=5\\4x+2y=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-x=1\\2x+y=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-1\\y=2-2x=2-2\cdot\left(-1\right)=4\end{matrix}\right.\)
b: Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=5\\x_1x_2=\dfrac{c}{a}=2\end{matrix}\right.\)
\(A=x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2\)
\(=5^2-2\cdot2=25-4=21\)
1 tháng 5
a: Xét (O) có
ΔBAC nội tiếp
BC là đường kính
Do đó: ΔBAC vuông tại A
=>PA\(\perp\)BD tại A
Xét (O) có
ΔCIB nội tiếp
CB là đường kính
Do đó: ΔCIB vuông tại I
Xét tứ giác ADHC có \(\widehat{DAC}+\widehat{DHC}=90^0+90^0=180^0\)
nên ADHC là tứ giác nội tiếp
b: Xét ΔDBP có
PA,BH là các đường cao
PA cắt BH tại C
Do đó: C là trực tâm của ΔDBP
=>DC\(\perp\)BP
mà CI\(\perp\)BP
mà DC,CI có điểm chung là C
nên D,C,I thẳng hàng
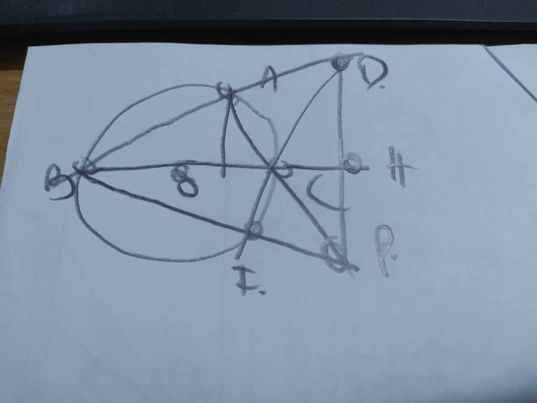
| GT | (O) có đường kính BC \(A\in\left(O\right);AP>AC;P\in AC\) PB\(\cap\)(O)={I} PH\(\perp\)BC tại H, PH cắt BA tại D |
| KL | a: ACHD nội tiếp b: D,C,I thẳng hàng |
KV
1 tháng 5
Câu 1
∆' = [-(m + 1)]² - m(m + 2)
= m² + 2m + 1 - m² - 2m
= 1 > 0
Phương trình luôn có hai nghiệm phân biệt
Theo hệ thức Vi-ét, ta có:
x₁ + x₂ = 2(m + 1)/m
x₁x₂ = (m + 2)/m
KV
1 tháng 5
Câu 3:
∆' = 4 - (2 - √3)(2 + √2)
= 4 - 4 - 2√2 + 2√3 + √6
= √6 + 2√3 - 2√2 > 0
Phương trình luôn có hai nghiệm phân biệt
Theo hệ thức Vi-ét, ta có:
x₁ + x₂ = -4/(2 - √3)= -8 - 2√3
x₁x₂ = (2 + √2)/(2 - √3) = (2 + √2)(2 + √3)