Ta có: \(2x=3y=5z\Rightarrow\dfrac{x}{\dfrac{1}{2}}=\dfrac{y}{\dfrac{1}{3}}=\dfrac{z}{\dfrac{1}{5}}\)

Áp dụng tính chất của dãy tỉ số bằng nhau và \(x-2y+z=14\), ta được:

\(\dfrac{x}{\dfrac{1}{2}}=\dfrac{y}{\dfrac{1}{3}}=\dfrac{2y}{\dfrac{2}{3}}=\dfrac{z}{\dfrac{1}{5}}=\dfrac{x-2y+z}{\dfrac{1}{2}-\dfrac{2}{3}+\dfrac{1}{5}}=\dfrac{14}{\dfrac{1}{30}}=420\)

\(\Rightarrow\left\{{}\begin{matrix}x=420\cdot\dfrac{1}{2}=210\\y=420\cdot\dfrac{1}{3}=140\\z=420\cdot\dfrac{1}{5}=84\end{matrix}\right.\)

$\text{#}Toru$

\(2x=3y=5z\Rightarrow\dfrac{2x}{30}=\dfrac{3y}{30}=\dfrac{5z}{30}=\dfrac{x}{15}=\dfrac{y}{10}=\dfrac{z}{6}\)

Áp dụng t/c dãy tỉ số bằng nhau:

\(\dfrac{x}{15}=\dfrac{y}{10}=\dfrac{z}{6}=\dfrac{x}{15}=\dfrac{2y}{20}=\dfrac{z}{6}=\dfrac{x-2y+z}{15-20+6}=\dfrac{14}{1}=14\)

\(\Rightarrow\left\{{}\begin{matrix}x=15.14=210\\y=10.14=140\\z=6.14=84\end{matrix}\right.\)

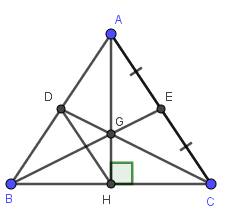
a) Do \(\Delta ABC\) cân tại A (gt)

\(\Rightarrow AB=AC\)

Xét hai tam giác vuông: \(\Delta AHB\) và \(\Delta AHC\) có:

\(AB=AC\left(cmt\right)\)

\(AH\) là cạnh chung

\(\Rightarrow\Delta AHB=\Delta AHC\) (cạnh huyền - cạnh góc vuông)

b) \(\Delta ABC\) cân tại A (gt)

\(AH\) là đường cao của \(\Delta ABC\) (gt)

\(\Rightarrow AH\) cũng là đường phân giác, đường trung tuyến của \(\Delta ABC\)

\(\Rightarrow\widehat{BAH}=\widehat{CAH}\)

\(\Rightarrow\widehat{DAH}=\widehat{HAC}\)

Do \(HD\) // \(AC\) (gt)

\(\Rightarrow\widehat{AHD}=\widehat{HAC}\)

Mà \(\widehat{DAH}=\widehat{HAC}\left(cmt\right)\)

\(\Rightarrow\widehat{AHD}=\widehat{DAH}\)

\(\Rightarrow\Delta AHD\) cân tại D

\(\Rightarrow AD=DH\)

c) Do \(\Delta ABC\) cân tại A (gt)

\(\Rightarrow\widehat{ABC}=\widehat{ACB}\)

\(\Rightarrow\widehat{DBH}=\widehat{ACB}\)

Do \(HD\) // \(AC\) (gt)

\(\Rightarrow\widehat{DHB}=\widehat{ACB}\) (đồng vị)

Mà \(\widehat{DBH}=\widehat{ACB}\left(cmt\right)\)

\(\Rightarrow\widehat{DHB}=\widehat{DBH}\)

\(\Rightarrow\Delta BHD\) cân tại D

\(\Rightarrow DH=BD\)

Mà \(DH=AD\left(cmt\right)\)

\(\Rightarrow AD=BD\)

\(\Rightarrow D\) là trung điểm của AB

\(\Rightarrow CD\) là đường trung tuyến của \(\Delta ABC\)

Lại có \(AH\) là đường trung tuyến của \(\Delta ABC\)

\(\Rightarrow G\) là trọng tâm của \(\Delta ABC\)

Do \(E\) là trung điểm của AC (gt)

\(\Rightarrow BE\) là đường trung tuyến của \(\Delta ABC\)

Mà \(G\) là trọng tâm của \(\Delta ABC\) (cmt)

\(\Rightarrow B,G,E\) thẳng hàng

\(\Rightarrow AH\) cũng là đường trung tuyến

\(2x^3-4x^2+3x+a-10=2x^3-4x^2+3x-6+a-4\)

\(=\left(2x^3-4x^2\right)+\left(3x-6\right)+a-4\)

\(=2x^2\left(x-2\right)+3\left(x-2\right)+a-4\)

\(\Rightarrow\left(2x^3-4x^2+3x+a-10\right):\left(x-2\right)\)

\(=\left[2x^2\left(x-2\right)+3\left(x-2\right)+a-4\right]:\left(x-2\right)\)

\(=2x^2+3+\dfrac{a-4}{x-2}\)

Để đa thức đã cho chia hết cho \(x-2\) thì \(a-4=0\)

\(\Rightarrow a=4\)

a: Sửa đề; MF vuông góc với AC tại F

Xét ΔBEM vuông tại E và ΔCFM vuông tại F có

BM=CM

\(\widehat{MBE}=\widehat{MCF}\)

Do đó: ΔBEM=ΔCFM

b: Ta có: ΔBEM=ΔCFM

=>ME=MF

=>M nằm trên đường trung trực của EF(1)

ta có: ΔBEM=ΔCFM

=>BE=CF

Ta có: AE+EB=AB

AF+FC=AC

mà BE=FC và AB=AC

nên AE=AF

=>A nằm trên đường trung trực của EF(2)

Từ (1),(2) suy ra AM là đường trung trực của EF

c: Xét ΔABC có \(\dfrac{AE}{AB}=\dfrac{AF}{AC}\)

nên EF//BC

d: Xét ΔABD vuông tại B và ΔACD vuông tại C có

AD chung

AB=AC

Do đó: ΔABD=ΔACD

=>DB=DC

=>D nằm trên đường trung trực của BC(3)

ta có: AB=AC

=>A nằm trên đường trung trực của BC(4)

ta có: MB=MC

=>M nằm trên đường trung trực của BC(5)

Từ (3),(4),(5) suy ra A,M,D thẳng hàng

a: Xét ΔBAD vuông tại A và ΔBHD vuông tại H có

BD chung

\(\widehat{ABD}=\widehat{HBD}\)

Do đó: ΔBAD=ΔBHD

b: ΔBAD=ΔBHD

=>DA=DH

Xét ΔDAK vuông tại A và ΔDHC vuông tại H có

DA=DH

AK=HC

Do đó: ΔDAK=ΔDHC

=>\(\widehat{ADK}=\widehat{HDC}\)

=>\(\widehat{ADK}+\widehat{ADH}=180^0\)

=>K,D,H thẳng hàng

a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có

AB=AC

\(\widehat{BAD}\) chung

Do đó: ΔADB=ΔAEC

b: Xét ΔCDB vuông tại D và ΔCDK vuông tại D có

CD chung

DB=DK

Do đó: ΔCDB=ΔCDK

=>CB=CK

=>ΔCBK cân tại C

c:

Ta có: ΔADB=ΔAEC
=>AD=AE

Xét ΔABC có \(\dfrac{AE}{AB}=\dfrac{AD}{AC}\)

nên ED//BC

=>\(\widehat{EDB}=\widehat{DBC}\)

=>\(\widehat{EDB}=\widehat{DKC}\)

a: Xét ΔABD vuông tại A và ΔEBD vuông tại E có

BD chung

\(\widehat{ABD}=\widehat{EBD}\)

Do đó: ΔABD=ΔEBD

b: Ta có: AH\(\perp\)BC

DE\(\perp\)BC

Do đó: AH//DE
Ta có: \(\widehat{BIH}+\widehat{HBI}=90^0\)(ΔHBI vuông tại H)

\(\widehat{ADI}+\widehat{ABD}=90^0\)(ΔABD vuông tại A)

mà \(\widehat{HBI}=\widehat{ABD}\)

nên \(\widehat{BIH}=\widehat{ADI}\)

=>\(\widehat{ADI}=\widehat{AID}\)

=>ΔAID cân tại A

c: Ta có: \(\widehat{CAE}+\widehat{BAE}=\widehat{BAC}=90^0\)

\(\widehat{HAE}+\widehat{BEA}=90^0\)

mà \(\widehat{BAE}=\widehat{BEA}\)(ΔBAE cân tại B)

nên \(\widehat{CAE}=\widehat{HAE}\)

=>AE là phân giác của góc HAC

\(4x^3-x^2-ax+b⋮x^2+1\)

=>\(4x^3+4x-x^2-1+\left(-a-4\right)x+b+1⋮x^2+1\)

=>-a-4=0 và b+1=0

=>a=-4 và b=-1

a: ΔABC vuông tại A

=>\(\widehat{ABC}+\widehat{ACB}=90^0\)

=>\(\widehat{ABC}=90^0-30^0=60^0\)

Xét ΔBAD có BA=BD và \(\widehat{ABD}=60^0\)

nên ΔBAD đều

b: Xét ΔBAE vuông tại A và ΔBDE vuông tại D có

BE chung

BA=BD

Do đó: ΔBAE=ΔBDE

=>\(\widehat{ABE}=\widehat{DBE}\)

=>BE là phân giác của góc ABC

c: Ta có: \(\widehat{DAC}+\widehat{DAB}=\widehat{BAC}\)

=>\(\widehat{DAC}+60^0=90^0\)

=>\(\widehat{DAC}=30^0\)

Xét ΔDAC có \(\widehat{DAC}=\widehat{DCA}\left(=30^0\right)\)

nên ΔDAC đều

=>DA=DC

=>DC=DB

=>D là trung điểm của BC

=>\(AD=\dfrac{1}{2}BC\)

d: Xét ΔBMC có

BN,CA là các đường cao

BN cắt CA tại E

Do đó: E là trực tâm của ΔBMC

=>ME\(\perp\)BC

mà ED\(\perp\)BC

nên M,E,D thẳng hàng

=>BA,CN,DE đồng quy

mọi ng giúp e nhanh với, e cảm ơn rất nhiềuuu

a: Xét ΔABM và ΔACM có

AB=AC

BM=CM

AM chung

Do đó: ΔAMB=ΔAMC

b: ΔAMB=ΔAMC

=>\(\widehat{MAB}=\widehat{MAC}\)

Xét ΔAEM vuông tại E và ΔAFM vuông tại F có

AM chung

\(\widehat{EAM}=\widehat{FAM}\)

Do đó: ΔAEM=ΔAFM

=>AE=AF và ME=MF

ta có: AE=AF

=>A nằm trên đường trung trực của EF(1)

Ta có: ME=MF

=>M nằm trên đường trung trực của EF(2)

Từ (1),(2) suy ra AM là đường trung trực của EF