Cho Tam giác ABC cân tại A lấy M trên BC sao cho MẸ vuông góc AB MF vuông góc ÁC trên FM lấy D sao cho MD = ME cm a góc BME = CMF b BD vuông góc với MD
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

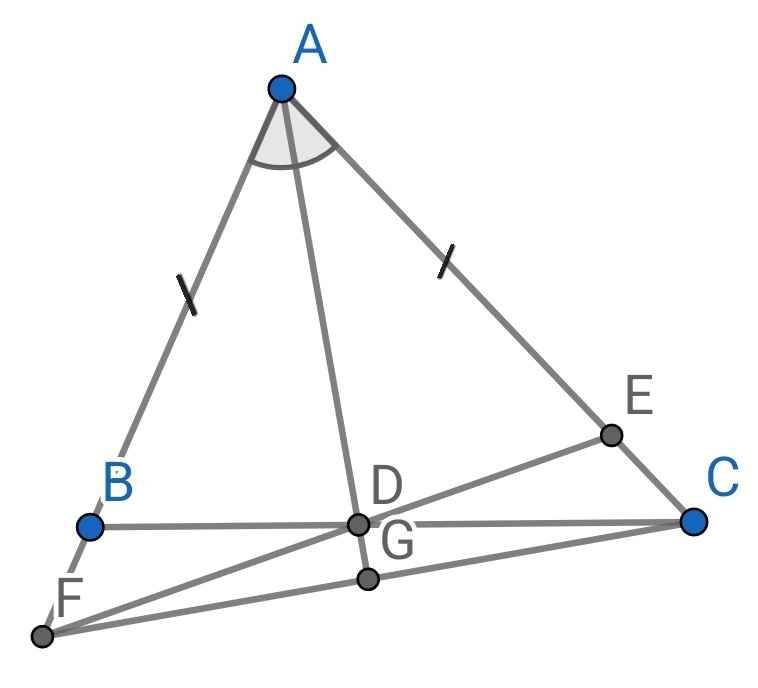 a) Do AD là tia phân giác của ∠BAC (gt)
a) Do AD là tia phân giác của ∠BAC (gt)
⇒ ∠BAD = ∠CAD
⇒ ∠BAD = ∠EAD
Xét ∆ABD và ∆AED có:
AD là cạnh chung
∠BAD = ∠EAD (cmt)
AB = AE (gt)
⇒ ∆ABD = ∆AED (c-g-c)
⇒ BD = ED (hai cạnh tương ứng)
Do ∆ABD = ∆AED (cmt)
⇒ ∠ABD = ∠AED (hai góc tương ứng)
Ta có:
∠ABD + ∠FBD = 180⁰ (kề bù)
∠AED + ∠CED = 180⁰ (kề bù)
Mà ∠ABD = ∠AED (cmt)
⇒ ∠FBD = ∠CED
Xét ∆BDF và ∆EDC có:
BD = ED (cmt)
∠FBD = ∠CED (cmt)
∠BDF = ∠EDC (đối đỉnh)
⇒ ∆BDF = ∆EDC (g-c-g)
b) Do ∆BDF = ∆EDC (cmt)
⇒ BF = EC (hai cạnh tương ứng)
c) Gọi G là giao điểm của AD và CF
AG là tia phân giác của ∠FAC
⇒ ∠FAG = ∠CAG
Xét ∆AFG và ∆ACG có:
AF = AC (gt)
∠FAG = ∠CAG (cmt)
AG là cạnh chung
⇒ ∆AFG = ∆ACG (c-c-c)
⇒ ∠AGF = ∠AGC (hai góc tương ứng)
Mà ∠AGF + ∠AGC = 180⁰ (kề bù)
⇒ ∠AGF = ∠AGC = 180⁰ : 2 = 90⁰
⇒ AG FC
Hay AD ⊥ FC

Lời giải:
Kẻ $Et\parallel a\parallel b$. Ta có:
$\widehat{E_1}=\widehat{A_1}=60^0$ (2 góc đồng vị)
$\widehat{E_2}=\widehat{K_1}=47^0$ (2 góc đồng vị)
$\Rightarrow \widehat{AEK}=\widehat{E_1}+\widehat{E_2}=60^0+47^0=107^0$

a, Vì góc dNm và góc HdN ở vị trí so le trong và bằng nhau nên
m//n.
b, \(\widehat{nHt}\) = 1800 - 550 = 1250
\(\widehat{HKN}\) = \(\widehat{nHt}\) = 1250 (hai góc đồng vị)
 bài của cô đúng rồi nhưng cho em hỏi là em làm theo cách này có đúng không nhé
bài của cô đúng rồi nhưng cho em hỏi là em làm theo cách này có đúng không nhé
Vì góc PHK và HKN là 2 góc bù nhau
Suy ra PHK +HKN =180 độ
PHK =180 độ - 55 độ có đúng không ạ nếu sai gì cô góp ý giúp em nhé

52x-3-2.52 =52 . 3
⇔52x-1.52-2.52=52.3
⇔52.(52x-1-2)=52.3
⇔52x-1-2=3
⇔52x-1=5
⇔2x-1=1
⇔2x=2
⇔x=1
vay x=1

a, \(\dfrac{5}{3}\).(- \(\dfrac{6}{5}\) + \(x\)) - \(\dfrac{1}{4}\).(\(\dfrac{2}{3}\) - 1) = - \(\dfrac{3}{8}\)
- 2 + \(\dfrac{5}{3}\)\(x\) - \(\dfrac{1}{6}\) + \(\dfrac{1}{4}\) = - \(\dfrac{3}{8}\)
\(\dfrac{5}{3}\)\(x\) - \(\dfrac{23}{12}\) = -\(\dfrac{3}{8}\)
\(\dfrac{5}{3}\)\(x\) = - \(\dfrac{3}{8}\) + \(\dfrac{23}{12}\)
\(\dfrac{5}{3}\) \(x\) = \(\dfrac{37}{24}\)
\(x\) = \(\dfrac{37}{24}\) : \(\dfrac{5}{3}\)
\(x\) = \(\dfrac{37}{40}\)

Lời giải:
$\frac{5}{3}(-\frac{6}{5}+x)-\frac{1}{4}(\frac{2}{3}-1)=\frac{-3}{8}$
$-2+\frac{5}{3}x+\frac{1}{12}=\frac{-3}{8}$
$\frac{5}{3}x-\frac{23}{12}=\frac{-3}{8}$
$\frac{5}{3}x=\frac{23}{12}+\frac{-3}{8}=\frac{37}{24}$
$x=\frac{37}{24}: \frac{5}{3}=\frac{37}{40}$

A B C D E M N
1/ Xét tg ABC và tg DBE có
BA=BD (gt)
DE//AC (gt) \(\Rightarrow\widehat{BAC}=\widehat{BDE}\) (góc so le trong)
\(\widehat{ABC}=\widehat{DBE}\) (góc đối đỉnh)
=> tg ABC = tg DBE (g.c.g)
2/
Ta có tg ABC = tg DBE (cmt) => BC=BE
Xét tư giác ACDE có
BA=BD (gt); BC=BE (cmt) => ACDE là hình bình hành (Tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường là hbh)
=> AE//CD (cạnh đối hbh)
3/
Xét tg ADC có
MA=MC (gt); BA=BD (gt) => BM là đường trung bình của tg ADC
=> BM//CD
Xét tg ADE có
BA=BD (gt); NE=ND (gt) => BN là đường trung bình của tg ADE
=> BN//AE
Mà CD//AE (cạnh đối hbh)
=> BM//AE (cùng //CD)
\(\Rightarrow BN\equiv BM\) (từ 1 điểm ngoài đường thẳng cho trước chỉ dựng được duy nhất 1 đường thẳng // với đường thẳng đã cho)
=> M, B, N thẳng hàng

Chắc phải có thêm điều kiện x; y nguyên nữa chứ em?